基于动态内部主元分析和隐马尔科夫模型的动态过程故障检测与分类方法

董 洁,游培航,彭开香

(北京科技大学自动化学院,北京 100083;北京科技大学工业过程知识自动化教育部重点实验,北京 100083)

1 引言

随着生产过程的规模化发展,工业过程的复杂度不断增加,传统的控制方法不能迅速准确的对生产过程进行监测.因此,建立可靠的过程监测系统,快速有效的检测故障并进行故障分类,降低异常事故的发生显得至关重要.采用合适的故障检测与分类方法,来保证复杂工业系统的安全运行,已经成为过程控制领域的首要任务.

过程监测方法主要分为定性分析的方法和定量分析的方法[1].其中,定性分析方法又细分为图论方法、专家系统和定性仿真;定量分析方法又分为基于解析模型的方法和数据驱动的方法.由于生产过程的日益复杂,生产过程的机理模型难以获得,基于数据驱动的方法逐渐成为研究的热点.传统的基于数据驱动的方法主要是多变量统计,其中最典型的是偏最小二乘法(partial least squares,PLS)和主元分析法(principal component analysis,PCA)[2].PLS通过最大化输入输出数据的协方差构建回归模型,并构建T2,SPE控制限进行过程监测.PCA的主要思想是通过关系度不强的特征信号实现对原始过程数据的降维,将原始过程数据分为主元子空间和残差子空间,并构建T2,SPE控制限分别监测这两个空间,以此实现过程监测.然而,传统的数据驱动方法没有考虑数据在时间维度上的依赖关系,无法提取工业过程数据的动态关系,也无法确定测量变量之间的自相关和互相关关系.针对传统数据驱动方法无法对动态过程进行有效监测的问题,许多学者对PLS和PCA进行了改进.Ku等人[3]提出了动态主元分析(dynamic principal component analysis,DPCA)方法,该方法将原始数据按照一定的时间窗口堆叠,形成增广数据矩阵,然后利用PCA进行过程监测;这种方法无法给出动态成分间的相互关系,且随着时间窗口的增大,容易造成维数灾难.彭等人[4]利用动态全潜结构投影算法(total projection to latent structures,T-PLS)实现了对带钢热连轧的厚度监控.Li等人[5]提出了动态潜变量算法,该方法首先利用自回归PCA算法提取潜变量,使其自协方差最大;然后对潜变量建立向量自回归模型,以此表示动态关系.虽然该方法建立了潜变量间的动态关系,但在提取潜变量时,仅仅考虑潜变量一阶时间阶次的自协方差.作为改进,Li等人[6]提出了结构化的DPCA算法,首先定义目标函数为最大化滞后潜变量加权和的方差,然后对潜变量建立向量自回归模型.然而,这种方法的缺陷是其动态关系的向量自回归模型与目标函数不一致.因此,Dong等人[7]提出了动态内部主元分析(dynamic-inner principal component analysis,DiPCA),通过定义潜变量为向量自回归模型,算法的目标函数为最大化实际潜变量与自回归模型估计潜变量之间的协方差,使潜变量内部动态关系的自回归模型与目标函数中一致.由于所提取的潜变量含有大量动态特性,直接对其监测会产生很大的误报警率.故该算法是对自回归模型的估计误差建立PCA模型,并构建T2,SPE混合指标[8]进行动态过程监测.

在检测出故障后,判断其属于哪一类故障,以便后续处理也是至关重要的.故障分类就是通过不同类型的故障数据样本建立分类模型,当监测模型检测出故障后,将故障数据输入分类模型,判断此故障属于哪一类别.准确构建故障分类模型也是当前的研究热点.Hu等人[9]将泵的运行状态分为正常、早期气蚀和严重气蚀3类,并且用K近邻分类器实现了准确的分类.Kurukuru等人[10]通过训练径向基函数(radial basis function,RBF)神经网络实现了对光伏系统不同类型故障的分类.Almalki等人[11]利用基于事件签名的决策树分类算法成功分类出配电系统中配电线高阻抗故障、电缆绝缘层击穿故障和断路器故障.Yu等人[12]将智能群算法与支持向量机结合,对燃料电池系统的5种故障状态进行分类.Xu等人[13]将滚动轴承的正常和故障信号进行经验模态分解作为特征,输入基于粒子群优化的支持向量机模型,实现了对轴承的正常和故障状态分类.Sun等人[14]利用稀疏自动编码器提取感应电动机的数据特征,并将特征用于训练深度神经网络分类器,实现了对电机不同故障的分类.Zhong等人[15]提出了一种半监督的Fisher分类器,并将其用于工业过程的故障分类.该方法通过合并其他未标记的数据样本进行建模,改善了传统分类方法对小样本数据建模的不足.Lucke等人[16]针对工业过程故障数据与正常数据样本数不平衡的问题,提出一种K均值贝叶斯分类算法,并在TE数据上验证了该算法的有效性.针对工业过程数据的动态性问题,Li等人[17]指出,隐马尔科夫模型(hidden Markov model,HMM)非常适合于动态时间序列的建模,并且具有强大的模式分类能力,特别是对于信息丰富、非平稳性、重复性和再现性差的信号.同时,理论上HMM可以处理长随机序列.他们将快速傅立叶变换(fast fourier transform,FFT)、小波变换、频谱提取的特征输入HMM构建分类器模型.针对旋转机械中的加速和减速过程识别,取得了良好的效果.

本文针对DiPCA算法所提取的动态主元直接进行监测会产生较大误报率的问题,利用HMM能够有效对时间序列进行建模并且具有强大的模式分类能力的特点,提出了一种动态过程故障检测与分类的一体化框架.该框架首先利用DiPCA算法提取正常工况下测量数据的动态特征,并对正常工况下的动态特征数据建立HMM监测模型,实现对工业动态过程的故障检测;然后利用历史故障数据,建立基于HMM的故障分类模型,实现对不同故障的分类;最后利用田纳西-伊斯曼(Tennessee Eastman,TE)过程数据验证DiPCA-HMM动态过程监测及故障分类框架的有效性.

本文剩余部分结构如下:第2部分介绍动态内部主元分析与隐马尔科夫模型的原理;第3部分提出动态过程监测及故障分类框架;第4部分将所提框架应用于田纳西-伊斯曼化学工业过程进行仿真实验,并与DiPCA动态过程监测算法和SVM故障分类算法对比;第5部分给出结论.

2 理论背景

2.1 动态内部主元分析(DiPCA)

设xk为k时刻采集到的样本数据,rk为xk中提取的主元,w为负载向量:

为了提取出变量间的动态特征,引入阶次为s的自回归模型:

DiPCA算法的目标是确定样本数据之间的自相关和互相关关系,并给出动态关系的明确表示.因此DiPCA算法的目标函数就是最大化rk与间的协方差:

由此可知,w是最大特征值所对应的特征向量.由于w与β混合在一起,此最优问题无解析解.定义得分向量

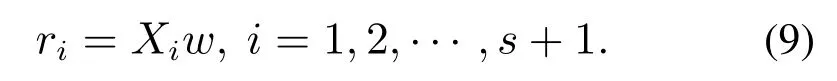
则式(8)表示为如下形式:

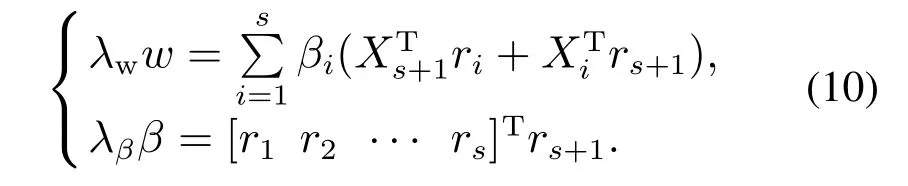
由式(10)可以得到β与ri的关系.因此,可以用迭代的方法求出此优化问题的解.DiPCA算法具体迭代过程如下:

1) 将X标准化为0均值,1方差,w初始化为随机单位向量;

2) 迭代以下步骤直至收敛:

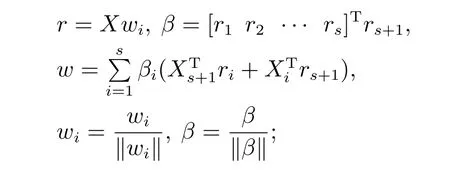
3)X=X -

4) 返回步骤2),提取下一个主元,直至提取出期望个数的主元;

5) 最终剩余的X可认为是数据的静态部分.

DiPCA算法需要确定主元个数l和自回归模型阶次s两个参数.首先假设s为确定值,则l可选择为包含95%自协方差的值,因此可将l看作关于s的函数l=l(s);然后根据交叉验证的方法确定s,首先通过一部分数据训练DiPCA模型,然后将此DiPCA模型作用于验证数据,得到数据的静态部分X,使X中任意两个变量间相关性最小的s即为最优.

2.2 隐马尔科夫(HMM)

HMM是一类基于概率统计的模型,它可以由5个部分表示:

1) 模型的隐状态.定义模型有N个隐状态,t时刻的隐状态表示qt ∈[S1··· SN];

2) 状态转移矩阵A={aij},其中

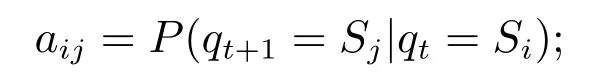
3) 观测值,即隐状态所有可能的输出值R={r1,r2,···,rM};

4) 观测概率分布矩阵B={bi(k)},其中bi(k)=P(rk|qt=Sj);

5) 初始隐状态分布π=P(q1=Si),1 ≤i≤N.

上述5个部分可以简化为λ=(A,B,π).根据观测值是离散或连续值,可以将HMM分为离散型HMM和连续型HMM两种.上述观测值为离散型HMM的观测值.对于连续性HMM,可以认为其隐状态输出符合混合高斯分布.

HMM主要解决以下3个问题:

1) 评估问题,即给定观察序列R={r1,r2,···,rT}和模型λ=(A,B,π),计算出现观察序列R的概率.这个问题可以通过定义前向或后向变量,采用动态规划算法进行求解.

2) 解码问题,即给定观察序列R={r1,r2,···,rT}和模型λ=(A,B,π),求出最可能的隐状态序列,这个问题可以用Viterbi算法进行求解.

3) 学习问题,即调整模型参数使观察到的序列出现可能性最大,这个问题可通过向前向后算法(Baum-Welch)求解,它是期望最大化算法(expectation maximization,EM)的一个特例,即带隐变量的最大似然估计问题.

在过程监测及故障分类框架中,对监测模型及分类模型的训练为学习问题,构造监测模型控制限以及求解分类模型输出概率为评估问题.因此,本文主要讨论3个问题中的学习问题和评估问题.

由于工业过程的隐状态输出一般为连续值,因此将观测值概率密度函数重新定义为B=[bi(r)],其分量为

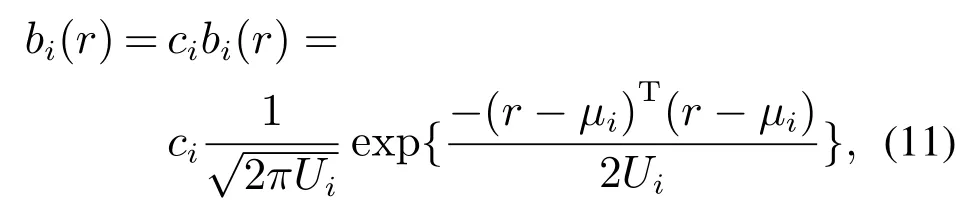
其中:i为t时刻的隐状态Si,r为t时刻的观测值,bi(r)为t时刻状态为Si时输出观测值为r的概率密度函数,采用高斯函数表示;µi,Ui分别为状态Si中高斯密度函数的均值向量和协方差矩阵.

采用前向-后向算法对HMM的学习问题进行求解,首先初始化模型中的所有参数.然后,定义前向概率αt(i)表示在t时刻处于状态i,且之前的观测序列为{r1,r2,···,rt}的概率,即

定义后向概率βt(i)表示已知t时刻处于状态i,之后的观测序列为{rt+1,···,rT}的概率,即

根据前向、后向概率递归计算,分别递归计算所有的αt(i),βt(i),假设SI为初始状态,SE为最终状态,表达式如下:

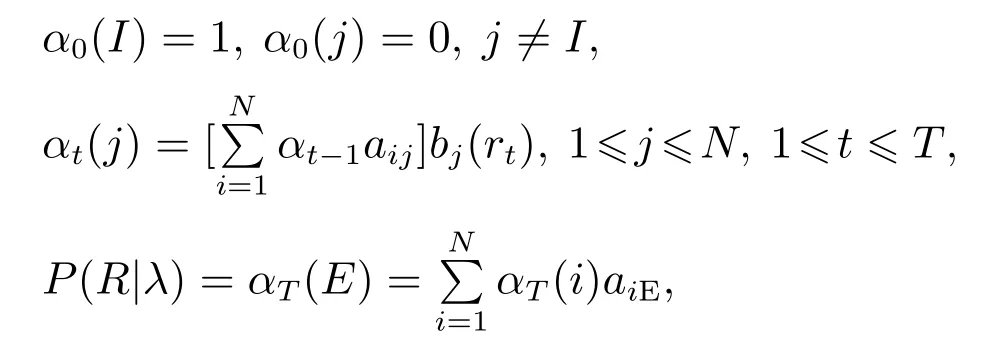
定义γt(j)为给定观测序列R和模型参数λ,t时刻处于状态i的概率:

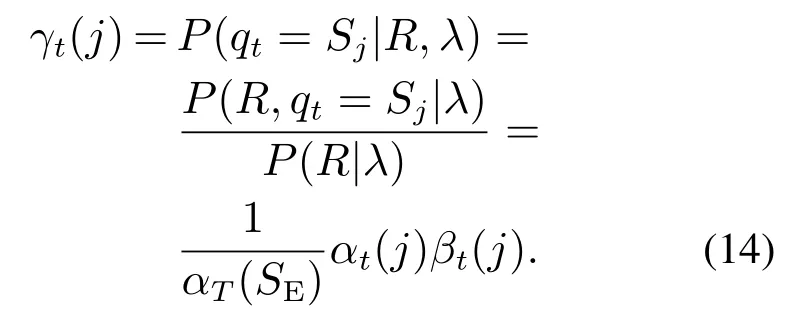
定义εt(i,j)为给定观察序列R和模型参数λ,在t时刻处于状态i,t+1时刻处于状态j的概率:

基于γt(j)和εt(i,j)重估HMM的初始状态概率、均值、方差和转移概率:

对于评估问题,由参数已知的HMM,可以求出给定观测值序列R由此HMM产生的概率:

3 基于DiPCA-HMM的动态过程故障检测及分类框架

3.1 DiPCA-HMM动态过程故障检测

设X ∈RN×m是过程中测量得到的N个m维正常工况数据.将X标准化,利用DiPCA算法提取其的动态特征,其中时间阶次为s.按照DiPCA算法流程中的步骤,迭代求出其动态主元:

对所提取的动态主元构建HMM模型,在训练阶段,需要解决HMM3个问题中的学习问题,即根据样本R训练出最优的模型参数λ=(A,B,π).

首先初始化模型参数λ,HMM模型的时间阶次与自回归模型时间阶次s一致;然后根据前向、后向概率递归计算αt(i)和βt(i),根据式(14)-(15)计算γt(j)和εt(i,j),接着通过式(16)-(19)对模型参数进行重新估计.重复上述过程直至式(22)收敛:

对cpi进行核密度估计,包含其密度函数99%区域的点定为控制限CP1.

在测试阶段,数据通过DiPCA算法提取出动态特征后,计算HMM输出概率的负对数似然值,通过与控制限进行比较,以此实现对动态过程的监测.DiPCAHMM动态过程监测框架如图1所示.

3.2 基于HMM的故障分类模型

被DiPCA-HMM动态过程监测框架检测出故障后,需要判断故障所属类型,以便后续进行有效处理,降低故障的影响.本文利用HMM具有强大的模式分类能力的特点,实现对不同故障的分类.离线建模阶段,利用历史K类故障数据分别建立K个HMM模型;在线监测阶段,当样本被DiPCA-HMM动态过程监测框架判定为故障时,将其分别输入K个HMM故障分类模型,比较每个HMM故障分类模型的输出概率,则此故障数据所属的故障类型认定为输出概率最大的HMM所属的类别.基于HMM的故障分类模型如图1所示.

4 TE过程实验仿真

田纳西-伊斯曼(TE)过程是美国Eastman化学公司依据实际化工反应过程开发的化工模型仿真平台,其产生的数据具有很强的动态特性,广泛应用于测试工业过程的控制和故障诊断模型.TE过程包含12个操纵变量和41个测量变量,测量变量中包含22个过程变量和19个质量变量.TE过程一共包含21种故障.其中,故障3,9,15由于控制系统的反馈调节对过程影响很小;故障16至故障21为未知类型故障.因此,本研究选取了22个过程变量XMEAS(1-22)和11个操纵变量XMV(1-11)组成原始数据集.选取12个故障作为对比验证集,如表1所示.在本文中,选取主元个数l=13,时间阶次s=3.基于DiPCA-HMM动态过程监测模型使用的数据集包含正常工况训练数据、正常工况测试数据和12种故障的测试数据;基于HMM的故障分类模型使用的数据集包含12种故障的训练数据和测试数据.其中,所有故障测试数据在第160样本点引入故障.

图1 DiPCA-HMM动态过程故障检测与分类一体化框架Fig.1 The integrated framework of dynamic fault detection and classification based on DiPCA-HMM

表1 故障类型Table 1 Fault type

利用正常工况下采集到的数据训练DiPCA-HMM动态过程监测框架,图2所示为DiPCA所提取的第1和第2个主元的自相关与互相关关系.其中,c11为第1个主元的自相关关系,c12为第1个主元与第2个主元之间的互相关关系,c22为第2个主元的自相关关系.由图2可以看出,DiPCA算法所提取的主元包含大量的动态信息.

图3-5分别为DiPCA算法与DiPCA-HMM框架对故障4,7,11监测结果对比图.图3-5中:图(a)为DiPCA监测结果,图(b)为DiPCA-HMM框架的监测结果.

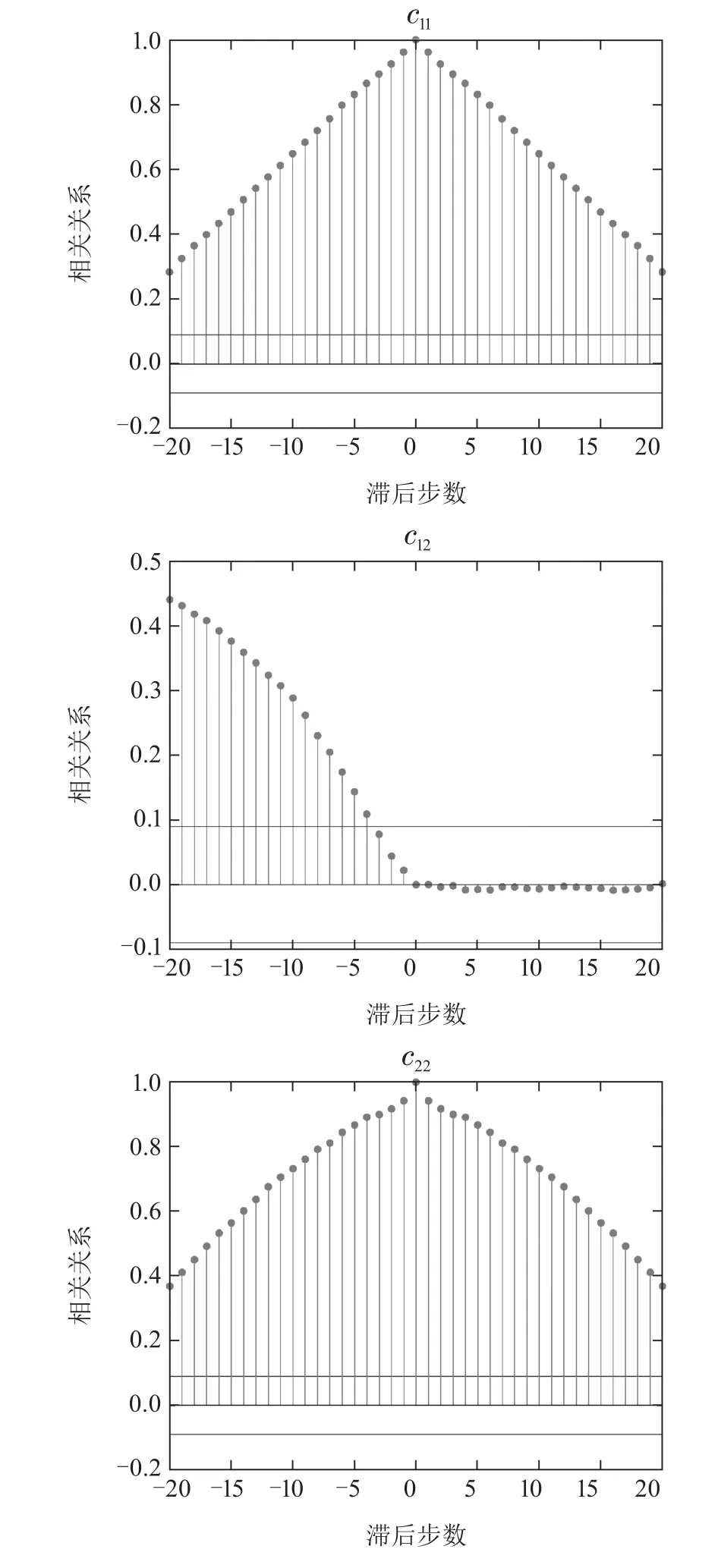
图2 动态主元间的自相关与互相关关系Fig.2 Autocorrelation and cross-correlation between dynamic principal components

图3 DiPCA与DiPCA-HMM故障4检测结果Fig.3 Fault detection result of DiPCA and DiPCA-HMM for Fault 4

由于DiPCA-HMM动态过程故障检测框架在对故障7的数据进行监测时,对于某些序列HMM的输出概率P为接近0的数值,其负对数似然值cp趋于正无穷,无法在图中标识,因此本文令其等于一个远大于控制限CP1的值.DiPCA与DiPCA-HMM对12种故障的检测率及误报率如表2所示.

图4 DiPCA与DiPCA-HMM故障7检测结果Fig.4 Fault detection result of DiPCA and DiPCA-HMM for Fault 7

图5 DiPCA与DiPCA-HMM故障11检测结果Fig.5 Fault detection result of DiPCA and DiPCA-HMM for Fault 11

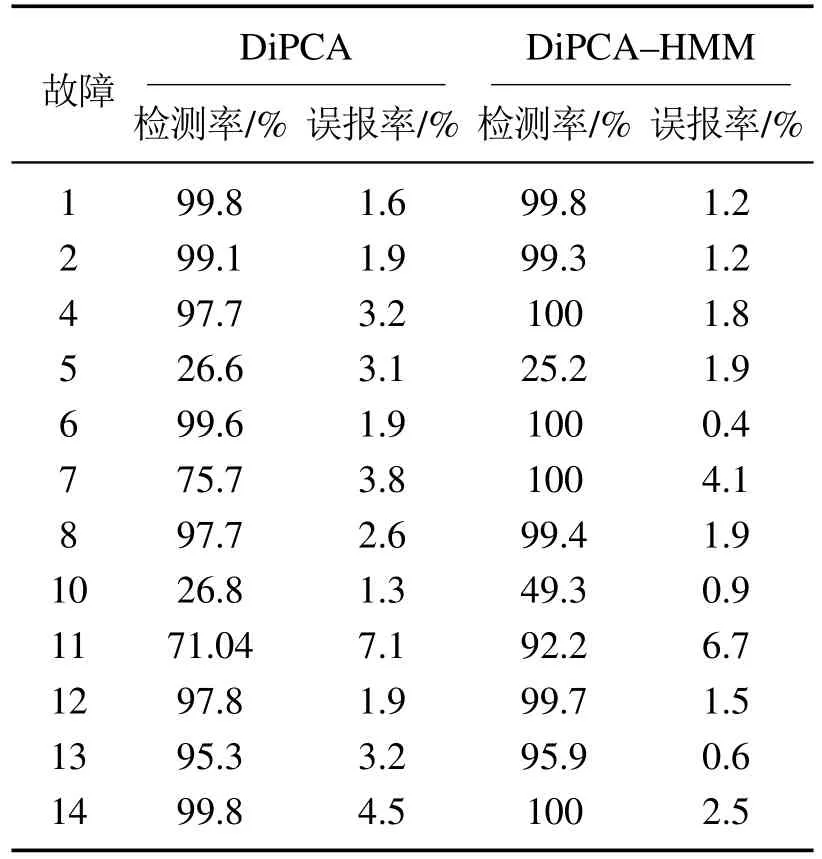
表2 故障检测率与误报率Table 2 Fault detection rate and alarm rate

表2中对于故障5和故障10,两种方法都没有实现准确的监测,而对两种故障数据的静态部分进行监测得到了较好的监测效果[7].可以认为,故障5和故障10所引起的数据变化主要表现在测量数据的静态部分.因此,对动态过程的监测无法准确有效的检测出这两种故障的发生.

表3所示为基于DiPCA-HMM的故障分类模型和一对一SVM分类器对所选的12个故障的分类准确率对比.第i类故障的故障分类准确率定义如下:

其中:Si为第i类故障样本总数,TSi为被正确分类为第i类故障的样本数.

表3 故障分类率Table 3 Fault classification rate

结果表明,对于故障5,6,8,11,13,HMM分类器效果优于SVM分类器.两种方法对故障10都无法准确有效的进行分类,其中SVM分类器将大部分故障10数据误判为故障12,而HMM分类器将大部分故障10数据误判为故障5.由于发生故障5与故障10时,数据的变化主要反应在静态部分,而所提取的动态特征相似性较高;因此,对它们的动态特征建立分类模型后,容易造成误判.

5 结论

本文提出一种基于DiPCA-HMM的动态过程故障检测与故障分类框架,该框架通过DiPCA算法提取正常工况数据的动态特征;然后利用HMM适合处理动态特征的特点进行故障检测,并根据负对数似然值构建监测控制限;最后对不同故障分别构建HMM模型,实现了对不同故障的分类.将DiPCA-HMM动态过程监测及故障分类框架应用于TE过程,选取12个故障进行仿真研究,结果表明,基于DiPCA-HMM的动态过程故障检测与分类框架能够有效的检测出故障,并实现故障分类.