锑浮选过程加药量自适应迭代学习控制

李中美 ,黄梦哲 ,桂卫华

(1.华东理工大学信息科学与工程学院,上海 200237;2.纽约大学工学院,美国纽约11201; 3.中南大学自动化学院,湖南长沙 410083)

1 引言

随着制造业的飞速发展,尤其在建设“一带一路”,建立全球矿业命运共同体的新背景下,我国新兴产业对锑、稀土、钨、石墨等战略性矿产原材料的需求越来越大,也越来越重视以上矿物资源的分选技术研究[1].浮选法作为应用最广泛的一种选矿方法,通过在矿浆中添加化学药剂来达到有用矿物和脉石矿物分离的目的[2-3].目前国内大部分选矿厂还是主要依赖操作工人根据经验对药剂量进行调整.这种以人工添加方法带来的弊端就是工况波动频繁,难以使浮选过程处于最佳运行状态,易导致药剂量消耗大、人工劳动强度大、矿物回收率低、企业经济效益低.因此,开展先进的浮选过程药剂量优化控制方法的研究对于减少资源浪费、减轻工人劳动强度、提高生产效率显得尤为重要.

近年来,国内外学者对浮选过程药剂量控制做了不少研究,并取得了一定成效.如基于模型的浮选过程药剂量控制方法[4-6],基于神经网络的药剂量控制方法[7-8],基于专家系统的药剂量控制方法[9-10]和基于计算机视觉的药剂量控制方法[11-14].尽管以上浮选过程药剂量控制方法在一些情况下是有效的,但是在实际应用中,存在以下问题有待进一步研究:1)对于具有动态不确定性的浮选过程,内部机理复杂、缺乏准确的在线测量工具,对浮选过程动态模型的识别具有一定难度,且以上基于模型的控制方法均未考虑外界扰动对系统的影响;2)基于人工神经网络的药剂量控制方法需要大量的可调参数(网络权值).当训练样本较多时,会出现计算量大和过拟合的情况,当可用于训练的数据数量减少(自由度减少)时,泛化能力就会丧失,理论和学习算法还有待于进一步完善和提高;3)基于模糊或基于规则的专家系统控制方法存在当知识集不完备,或对于未考虑到的情形,系统容易陷入困境,且对诊断结果的解释能力弱等缺点,同时又存在人工干预多、推理速度慢、精度较低等缺点,很难实现自适应学习的功能.尤其是随着时间的变化,基于专家系统的控制方法会使控制行为饱和,如何应对计算复杂度也是一个棘手的问题;4)基于计算机视觉的药剂量控制方法对人工特征提取算法的依赖度高,且在特征提取过程中易受噪声或外界光源扰动影响,容易出现收敛性和稳定性问题.

随着信息科学技术的发展和工厂自动化程度的提高,蕴含工业过程运行信息的数据被实时获取和存储,现代工业已经迎来了数据驱动时代的曙光.基于数据的控制方法在化工、高分子材料、钢铁、制药、配电网等工业生产过程中有着广泛的应用.与传统优化控制方法不同的是,自适应动态规划(adaptive dynamic pro-gramming,ADP)技术是最优控制领域新近兴起的一种基于数据的近似最优方法,是当前国际最优化领域的研究热点[15-21].近年来,ADP算法在理论研究和实际应用中已取得丰硕的成果,且展现出巨大的发展潜力,其应用范围深入到工业生产过程、电力系统、航空航天和自动驾驶汽车等各个领域[22-27].然而在有色冶金领域,特别是ADP技术在浮选过程中的应用却鲜有涉及.

因此,本文针对浮选过程的动态不确定性,传统基于模型/专家系统/神经网络/计算机视觉的药剂量控制方法在模型获取难、知识集不完备、解释能力弱、稳定性差等方面的问题,从浮选过程中大量在线和离线运行数据出发,深入发掘数据中隐含的系统信息,基于现代控制理论、前馈控制原理、强化学习和自适应动态规划技术,研究和设计数据驱动的浮选过程加药量自适应优化控制方法,以提高矿产资源利用率、减轻对操作人员人工调整药剂量的依赖性具有重要现实意义.

本文的研究框架如下:第2节对浮选槽工作机理进行描述,并建立锑浮选过程机理模型,为验证后续数据驱动的药剂量优化控制方法奠定基础;第3节给出浮选过程药剂量优化控制问题;第4部分详细介绍一种基于值迭代的药剂量自适应最优控制算法,并对所提出算法的收敛性和闭环系统的稳定性进行严格分析;第5部分给出仿真结果和已有方法的对比,以说明数据驱动控制方法的优越性;最后是本文结论和未来工作安排.

2 锑浮选过程单槽双相机理建模

针对传统针对浮选槽机理模型的研究,大都是建立在假设浮选槽内矿物颗粒与气泡均匀混合的理想情况下,本文根据矿物颗粒-气泡在浮选槽内的分布不均匀性,将浮选槽分为泡沫相和矿浆相进行研究,并在两相结构基础上,根据物料守恒原理和两相之间的物料传输特性,建立浮选槽双相机理模型,为后续的药剂量优化控制研究工作奠定基础.

2.1 浮选槽工作机理

浮选槽的工作机理如图1所示.浮选槽内配有一个叶轮和输气管,用于搅拌矿浆和向矿浆内充气.浮选药剂和矿物原料被添加到浮选槽,疏水性矿物随着叶轮的搅拌与气泡发生碰撞并附着在气泡表面上,向上移动形成泡沫层,经刮板从浮选槽中刮出,成为精矿产品.与此同时,亲水性矿物滞留在矿浆中,从浮选槽底部流出,形成尾矿产品.浮选过程的实质是利用矿物颗粒表面的疏水性和亲水性来收集目标矿物颗粒,使有用矿物的回收率最大化.为达到理想的浮选性能,可通过浮选药剂选择性地改变矿物颗粒表面的物理化学性质,以达到有用矿物和脉石矿物分离的目的.因此,可以通过调节药剂的添加量来控制浮选性能.

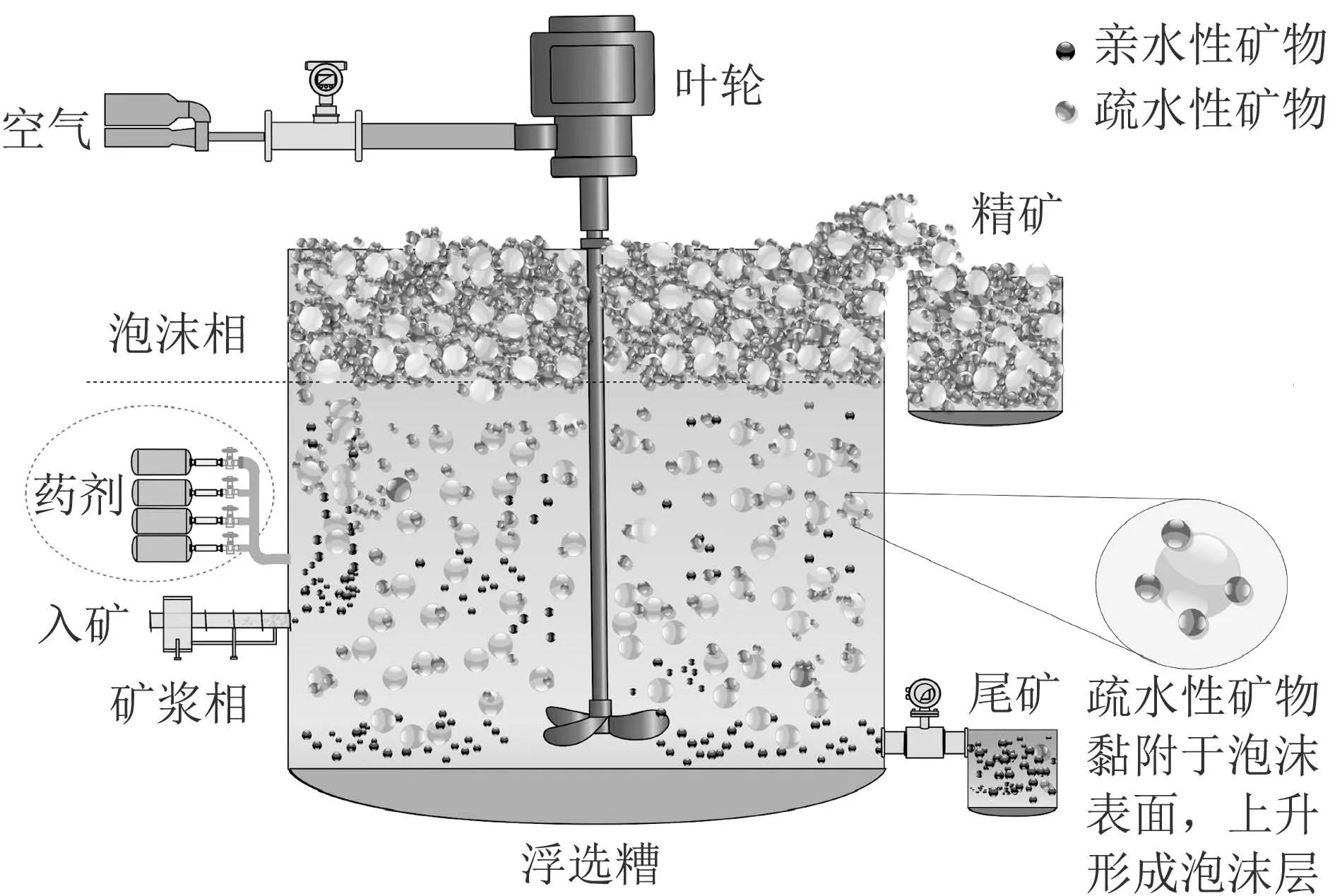
图1 浮选槽结构图Fig.1 Structure of a flotation tank

由于浮选过程的复杂性和动态不确定性,建立严格且精确的数学模型有一定的困难.但是,工业生产过程中存在大量数据,这些生产数据在一定程度上可以反映过程机理,对浮选过程建模具有很好的参考价值.可以看出,泡沫相和矿浆相颗粒-气泡之间的微观结构使浮选动力学模型的建立变得复杂.鉴于以往的单相模型都是把浮选槽内的物料看作一个整体,忽略了其中泡沫相与矿浆相之间的差异.本文从浮选过程机理出发(至少在定性意义上),在保持浮选过程模型结构足够简单的同时,用现场数据对其进行验证.首先,在文献[28]的基础上,对矿物颗粒与气泡在浮选槽内部存在的4种状态进行分析,并根据质量平衡模型,建立矿物颗粒-气泡在浮选槽内每种状态下的动态关系式,结构如图2所示.

图2 浮选槽内矿物颗粒的4种状态Fig.2 Four states of mineral particles in a flotation tank

其中:ψLP表示矿浆相的矿浆中单位体积内有用矿物颗粒的个数,VLP为矿浆相中矿浆体积(m3),kPAT为矿浆相中矿物颗粒与气泡的附着速率常数,kPDT为矿浆相中矿物颗粒与气泡的分离速率常数,QFeed为入矿流速(ml/min),QT为矿物颗粒向底流槽的传输速度(ml/min),QR为矿物颗粒从泡沫相向矿浆相的回落流速(ml/min),kR是矿物颗粒从泡沫相向矿浆相的回落速率常数,QE为夹带矿物颗粒从矿浆相向泡沫相的流速(ml/min),ψBP表示矿浆相的气体中单位体积内有用矿物颗粒的个数,VBP为矿浆相中气体体积(m3),QA为空气流速(m3/(槽·min)),QAT为从矿浆相到尾矿底流槽的空气流速(m3/(槽·min)),ψLF表示泡沫相的矿浆中单位体积内有用矿物颗粒的个数,VLF为泡沫相中矿浆体积(m3),kFAT为泡沫相中矿物颗粒与气泡的附着速率常数,kFDT为泡沫相中矿物颗粒与气泡的分离速率常数,ψBF表示泡沫相的气体中单位体积内有用矿物颗粒的个数,VBF为泡沫相中气体体积(m3),QC为矿物颗粒向溢流槽的传输速度(ml/min),QAC为从泡沫相到溢流槽的空气流速(m3/(槽·min)),V为浮选槽体积(m3),VTF为泡沫相体积(m3),VTP为矿浆相体积(m3).

然后,将方程(1)-(4)中泡沫相和矿浆相的矿物颗粒(自由、附着在气泡上的颗粒)分别相加,可以得到

假设矿浆相和泡沫相中附着在气泡上的矿物颗粒与自由颗粒之间存在某种物理平衡:

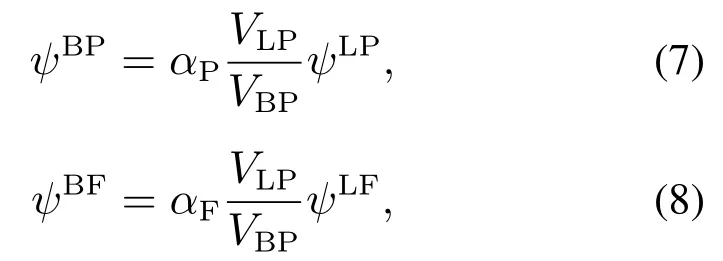
式中αP和αF分别为矿浆相中矿物颗粒与气泡的附着分离速率常数以及泡沫相中矿物颗粒与气泡的附着分离速率常数.式(7)和(8)可写为

因此,矿浆相中每单位体积的粒子数可表示为

将式(7)代入,可得

同样地,泡沫相中每单位体积的粒子数可以表示为

将式(7)-(8)(12)-(13)代入到式(5)-(6)中,可得

为简化模型,做出以下假设:

假设1矿浆相的矿物颗粒与气泡完全混合;

假设2泡沫相的矿物颗粒与气泡完全混合;

假设3矿物颗粒的大小和形状均匀;

假设4在稳态条件下,QA=QAC+QAT;

假设5QC/QAC=VLF/VBF,QT/QAT=VLP/VBP.

基于泡沫相和矿浆相分别完全混合的假设,可建立一组矿浆相与泡沫相的液态和气态物料平衡方程对浮选动态过程进行描述,式(14)-(15)可写成

式(16)-(17)分别表示矿浆相和泡沫相中的矿物质量平衡,式(18)和式(19)分别表示矿浆相和泡沫相的液态平衡,其中:

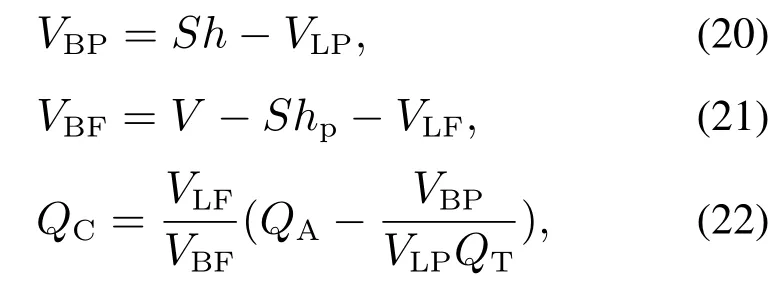
式中:S为浮选槽面积,h为浮选槽高度,hp为液位高度.

为建立加药量与浮选指标之间的关系模型,定义尾矿品位R1和精矿品位R2:

将式(23)与式(24)代入式(16)和式(17)中,可转化为与尾矿品位、精矿品位有关的表达式:

为从最优控制问题分析入手,对模型进行了修正,以研究操作变量对浮选性能的影响.根据文献[29]可知

其中:δ是气泡周围的薄膜厚度,dBP是矿浆相平均气泡直径,µF为泡沫相平均含气量,r1和r2是随工况变化的变量.

式(25)与式(26)仍然保留了模型(1)-(4)的基本特征,区分了矿物颗粒-气泡在矿浆相和气泡相的附着/分离机理以及两相之间的传输机理.由于在浮选现场,空气流速QA、矿物颗粒向底流槽的传输速度QT和向溢流槽的传输速度QC通常首先调整到一个合理的值,并在生产期间保持不变.因此,模型中未知量是泡沫相中矿物颗粒与气泡的附着分离速率常数αF、矿浆相中矿物颗粒与气泡的附着分离速率常数αP及泡沫相向矿浆相的回落速率常数kR,这3个参数均受浮选药剂(PH 值、捕收剂、活化剂和起泡剂)影响.

2.2 加药量与浮选指标动态模型建立

从经验来看,PH值O1通过在矿浆相改变矿物表面性质,从而影响矿物的可浮性.在文献[30]和[31]的基础上,可知矿浆相中矿物颗粒-气泡的附着分离常数αP与O1成比例关系.此外,αP还受捕收剂O2的影响,因为捕收剂可以促进有用矿物呈现出疏水特性,从而有利于矿物颗粒与气泡之间的附着.随着O2的增加,αP也在一定范围内增长[32].所以,可假设

而泡沫相中的矿物颗粒-气泡的附着分离常数αF以及矿物颗粒从泡沫相向矿浆相的回落速率常数kR主要受泡沫停留时间的影响,泡沫停留时间与活化剂O3和起泡剂O4有关.因为随着活化剂和起泡剂的增加,气泡粘度增加,气泡在矿浆相的停留时间增长.因此,有用矿物回落将会变得困难,从而影响最终的精矿品位和尾矿品位[33-34].可假设αF和kR与O3,O4之间的关系为

式中:R1和R2分别表示尾矿品位和精矿品位,m1,m2,m3,m4,m5以及r1,r2为待辨识参数.

综上,加药量是通过影响矿浆相的附着分离速率常数、泡沫相的附着分离速率常数以及泡沫相向矿浆相的回落速率常数对最终的精矿品位和尾矿品位产生影响.根据生产数据分析,空气流速QA以及矿浆液位hp会在一定范围内较小的波动,但其平均值基本稳定在一定的数值.所以,可将矿浆相体积以及泡沫相体积看作是常数.PH值O1、捕收剂流量O2(ml/min)、活化剂流量O3(ml/min)和起泡剂流量O4(ml/min)作为动态模型的控制量,通过对药剂量进行优化调整,对矿浆相和泡沫相的颗粒-气泡运动行为产生影响,以提高有用矿物回收率.

3 浮选过程加药量控制问题描述

为简化控制器的设计任务,将浮选过程的非线性动态模型在稳定运行状态下近似线性化,即将式(35)和式(36)在平衡点(R1eq,R2eq,O1eq,O2eq,O3eq,O4eq)附近进行线性化处理.令

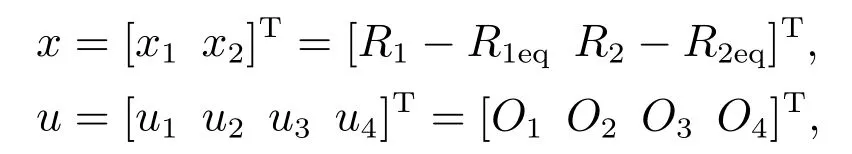
则系统(35)和(36)在平衡点附近的线性化状态方程为

式中:x表示要跟踪的系统状态向量,u表示控制输入向量,Ac与Bc为系数矩阵,Dc表示外界扰动,具体参数见文献[35].根据输入信号在每个采样时刻的运动轨迹,采用零阶保持器方法可将连续时间系统(37)离散化为[36]

h是采样周期.因式(38)可控性矩阵和可观性矩阵均满秩,可知该线性离散系统是可控和可观的.

本文的主要目标是设计一个控制器

使得跟踪误差xk随时间k趋于无穷而趋于零.其中:K ∈R4×2是反馈增益矩阵,U ∈R是前馈增益矩阵.

定理1如果Ad-BdK的所有特征值都严格位于单位圆内,则

式(40)为线性调节器方程(linear regulation equation,LRE).基于最优控制理论和前馈控制原理[37],可将浮选过程的药剂量控制问题转化为两级优化问题(问题1和问题2):通过求解问题1可知式(40)的最优前馈分量U∗,求解问题2得出最优反馈增益K∗,从而得到最优控制器=-K∗xk+U∗,以实现抑制外部干扰和跟踪误差为零的控制目标,即:=0[38].

问题1

问题2

对于初始状态x0∈Rn,其中:Q=QT≥0,R=RT>0.根据线性最优控制理论,对于离散时间系统(38),最优反馈增益K∗可由P∗计算得到.其中P∗=P∗T>0 是以下离散时间代数Riccati 方程(discretetime algebraic riccati equation,DARE)的唯一解:

因此,可知最优反馈增益K∗

但是P在DARE(42)中是非线性的,很难直接求解.在常规基于模型的控制器设计方法中,通常采用文献[39]提出的值迭代(VI)算法寻找式(42)-(43)中的近似解P∗-K∗,方程如下:

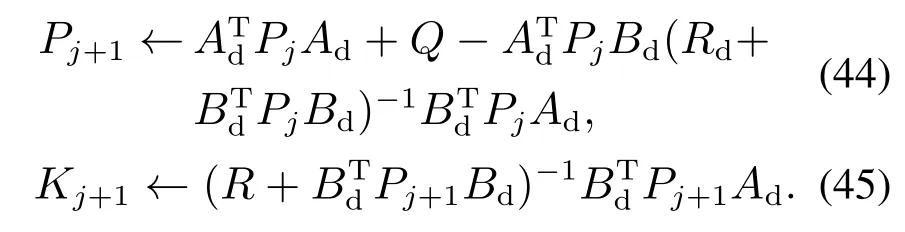
由式(44)-(45)可以看出,上述基于模型的方法建立在状态模型的参数Ad,Bd和Dd已知的情况下.然而,在实际的浮选过程中,输入和状态数据的实时变化,浮选过程的动态不确定性、内部参数间互相耦合互相影响,建立精确的数学模型是一件非常复杂的工作.

鉴于此,接下来将提出数据驱动的方法解决浮选过程中药剂量的最优控制问题,控制目标是设计一个ADP控制器和自适应控制策略,以保证在药剂量消耗最少的情况下,系统状态xk能够跟踪给定值,且跟踪误差较小,具体控制结构如图3所示.在线X-Ray荧光分析仪提供元素浓度,实时计算精矿品位R1和尾矿品位R2,根据测量值R=[R1R2]T与参考状态Req=[R1,eqR2,eq]T之间的误差,采用基于VI 的ADP 算法计算反馈控制增益K.同时,在ADP控制器中加入一个前馈补偿器U用于抑制干扰,以此实现浮选过程药剂量的优化控制.

图3 基于ADP控制器的浮选过程药剂量优化控制框图Fig.3 The reagents optimal control diagram in flotation process based on ADP controller

4 数据驱动的药剂量优化控制方法

为设计数据驱动的加药量自适应迭代学习控制方法,将系统(38)写为

基于以上定义,将给出基于VI的ADP控制器设计方法,在VI迭代算法中,是从一个随机值函数开始,然后在迭代过程中找到一个新的(改进的)值函数,直到得到最优值函数.通过式(44)和式(46),值迭代方程可以写为

5 仿真结果

为验证所提出数据驱动控制方法的有效性和稳定性,收集了浮选厂4000组药剂量添加数据,以及相应的4000组精矿品位和尾矿品位数据对浮选过程药剂量控制问题进行建模.采用龙格-库塔-费尔博格法和1stOpt 提出的通用全局优化算法,最小化如下的目标函数:

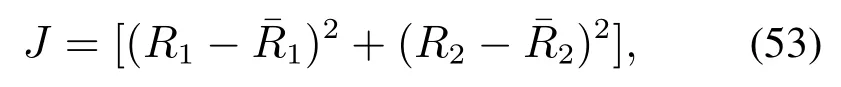
对第2节建立的动态模型(35)-(36)中的未知参数m1,m2,m3,m4,m5以 及r1,r2进 行 辨 识.式 中R1和R2分别表示实际采样点现场收集到的尾矿品位和精矿品位,可通过X 荧光分析仪在线检测得到,和表示在每个采样点上尾矿品位和精矿品位的模型计算值.系统模型(38)可写为

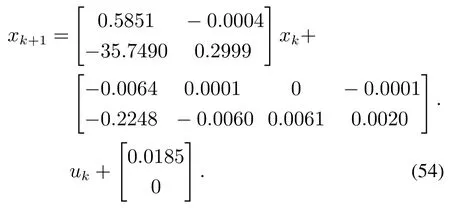
权重矩阵设为Q=,R是单位矩阵,采样周期为1 s.为验证所提出数据驱动方法的有效性,通过状态空间模型(54)的矩阵系数Ad,Bd,Dd求解DARE(42)计算最优控制增益H∗和K∗.

5.1 ADP控制器下仿真结果

在式(54)基础上,建立仿真环境,仿真中添加的噪声e=是由随机发生器产生.其中,wi为[0,100]里的随机数,i=1,2.

根据浮选生产过程中采集的状态和输入数据,使用基于VI的ADP算法迭代学习最优控制器的反馈增益Kj.从图4可以看出,11次迭代后,使用基于VI的ADP算法迭代学习到的Hj和Kj已经收敛到经模型系数矩阵计算得到的最优值H∗和K∗,从而可得自适应最优控制器uk=-Kxk+U.

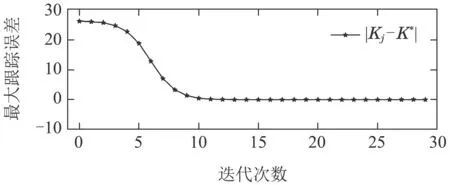
图4 Hj和Kj及其最优值比较Fig.4 CompareHj andKj with optimal values

在k=30时,将本文提出的基于VI的ADP算法迭代学习到的最优控制策略应用于闭环系统中,得到以下结果:尾矿品位R1和精矿品位R2的跟踪误差x1与x2以极小的跟踪误差收敛到0,如图5 所示.同时,图6给出了ADP控制器所建议的药剂添加量u=[u1u2u3u4].

图5 基于ADP控制器的系统状态Fig.5 System states under ADP controller

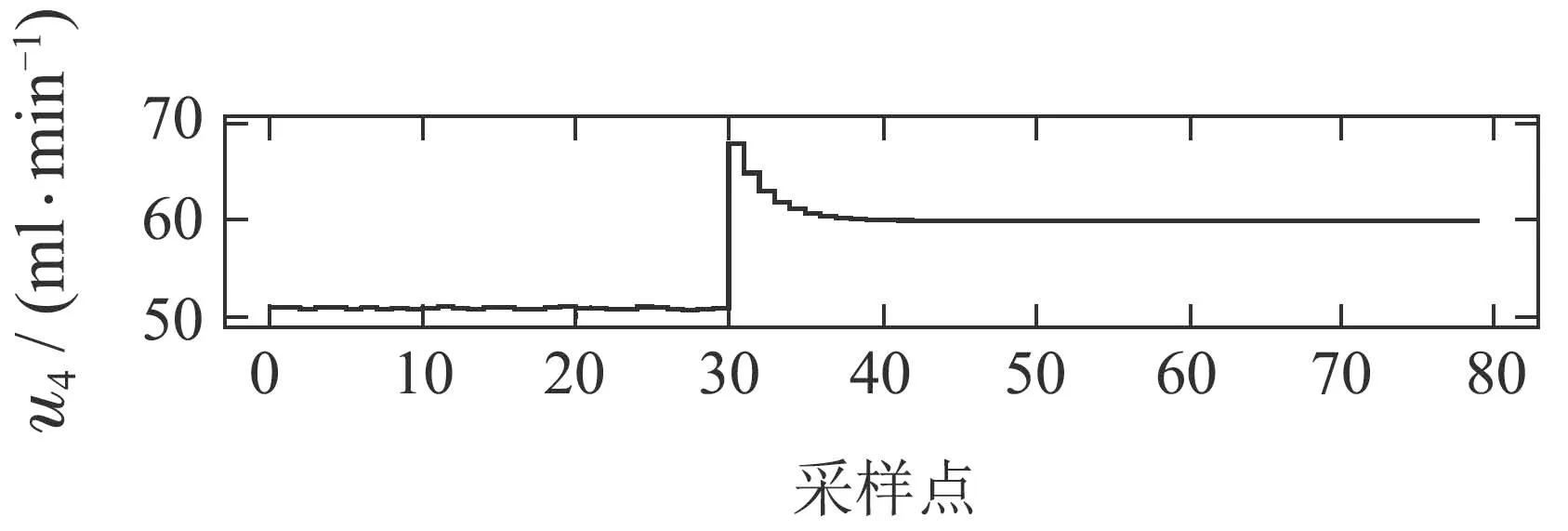
图6 基于ADP控制器的控制输入Fig.6 Control inputs under ADP controller

5.2 MPC控制器下仿真结果

为评估所提出基于VI的ADP算法的有效性,应用模型预测控制(model predictive control,MPC)方法,与数据驱动的ADP控制方法进行了比较.目标函数定义为

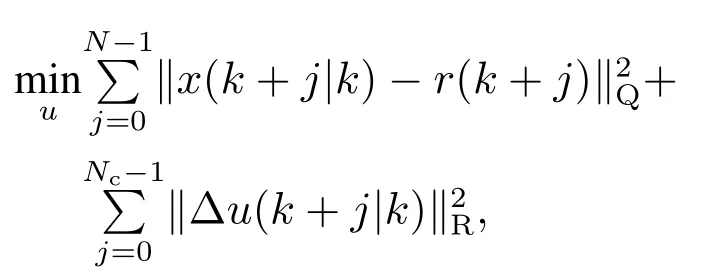
其中:r(k+j)=0为跟踪误差xk的目标值,uk为药剂消耗量.MPC 控制策略采用二次规划(quadratic programming,QP)结构来求解[40],预测时域N和控制时域Nc分别设为20和2.图7和图8分别给出了基于MPC控制方法的系统状态跟踪误差和控制输入.

图7 基于MPC控制器的系统状态Fig.7 System states under MPC controller

图8 基于MPC控制器的控制输入Fig.8 Control inputs under MPC controller

从图8仿真结果可知,MPC控制器下浮选药剂u1,u2,u3和u4比ADP控制器下所建议的药剂量消耗分别高了4.9%,11.3%,0.8%和6.8%,药剂量消耗高会增加选矿成本,不利于浮选厂的经济效益.此外,从图7可以看出,尾矿品位的跟踪误差x1不能完全按照期望的轨迹运行,使得控制精度难以满足生产要求.

5.3 两种控制器性能比较

表1分别给出了ADP和MPC两种控制器下,系统状态收敛性能和控制输入.通过结果对比可以看出,本文提出的数据驱动的ADP控制方法,系统状态的跟踪误差较小、药剂消耗量较小,并且能很好地解决基于MPC控制方法依赖模型的缺点.由此可知,基于VI的ADP算法在不了解浮选过程数学模型的情况下,仅依靠输入和测量状态数据即可对浮选过程药剂量进行优化控制,且能够有效抑制外界扰动.

为进一步说明本方法的有效性,对锑浮选现场的人工加药量调节情况进行记录.该锑浮选厂采用三班倒8小时工作制,图9-12分别为2019年4月186条人工对PH值、捕收剂流量、活化剂流量和起泡剂流量的调节情况.其中:PH值的波动范围在6.1～7.96之间,捕收剂流量的波动范围在204.46～471.26 ml/min之间,活化剂流量的波动范围在510.83～696.8 ml/min之间,起泡剂流量的波动范围在44.13～129.64 ml/min之间.

综上,本文提出数据驱动的ADP控制方法利用生产数据信息进行仿真验证的结果,与实际浮选过程真实药剂量调节具有较好的一致性,可解决实际浮选现场采用人工调节方式药剂量波动大,易导致生产过程不稳定的问题.

表1 ADP控制器与MPC控制器性能比较Table 1 The performance comparison between ADP controller and MPC controller

图9 人工调节PH值Fig.9 Manually adjustment of PH value

图10 人工调节捕收剂流量Fig.10 Manually adjustment of collector flow rate

图11 人工调节活化剂流量Fig.11 Manually adjustment of activator flow rate

图12 人工调节起泡剂流量Fig.12 Manually adjustment of frother flow rate

6 总结

考虑到浮选过程的动态不确定性和外界扰动,本文采用基于VI的ADP控制方法,解决了浮选过程加药量优化控制问题.通过将浮选药剂控制问题转化为两级优化问题,以最小化跟踪误差和药剂消耗量组成的二次型代价函数为目标,借助数据驱动的自适应动态规划方法,利用值迭代算法设计一种基于学习的自适应最优控制策略.同时,引入前馈补偿分量以抑制外界扰动.与传统的控制器设计不同,基于VI的ADP控制算法可以在不需要知道浮选过程模型和初始控制策略的情况下,仅通过实时采集浮选过程生产数据便可自适应的学习最优控制策略,从而跟踪期望的精矿品位和尾矿品位.这种数据驱动的自适应迭代学习控制方法具有较强的抗干扰能力,保证了浮选过程的稳定性.

随着分布式控制策略的集成,数据驱动的控制方法不仅可用于控制整个浮选厂的矿浆液位、通风量等其它控制变量,也可用于磨矿分级过程控制,今后将以不同控制器之间的协调优化控制为目标,为选矿过程全流程自动控制提供部分关键技术.