长江口航道黏性原状土冲刷特性试验

黄健钧，陈国平，马洪蛟

(1.河海大学 港口海岸与近海工程学院，江苏 南京 210098；2.河海大学 海岸灾害及防护教育部重点实验室，江苏 南京 210098)

近年来，随着我国海洋经济和水运经济的不断开发，越来越多的工程在施工过程中遇到与细颗粒泥沙起动特性有关的问题。以往对泥沙基本运动规律进行研究时，一般采用普通明渠水槽和环形水槽[1-2]来做室内物理模型试验。然而对于细颗粒泥沙往往带有黏性，临界起动的水动力条件很强，普通明渠水槽和环形水槽中无法达到试验所需的起动流速和起动切应力，学者们提出了采用有压矩形管试验对原状泥沙的冲刷特性进行分析。目前来说，学者们普遍认为泥沙的冲刷性质取决于泥沙自身的条件及水流动力条件。2005年，洪大林等[3]总结了国内外学者在泥沙起动研究和黏性土的起动模式、影响因素等方面的研究成果，提出影响黏性土起动的因素主要有土的物理因素、土力学参数、化学特性等，并且认为今后的研究重点应放在黏性原状土上，在此基础上再进行重塑土试验。2006年，时连强等[4]以黄河三角洲的沉积物为例，通过测定沉积物的结构、颗粒组成、密度和含水率，进行了分层沉积物的冲刷试验，发现沉积物临界起动切应力与含水率、中值粒径成一定的负相关关系，与黏土含量呈显著正相关关系。2011年，孙志林等[5]对钱塘江河口河床获取的28个岩芯进行起动和冲刷水槽试验，根据冲刷试验结果确定了冲刷率公式的指数和冲刷常数，发现未充分固结的淤泥冲刷率与相对剩余切应力的二次方成正比，而固结已久的淤泥冲刷率与相对剩余切应力呈线性关系。2013年，雷文韬等[6]为研究黏性泥沙的冲刷规律，引入床沙相对干密度以反映冲刷源项与床沙干密度的关系，提出分别适用于弱固结和强固结河床的冲刷源项公式，并采用室内黏性泥沙的冲刷试验资料确定公式中各系数。2016年，吴月勇等[7]通过物理模型试验，对福建晋江围海工程的6组粉沙、8组细沙、7组中粗沙原状土样进行冲刷率试验，考虑中值粒径对冲刷率表达式的影响，分别得出了粉沙、细沙、中粗沙的冲刷率表达式中的能量指数和冲刷系数。

自长江口12.5 m深水航道工程开辟以来[8]，关于航道泥沙回淤的问题已经开展了大量的研究[9-11]，但是关于长江口航道底床回淤原状土的冲刷特性却鲜有研究。因此，本文对长江口航道的底质淤泥质粉沙原状土样进行封闭有压矩形管槽的冲刷物理模型试验，分析淤泥质粉沙原状土的起动特性和冲刷特性，以及随土样深度的变化趋势，给长江口航道工程提供相关的科学依据。

1 物理模型试验

1.1 试验装置与土样

由于黏性原状土的土颗粒之间黏结力较大，导致泥沙的起动流速也较大，一般的水槽装置难以产生足以让黏性土起动以及冲刷的水流流速。因此，本次试验采用封闭有压的有机玻璃水槽来研究长江口航道黏性原状土的冲刷特性。该水槽系统一般包括矩形有机玻璃水槽、测量管、土样桶和上下游的聚氯乙烯(PVC)管，如图1所示。其中矩形有机玻璃水槽长200 cm，土体试样放置在圆形土样筒内如图2所示，在土样筒的上下游各布置1个测压管，测压管间距设置为130 cm。土样筒与升降装置连接，通过控制电压调节升降装置的上下移动速度，该水槽的最大流量可达30 Ls，此时产生的最大流速为6.67 ms。在本次试验中，通过直读式电磁流量计直接读出水槽里面的瞬时流量，从而得出瞬时水流流速。

图1 封闭有压的有机玻璃水槽

图2 土样筒里的黏性原状土试样

在本次试验中，原状土取自长江口航道南港水域，取样时间为2019年5月。原状土样采样严格按JTS 133—2013《水运工程岩土勘察规范》要求执行，通过分层采样，同时保证土样没有过大扰动，使原状土样满足试验的需求。本文分别对S1、S2和S3钻孔共21个土样进行冲刷试验，每个土样都含有不同含量的黏性颗粒(粒径小于0.005 mm的颗粒)，每个试样的取样深度和中值粒径见表1。

表1 原状土取样深度和中值粒径

1.2 试验方法

根据以往的研究，将“芯样表面出现许多小的局部破坏或撕裂并伴随少量冲刷发生”定义为泥沙的“临界起动”，如图3所示。试验开始时，将原状土缓慢装进土样筒，并且确保土样没有过大的扰动，通过控制电压使升降装置上升，从而带动土样筒上升至与水槽齐平。接着，逐步加大矩形水槽里面的水流流量，一边调节流量，一边仔细观察原状土试样表面的泥沙起动状况。当原状土试样出现如图3所示的现象时，维持水槽流量不变，记录瞬时水槽水流流速为泥沙起动流速。然后，继续加大水槽流量的同时，控制升降装置从而调节原状土试样上升速率，当土样在该时间段内高度变化较小且始终与水槽底部保持平齐，则说明冲刷速率和土样上升速率平衡，此时该土样上升速度即为冲刷速率。由于泥沙起动和冲刷的判断较为主观，因此试验中随机性和误差相对较大，为保证试验的准确性，需要重复进行起动和冲刷试验，当相临3次试验结果误差在5%以内时，取3次试验数据的平均值作为最后的试验结果。

图3 土样临界起动状态

1.3 起动切应力与冲刷率计算公式

为了能够定量研究黏性原状土的冲刷特性，需要对土样起动切应力和冲刷率进行计算，计算方法如下：

1)床面切应力与摩阻流速的关系为：

(1)

(2)

式中：τ为床面切应力(Nm2)；v*为摩阻流速(ms)；ρ为水的密度，为1 tm3；p1-p2为上下游测压管压力差；R为水力半径(m)；Δz为上下游测压管水头差(m)；l为两测压管间距(m)；J为水力坡度。

2)根据土样冲刷高度Δh(mm)及冲刷历时Δt(s)，测得的冲刷率与单位时间冲刷高度关系为：

(3)

式中：qw为原状土冲刷率(kg·m-2·s-1)；ρ1为沉积密度(tm3)。

3)原状土的冲刷系数，其表达式为：

(4)

式中：M为冲刷系数，是土壤抗冲性的一个重要指标；qw为冲刷率；τb为床面切应力(Nm2)；τc为床面临界起动切应力(Nm2)。

2 试验结果与分析

通过封闭有压矩形管槽冲刷试验，根据每个原状土样本的试验结果(表2)，分别从土样密度、临界起动切应力、冲刷率和冲刷系数的角度对试验结果进行讨论。

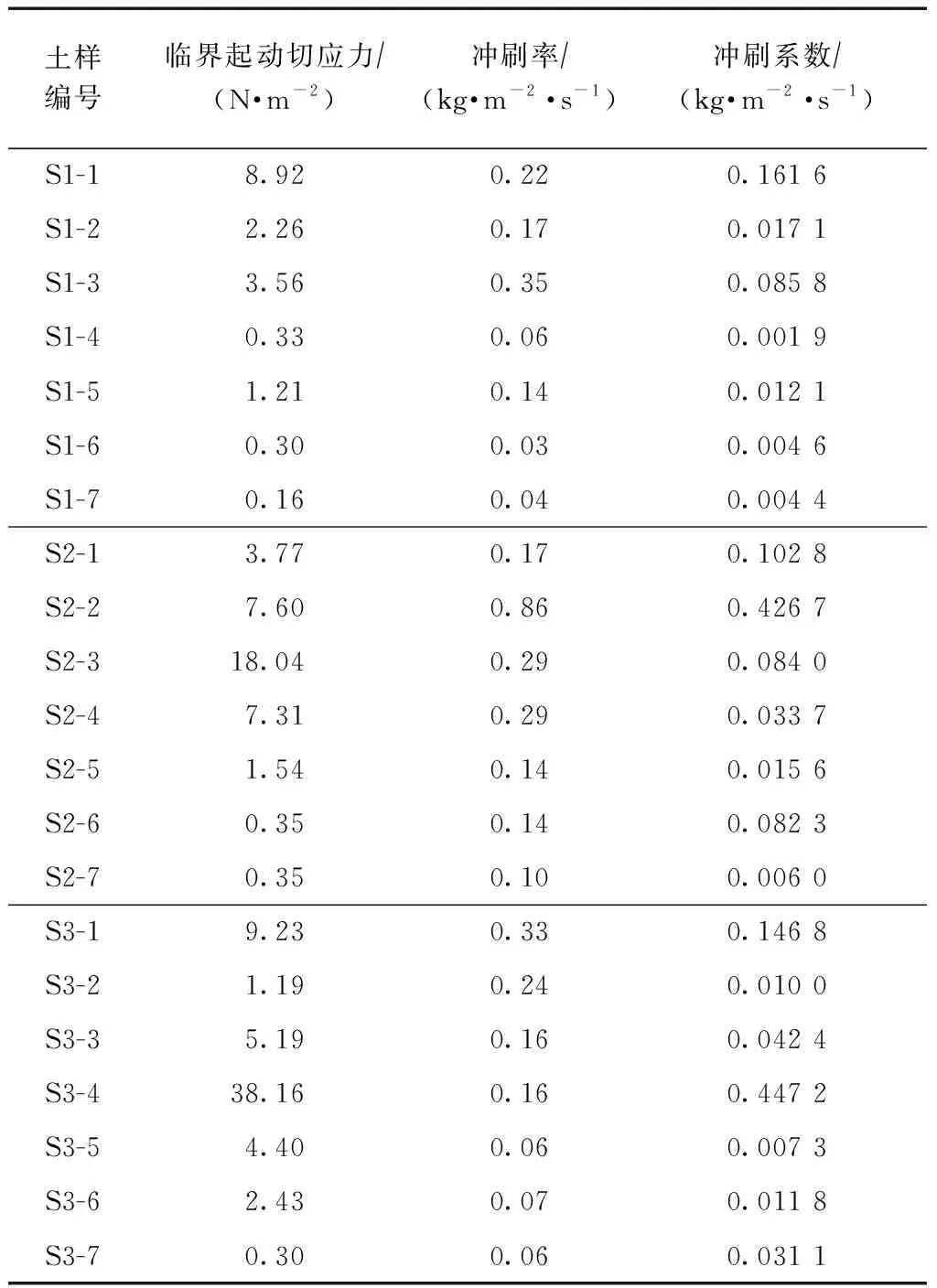
表2 原状土试验结果

2.1 土样冲刷前后沉积密度

试验原状土样冲刷前和冲刷后的沉积密度见图4。可以看出，取样于长江口航道上海崇明段的底质泥沙的沉积密度在1.6～2.0 tm3，低于常见的矿质土壤密度2.7 tm3，属于一般性黏土的范围。此外土样沉积密度在冲刷前后的变化程度不大，冲刷后的密度略小于冲刷前的密度。这是由于本次试验的土样大多数属于淤泥质粉沙土，有一定的含沙量并夹杂着部分淤泥。在水流的冲刷下，由于沙土没有黏聚力被最先冲刷剥离，而淤泥质土具有黏聚力不易被水流冲刷侵蚀，因此导致冲刷后的土样含沙量会减小，宏观上表现出土样的沉积密度降低。

图4 土样冲刷前后的沉积密度

2.2 临界起动流速对临界起动切应力的影响

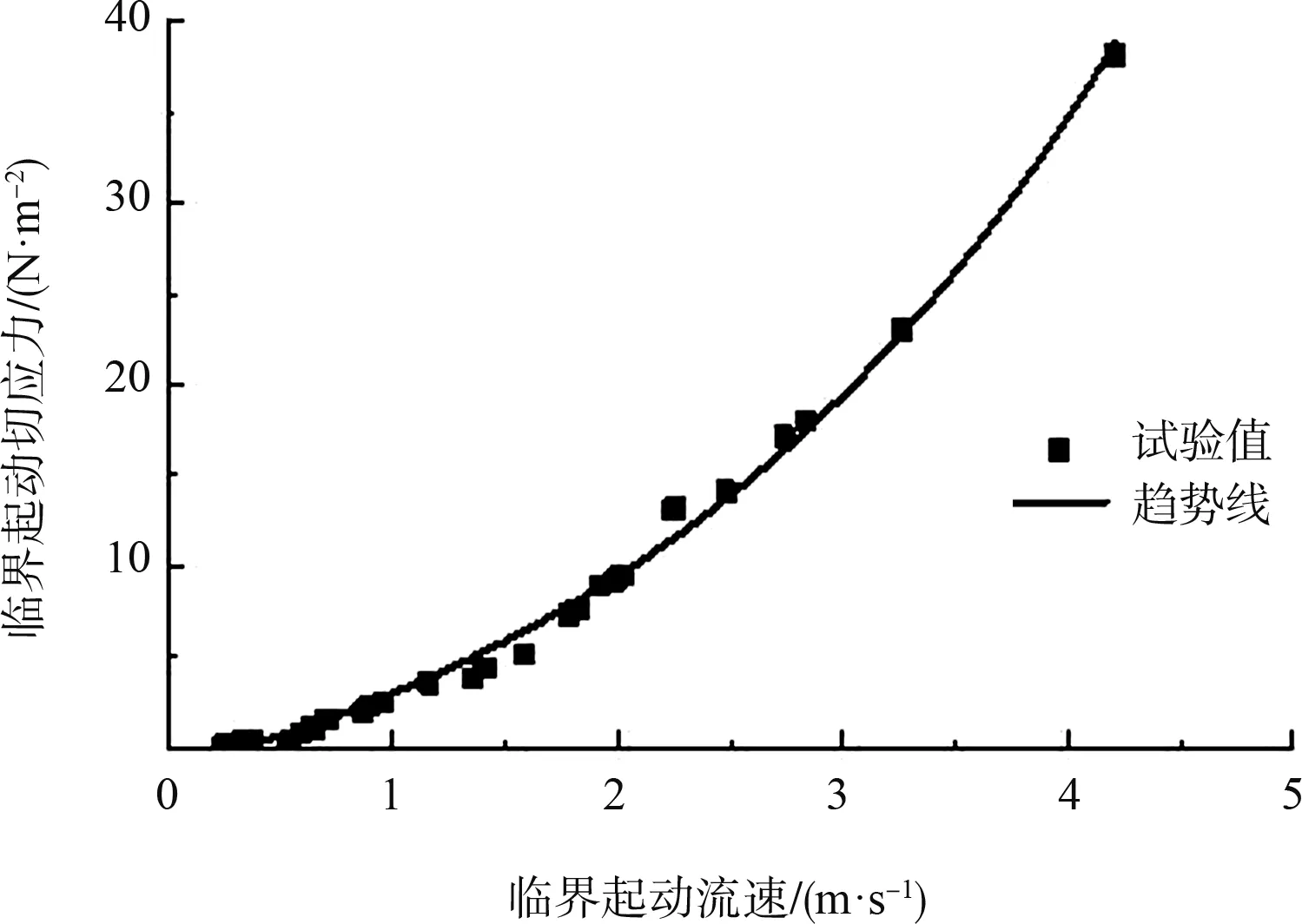
图5 临界起动切应力与临界起动流速关系

2.3 冲刷率随土样深度的变化

试验土样冲刷率随土样深度的变化情况见图6。可以看出，土样冲刷率在0.1～0.4 kg(m2·s)，随着土样深度的加大，冲刷率逐渐减小。这是由于天然土样在自然条件下会发生沉降固结，越往地底下的土层受到的固结应力越大。特别像位于长江口航道的底质淤泥黏土，在河床表面深度较浅的土层，受到水流的长期冲刷扰动作用，土的骨架结构较为疏松，因此容易受到水流侵蚀作用。而随着深度增大，土层的扰动较小，并且具有较高的固结应力，从而黏聚力和摩擦角均较大，导致其抗冲刷能力也较强，在相同条件下其冲刷率小于表层土样。

图6 不同土样深度对土样冲刷率的影响

2.4 冲刷系数随土样深度的变化

试验土样冲刷系数随土样深度的变化情况见图7。可以看出，试验土样冲刷系数在0～0.15 kg(m2·s)的范围内，随着土样深度的加大，冲刷系数逐渐减小，表现出2.3中冲刷率随土样深度的变化情况。一般来说土样的冲刷系数是土样本身特性的体现，能够保持在一个稳定的数值，不会随着外界的物理作用而变化。本次试验中随着深度的增加，土样的冲刷系数减小，表明位于长江口航道上海崇明段的底质泥沙随着深度分布不均匀，深度越大的泥沙抗冲刷能力越强，深度越浅的泥沙颗粒组成越不稳定，容易被扰动冲刷。

图7 不同土样深度对土样冲刷系数的影响

3 结论

1)本次试验的土样属于一般性黏土，有一定含沙量并夹杂着部分淤泥，冲刷前后的泥沙沉积密度相当，其中冲刷后的土样含沙量较小，沉积密度略小于冲刷前。

3)随着土样深度增加，土样的冲刷率和冲刷系数均减小，这表明位于长江口航道上海崇明段的底质泥沙随着深度分布不均匀，深度越大的泥沙抗冲刷能力越强，深度越浅的泥沙颗粒组成越不稳定，容易被扰动冲刷。