水力式升船机组合阀运行方式优化*

王 蛟，胡亚安，薛 淑，李学义，巩 炎

(1.重庆交通大学，重庆西南水运工程科学研究所，内河航道整治技术交通行业重点实验室，重庆西科水运工程咨询中心，重庆 400016；2. 南京水利科学研究院，通航建筑物建设技术交通行业重点实验室，水文水资源与水利工程科学国家重点实验室，江苏 南京 210029)

为防止阀门损坏导致升船机无法运行等极端事故的发生，水力式升船机控制阀门需要采用多线并行的基本形式来提高运行可靠度。同时，水力式升船机具有以下运行特性[1]：空中运行阶段，要求阀门供流量大，尽量提高升船机的运行效率；对接阶段，要求阀门控流精确，尽量提高对接精度。景洪工程基于以上要求，采用了“一主两辅”的组合阀布置形式(图1)，主阀居中，流量系数较强；两侧为辅阀，过流能力较弱。

图1 组合阀示意

景洪工程最初采用三岔管来实现三阀并流，但原型观测发现三岔管振动明显。后经模型试验研究发现，在三岔管汇合段会形成“螺旋流”(图2)，多股水流互冲掺混，流态极不稳定，导致管道强烈振动[2]。景洪工程技术改造利用突扩体来改善活塞阀后的不利流态，减弱水流对管壁的直接冲击。但不论采用三岔管还是突扩体，并列多阀都存在一个组合阀流量分配问题。多股射流向同一有限腔体内排放水体，在满足升船机运行特性的基础上，为了尽量降低多股水流对汇合管段的冲击影响，如何合理地运行组合阀并分配三阀流量是一个亟待解决的问题。

图2 发生于阀后叉管汇合处的“螺旋流”

景洪工程组合阀运行方式优化问题的实质是多孔紊动射流问题，由于多孔紊动射流问题涉及孔型、孔间距、流量比等诸多因素，研究关注重点一般为流场结构等全域特性，因此一般采用数值模拟方法进行研究。针对实际工程问题，采用标准k-ε模型一般可以取得较为理想的模拟成果。但由于ε方程未考虑各向异性，对流场的精细研究，例如回流、漩流及分离流等就很难取得理想的研究成果。因此，为了深入研究多孔紊动射流的特性，取得更为精确的成果，需要改进模型。相关数值计算基础理论方面，国外研究起步较早，成果较多。Lakehal[3-4]、Theodoridis等[5]基于标准k-ε模型，在近壁层湍流应力中引入各向异性假设，其计算结果与试验资料吻合度有所提高；Rodi等[6]将流场划分为主流区和近壁区，对不同区域采用不同的计算模型，简称“两层模型”，该方法也提高了模拟精度；Leschziner等[7]和Tsao等[8]利用三维模型对各种涡黏模型和大涡模拟进行了比较，成果表明大涡模拟可以提高模拟精度；Kheirkhah等[9]采用多种湍流模型对三维壁面射流进行模拟研究，成果表明realizablek-ε模型和RSMs模型的模拟精度最为合理。

国内对于多孔紊动射流的相关研究起步较晚，研究内容多服务于实际工程。戴光清[10]基于k-ε模型研究了水垫塘内多股射流的流场特性，涵盖了入射间距、水股厚度和冲击角度等；杨忠超等[11]采用VOF法，基于向家坝工程对多股多层水平淹没射流进行了三维数值模拟，分析该类出流方式的流场结构和消能特性；龙新平等[12]采用Realizablek-ε模型研究多孔射流泵内部的流场结构，并尝试利用涡动理论分析泵内流体的混合机理；王晓鹏等[13]采用RNGk-ε模型研究不同间距对消力池流态的影响规律；牛万芬[14]采用RNGk-ε模型对船闸输水系统三维多孔壁面射流的消能特性进行研究，揭示了单孔、并行双孔紊动射流的消能机理；高猛等[15]运用两相流混合模型对横流中垂直出流式多孔射流进行数值模拟，观察多孔射流的分叉和融合现象，定量分析了多孔射流的融合位置及其浓度的变化，可为扩散器的理论研究和设计提供可靠的依据；李一明等[16]利用 Realizablek-ε湍流模型研究平行多孔射流的流场特性，分析多孔射流的卷吸与合并作用。

综上可知，多孔紊动射流的相关研究主要涉及流场结构、速度场、紊动场的分布规律，考虑了孔径、孔间距、速度比等影响因素，并已取得丰富的研究成果。但多孔紊动射流问题较单孔射流复杂得多，很难得到普适性的理论成果。多孔紊动射流间的相关作用规律、流场结构的产生机理等还有待深入研究。本文依托景洪工程，建立三维受限空间多孔紊动射流模型，研究充水阀门段组合阀的运行优化问题，可供类似工程参考借鉴。

1 数学模型建立

1.1 湍流模型

考虑到模拟范围内紊动射流对突扩体边壁的冲击会形成明显的回流、涡旋，因此采用可以模拟平均流动中的旋涡流、分离流等复杂流动的RNGk-ε模型作为计算模型[17]。RNGk-ε模型是在标准k-ε模型的基础上，对ε方程进行了改进，增加了一项Rε。

k方程：

(1)

ε方程：

(2)

式中：ρ为流体密度；k为紊动能；u为速度；μeff为有效黏性系数；Gk为湍流动能；ε为耗散率；t为时间；C1、C2为常数；αk和αε为有效普朗特数。

(3)

1.2 三维模型及网格划分

数模计算范围是水力式升船机的充水阀门段，主要包括阀前整流段、组合阀、突扩体和汇合管共4部分。为了更准确地模拟突扩体内部的水力特性，阀前整流段和汇合管段均取为10倍管径长度，以便稳定进出口边界条件。组合阀考虑主辅阀的流阻差异，与阀门原型保持一致，中间主阀流量系数较大，两侧辅阀流量系数较小(流量系数≈3:1)，三阀通径相等，并列排布。三维模型具体尺寸为：阀前整流段半径×长为0.8 m×8 m，组合阀3台，阀门通径为1.6 m，突扩体的长×宽×高为5.7 m×10.2 m×3.2 m，汇合管段半径×长为1.2 m×12 m。图3为计算模型的主要组成部分和边界条件。

图3 计算模型及边界条件

计算区域大小约为28 m×10 m×3 m(长×宽×高)，为保证计算精度，同时提高效率，采用混合网格进行网格划分。对圆管及突扩体等结构较简单的部分采用结构网格划分，减少网格数量；对阀门等几何复杂的部分采用非结构网格划分，同时对流速较大区域进行网格加密，确保精度。网格划分过程中，尝试了多种网格尺度(表1)，网格有效性由阀门流量系数表征，最终通过对比计算精度及效率来确定使用尺度。验算结果表明模型整体使用0.1 m、局部加密采用0.05 m的网格尺度时的计算效率较佳，精度合适，基本模型的网格单元总数约150万个。模型网格及局部细节见图4。

表1 网格有效性验证

图4 模型网格划分

1.3 模型验证

模型验证通过与物模试验相同工况进行对比计算来完成。物理模型同样基于景洪充水阀门段，适当概化，突扩体采用有机玻璃制作，采用1:10的模型比尺。验证对比区域选取主阀后突扩体廊道顶沿程测点(1#～7#)，见图5。

耳内镜下不同给药频率曲安奈德益康唑乳膏治疗真菌性外耳道炎的疗效观察（张思思 林川耀 陆玲 张小莉 刘晶 钱晓云 佘万东）4∶253

图5 模型照片

验证结果见图6，横坐标为测点与阀门出口的距离(L)，纵坐标为压力水头(H)。模型试验结果表明：阀后突扩体—主阀顶测点压力水头的时均变化有沿程逐渐增大的趋势，但整体变幅不大，验证工况下变幅在1 m水头以内。相对而言，数模计算结果整体略微偏小，压力水头变幅在0.5 m水头以内，但分布规律相似。计算值整体均略小于试验值，但偏差不大，验证工况下最大偏差不超过5%。为保证突扩体段压力的稳定性，三维模型突扩体后汇合管采用了直管，而试验模型采用的是弯管。弯管对突扩体水体出流有一定的阻尼作用，将略微增大突扩体段压力，因此造成了三维模型计算值整体略微偏小。

图6 验证计算结果对比

2 计算成果分析

本研究的主要思路是：针对组合阀典型运行方式进行不同流量比的阀门段流场特性三维数值模拟计算，分析其速度场、压力场等流场水力特性，揭示其流场水力特征；再以典型轴线沿程最大流速(Uo)和阀门通径(a)为比尺，对各典型工况的流场典型剖面中轴线(图7)流速分布进行无量纲分析，计算流场均匀度，讨论组合阀典型运行方式与流场均匀度的关系，确定组合阀的合理运行方式。主要计算工况见表2。

图7 流场分析特征轴线

表2 组合阀运行方式研究方案

2.1 典型阀门段水力特性

2.1.1主阀单独运行

主阀单独运行时，主阀中轴线沿程水力特性参数无量纲分布见图8。突扩体段(X=0～3.5a)射流流速迅速增加，在X=1.0a附近达到最大流速，这是活塞阀环状出流的汇聚过程；压力先迅速降低，而后基本维持稳定；紊动能在突扩体内部均较小，在汇合管入口附近逐渐增大。汇合管段(X=3.5a～11a)流速沿程逐渐降低，在X=7.0a附近趋于稳定值；压力从汇合管入口迅速上升，在X=4.5a附近增速有所降低，在X=7.0a附近恢复至稳定值；在X=3.5a～7a段紊动能最强，而后逐渐降低。可见，主阀单独运行时，射流在突扩体段流速较高、压力较低、紊动较弱；射流保持较高流速进入汇合管后，对汇合管形成强烈冲击，流速逐渐降低、压力逐步回升、紊动明显增强。说明在景洪工程当前体型下，突扩体长度偏短，主阀射流对汇合管的冲击较强。

图8 主阀轴线沿程无量纲水力特性分布

2.1.2辅阀单独运行

辅阀单独运行时，阀门段流场结构见图9。由图9可知，由于突扩体长度较短，辅阀射流将直接冲击突扩体迎流面，形成壁面冲击射流及近壁绕流。水流汇入汇合管时，在管口附近形成明显的流速梯度，由于管口两侧流速梯度较大，于辅阀出流侧形成了稳定的涡旋区。可见，辅阀单独运行时，射流在突扩体段存在明显的偏流现象，且偏流强度随辅阀流量的增加而增强；辅阀偏流斜入汇合管后，在汇合管入口附近将形成稳定的涡旋低压区，且最低压力随辅阀流量的增加不断降低。

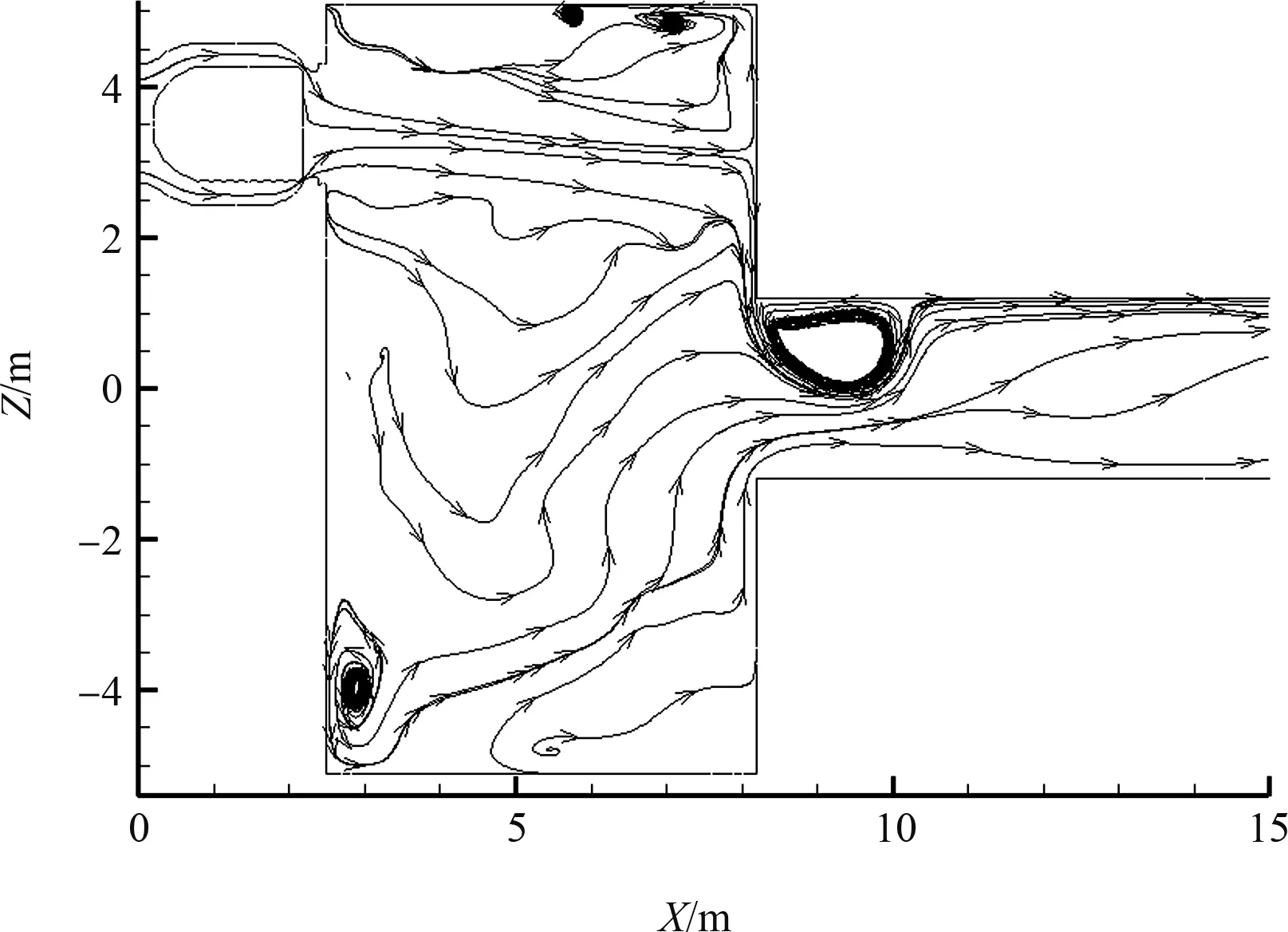
图9 辅阀单独运行时阀门段流场结构

2.1.3一主一辅联合运行

图10 主阀与1台辅阀联合运行时阀门中轴线沿程水力特性

2.1.4三阀联合运行

三阀联合运行时，主阀中轴线沿程水力特性的无量纲分布见图11。由图11可知，在突扩体段(X=0～3.5a)，主阀射流沿程均保持较高流速，各工况基本无差别；压力沿程分布较为稳定；紊动能沿程均较小。在汇合管段(X=3.5a～11a)，流量越大，主阀轴线沿程流速下降越快，在X=7a附近达到稳定值；汇合管内紊动较强。可见，三阀联合运行时，阀门段流场结构较为稳定，阀门单独运行时存在的突扩体段压力过低与偏流现象均得到了明显改善。

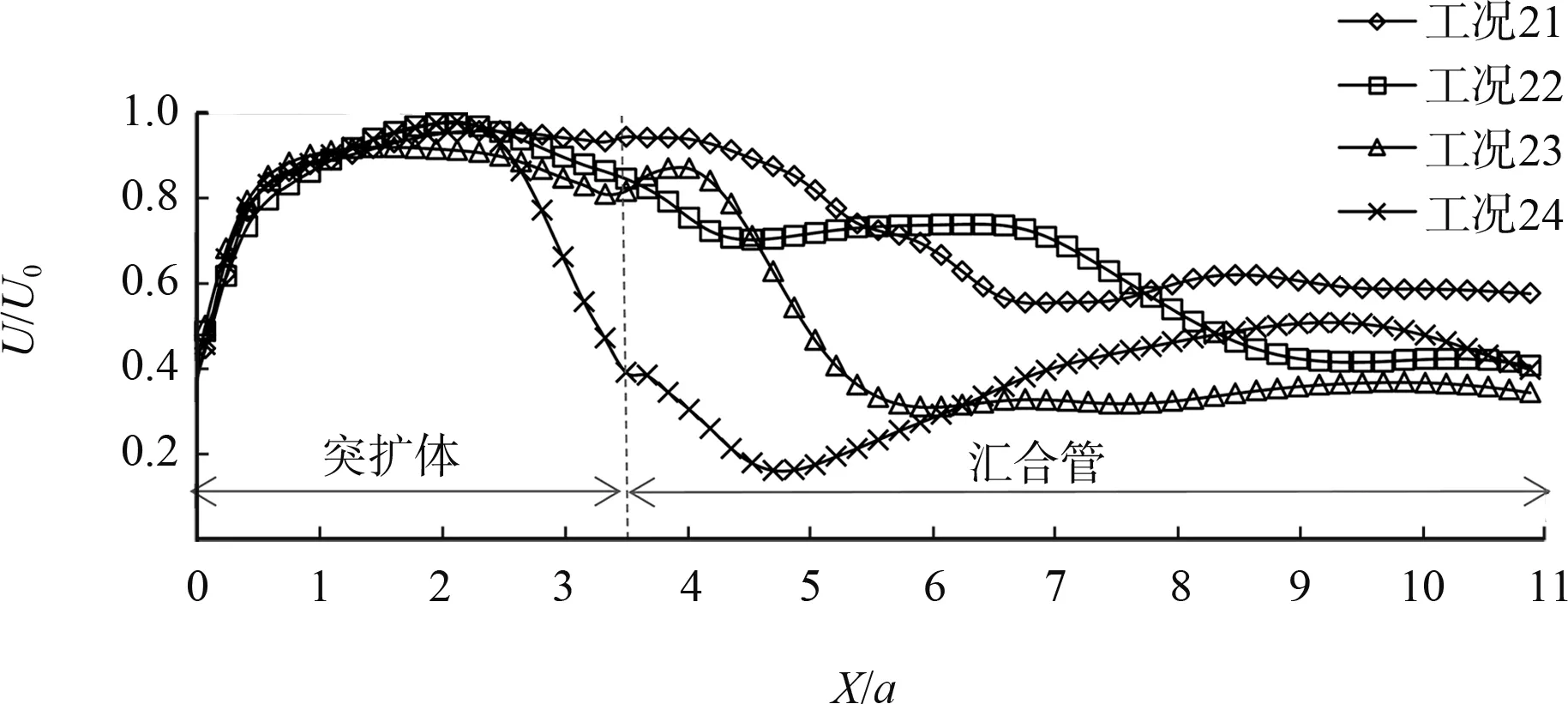
图11 三阀联合运行时主阀中轴线沿程水力特性

2.2 流场均匀度分析

为定量分析组合阀不同运行方式下阀门段流场均匀性的具体差异，用阀门段横向剖面的3条横轴线(X=0.5a、2.0a和3.5a)来代表阀门段内部流场，以流场内最大流速(Uo)和阀门通径(a)为比尺，对各运行方式下的流速分布进行无量纲分析，计算其均匀度(离散系数)，讨论组合阀运行方式与流场均匀性的关系，确定组合阀的最优运行方式。

其中，流场均匀度由离散系数Cv来表征：

(4)

(5)

(6)

离散系数可用于对比均值不同的数据列的离散程度，适用于分析流场的均匀性。离散系数越小，代表均匀度越好。基于流速无量纲化结果，可对每一工况流场特征轴线进行均匀度计算，结果见表3。

由表3可知，各组合阀运行方式下，随着流量的改变，流场典型轴线的均匀度变化不大，说明流场结构的稳定性，具有代表性；而各组合阀运行方式下流场均匀度的整体差异性则说明了不同运行方式与流场均匀性的对应关系。主阀单独运行时，流场典型轴线均匀度变化范围为0.9～2.3；辅阀单独运行时，流场典型轴线均匀度变化范围为0.7～2.6；辅阀联合运行时，流场典型轴线均匀度变化范围为0.3～1.7；主阀与1台辅阀联合运行时，流场典型轴线均匀度变化范围为0.6～1.6；三阀联合运行时，流场典型轴线均匀度变化范围为0.6～1.1。可见，不论是均匀度的变化范围还是数值大小，在所有运行方式中，三阀联合运行时流场的整体均匀性最佳。

表3 组合阀典型运行方式下流场特征轴线均匀度统计

3 结语

1)主阀单独运行时，射流在突扩体段的流速较高、压力较低、紊动较弱；射流保持较高流速进入汇合管后，对汇合管形成强烈冲击，流速逐渐降低、压力逐步回升、紊动明显增强。说明在景洪工程当前体型下，突扩体长度偏短，主阀射流对汇合管的冲击较强。

2)辅阀单独运行时，射流在突扩体段存在明显的偏流现象，且偏流强度随辅阀流量的增加而增强；辅阀偏流斜入汇合管后，在汇合管入口附近形成稳定的涡旋低压区。辅阀联动时，阀门段流场结构的对称性较辅阀单独运行时明显增强。

3)一主一辅联动时，阀门段流场结构与流量比相关。主辅阀流量比≈3:1，是阀门段流场结构转变点；主辅阀流量比>3:1时，主阀射流将主导流场结构，辅阀流量的改变对阀门段流场的影响甚微；主辅阀流量比<3:1时，主辅阀射流间的相互作用明显增强，阀门段流场稳定性将被破坏。

4)三阀联动时，两侧辅阀同时出流，增强了流场的对称性。基于组合阀不同运行方式下的流场典型轴线流速无量纲分布及均匀度分析可知，三阀联动时的流场均匀度最好，是组合阀最佳的运行方式。