基于深度学习理念的高中物理问题的思考与探究——以电磁驱动中的受力与能量问题为例

张石友 时子豪 于虎

(北京市第一七一中学 北京 100013)

1 问题的背景

高中阶段，我们把有关电磁感应的问题大致分为两大类，动生电磁感应类型和感生电磁感应类型．我们把由于金属杆或者金属框架与磁场发生相对运动(或者说由于面积S的变化)从而引起闭合回路磁通量的变化而产生感应电流的现象，称为动生电磁感应现象．

在动生电磁感应现象中，广泛涉及到动力学、电路、能量、动量、宏观与微观结合等问题，可以说为高中物理知识和能力的综合考查提供了良好的平台，因此在历年的高考、模拟等大型考试中备受出题人青睐，近年来北京高考更是倾向于对物理学科本质进行不断探索，例如：从宏观与微观的角度，分析动生电磁感应现象中的功能关系，以此来考查学生的综合分析、解决问题的能力．但是，作为一种较为特殊的电磁感应现象，电磁驱动类型的问题却很少被考查，笔者从教十数年，也一直对电磁驱动类型问题的实质不甚理解，甚至在一些问题中只能人云亦云、随大流地泛泛而谈．

比如，众所周知的一个二级结论，在动生电磁感应现象中，安培力做负功，且克服安培力做功的大小等于产生的电能，或者说克服安培力做功的功率等于电功率．可以表示为

P电=F安v

然而，在电磁驱动中是否也可以运用这一结论呢？答案显然是否定的！在电磁驱动中安培力是做正功的，只这一点，该结论就已经完全不适用了．怎么办？我们似乎一直以来都是把电磁驱动类型的问题当做一种“特例”来处理的，苦口婆心地教会学生“在电磁驱动类型中，情况特殊，我们要特殊问题特殊处理”．笔者这些年教下来，每次到这里心里都有些发虚，也总是在思考这样一个问题，怎么就特殊了呢？一般的动生电磁感应现象和电磁驱动问题怎么就不能统一呢？到底是不是分析过程中出现了什么疏漏，没有考虑周全呢？为此，笔者基于深度学习理念，对电磁驱动问题进行了深入思考与研究．

2 对电磁驱动问题的深入思考与探究

我们先针对一般的动生电磁感应现象，从宏微结合的角度解释和体会.

2.1 洛伦兹力起到能量转换作用

2.1.1 建立模型

如图1所示，足够长的光滑导轨，左端连接阻值为R的电阻，两导轨间距为L，金属棒ab在两导轨之间部分的电阻为r，当金属棒的速度为v时，金属棒内的自由电子(载流子)会有两个分速度，一是随金属棒向右的速度v，二是沿金属棒方向的定向飘逸速度u，而其合速度斜向右下方，如图2所示．

图1 导体棒切割模型

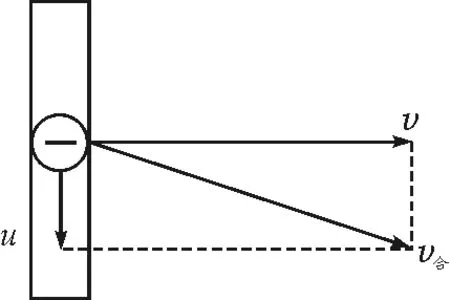
图2 自由电子速度矢量图

2.1.2 问题探讨

(1)从微观角度分析自由电子受洛伦兹力的情况

自由电子因两个分速度而具有的两个洛伦兹力分力如图3所示，分别为f1=evB，f2=euB，而其洛伦兹力的合力为f．(可以证明f的方向和速度v的方向垂直，在此不做详细说明)

图3 自由电子f洛矢量图

(2)分析两个洛伦兹力的分力分别做功的情况

设在极短的一段时间Δt微元内，分力f1做功W1，分力f2做功W2，则有

W1= +f1uΔt= +evBuΔt

W2= -f2vΔt= -euBvΔt

2.1.3 结论

由上述分析可得W1+W2=0，这也恰好佐证了洛伦兹力不做功，只是通过两个分力做功，起到将机械能转为等量电能的“中介”的作用．(其中，沿棒方向分力f1为电源内部的非静电力，做正功，宏观上表现为电源电动势，产生电能；垂直于棒分力f2，宏观上表现为安培力，做负功，消耗机械能)

2.2 在电磁驱动情景中自由电子受力以及能量转化问题

接下来依照上述思路，从宏微结合的角度解释分析．

2.2.1 建立模型

如图4所示，足够长的光滑导轨，左端连接阻值为R的电阻，两导轨间距为L，磁场的磁感应强度为B，当磁场以向右的速度v1匀速运动时，金属棒随之运动，其速度为v2，导轨与金属棒内阻忽略不计．

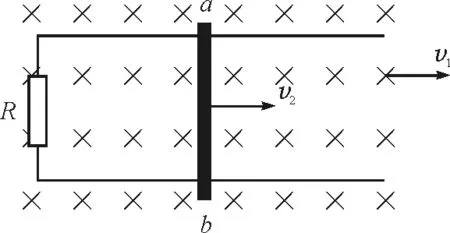
图4 电磁驱动模型

2.2.2 问题探讨

(1)从微观角度分析自由电子受洛伦兹力的情况

根据右手定则可以判断，金属棒的a端为电源负极，b端为电源正极，其内部电流方向为由a向b．则载流子(自由电子)的定向飘逸速度为u，方向为由b向a．同时，金属棒内的自由电子随金属棒向右的速度v2，其合速度斜向右上方，即所对应的金属棒内某个自由电子受到的洛伦兹情况则如图5所示．依然可证洛伦兹力不做功．

图5 电磁驱动中自由电子受力问题

(2)对金属棒感应电动势进行剖析

如图6所示，选取运动参考系S′，它相对于导轨也以速度v1沿与导轨平行的方向运动．在此参考系中，导轨以速度v1向左运动，金属棒稳定运动时以(v1-v2)向左运动．考虑到不同参考系中所表现到的电磁场情况并不一样，对于一个参考系中的纯磁场，在另一个参考系中看来，还将会有可能存在电场．根据非相对论情形(v≪c)下的电场和磁场的变换式[1]

E′=E+v×B

可得感生电场强度和磁场强度的分量如下

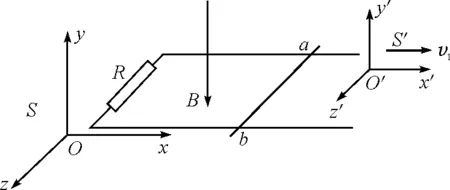
图6 电磁场变换情境图示

因此在S系中可进一步分析自由电子受力，如图7所示，除了洛伦兹力外，自由电子还应受到a指向b的感生电场力，大小为F电=eEz=ev1B，在S系看来，这个感生电场力充当动力作用，使自由电子发生定向移动(定向移动速度为u)，从而形成感应电流[2]．

图7 在S系中分析自由电子受力

E=BL(v1-v2)

(3)从能量转化与守恒视角分析电磁驱动

根据闭合电路欧姆定律

BL(v1-v2)=IR

展开后整理为BLv1-BLv2=IR，我们可以将之进行如下理解：等号左边“BLv1”表示由于磁场以v1运动导致金属棒切割磁感线产生的电动势，称之为正电动势；“BLv2”表示金属棒以速度v2切割磁感线产生的电动势，方向与正电动势相反，故称之为反电动势．因此可以看出在此过程中金属棒的角色既是发电机也是电动机．

闭合电路欧姆定律的实质是能量守恒定律，从能量角度来讲，我们可以将上式等号两侧同时乘以电流I，得

BLv1I=I2R+BLv2I

其中，BLv1I为产生“电能”的电功率，而BLv2I为输出的机械能的机械功率，I2R为电热功率．等式反映了磁场与电路系统的能量转化与守恒关系．

我们也可以把电磁驱动情景与我们熟悉的“一对相互作用的滑动摩擦力对系统所做总功的代数和的绝对值等于因摩擦生热而产生的内能”进行类比，以规律的进阶便于学生理解．滑动摩擦力的作用是阻碍物体间的相对运动，在电磁驱动情境中安培力虽然是动力作用，但磁场运动，金属棒相对磁场反向运动，安培力的作用是阻碍这个相对运动，那么我们可以类比猜想，电路的电能应等于安培力乘以金属棒相对磁场运动的位移即E电=F安x相．论证如下：在电磁驱动过程中，磁场给金属棒一个向右的安培力，与此同时，磁场本身必受到向左的反作用力，为保证磁场速度恒为v1，外界需给磁场一个向右的作用力F，大小等于安培力．那么拉力对磁场做功的功率为

PF=Fv1=F安v1

安培力对金属棒的功率为

P安=F安v2

功率差值为

ΔP=F安(v1-v2)=F安v相

可以看出，F安v相即为电源总功率．