深度建构数学概念的实践与研究

马志浩

一、小学数学概念教学存在的问题

概念教学在小学数学中占据着较大的比例，在教学中，教师只是注重让学生熟练地背诵概念，许多学生在真正运用的时候却不能举一反三，灵活应用。现在存在主要的问题有以下几种。

1.概念之间的联系时常忽略

在小学阶段，许多概念之间是相互联系的，也就是前后都有关联的，如果让学生明白这种联系，可以达到融会贯通的目的。而我们在平时的教学中，并没有前后联系，从而导致学生不能灵活运用。例如：比例尺概念的教学，我们好多教师只是在地图中引入比例尺概念，告诉学生图上比例尺表示的具体含义，如1∶100就是图上距离是实际距离的，然后具体解释，如果图上距离是1厘米，那么实际距离就是100厘米，图上距离是2厘米，那么实际距离就是200厘米……这样教学就是把比例尺概念当作一个全新的概念，孤立地进行教学，没有很好地与原有的概念建立联系，学生学习后也不能灵活运用比例尺的知识。

2.概念的剖析浮于表面

在教学中，我们对概念的剖析，往往是浮于表面的，经常用抽象的文字解释概念的内涵，这对于学生来说是难于理解的。例如，学习“百分数的认识”时，我们常会用一些含有百分数的信息作载体来学习百分数的意义。如衣服的成分，棉占80%，表

示（     ）是（     ）的80%;一班的男生占55%，表

示（     ）是（     ）的55%等。然后通過几个例子归纳出百分数的意义表示一个数是另一个数的百分之几。这样的教学，让学生不能真正的理解。

3.概念的外延简单划一

当我们利用数形结合的策略，剖析数学概念的内涵后，许多教师认为概念教学到此为止，认为学生应该能很好地建构数学概念了。例如，在学习“面积单位平方厘米”时，我们强调边长1厘米的正方形的面积是1平方厘米，这当然没有错，但是仅仅这样还是不够的，学生会片面地认为1平方厘米必须是正方形的面积，事实上，1平方厘米可以是三角形的、正方形的、长方形的面积，甚至是不规则图形的面积。

二、深度建构数学概念的探索

如何让学生深度建构数学概念，而不是仅仅依靠记忆？我们认为，数学概念的深度建构，需要经历感悟—剖析—丰富—厘清的过程。

1.前后连接，感悟概念的联系

数学概念都有它产生的背景，而且概念与概念之间有联系，并不是孤立存在的。所以在引入概念时，要关注概念产生的背景，关注概念与概念之间的联系，让学生明白概念是在什么情况下产生的，它有什么用处，它与哪个已经学过的概念有联系等，从而感悟概念之间的联系，达到融会贯通的目的。

例如，“图形的放大与缩小”一课中，学生知道了图形按相同的比来放大或缩小，才会和原来的图形比较像，而这一原理正是比例尺产生的原因。基于这样的思考，笔者让学生经历寻找相同比的过程，从而深度建构比例尺的概念。这是让学生体会比例尺产生的过程，在找相同比的过程中初步感受比例尺的概念。

2.数形结合，剖析概念的内涵

在初步感悟概念之间联系的基础上，就要深入剖析概念的内涵。剖析概念的内涵，仅仅从数或形某一方面来进行，都是比较片面的，只有数形结合，才能引导学生深度建构数学概念。以形示数，使数得以直观化;以数助形，使形得以数量化。两者结合，才能深入理解概念本质。

例如，在学习正比例时，我们让学生观察表格发现规律，然后再出示图像，数形结合，引导学生把握正比例概念的内涵，即两个变化的量，相应的比值一定，我们就说这两个量成正比例。

3.变式比较，丰富概念的外延

在教学中，我们常常会发现，学生好像已经掌握了相关的概念，但只要稍一变化，学生就糊涂了。例如，认识直线后，我们再出示一条斜着画的直线，学生就会认为这不是直线。这是因为学生对概念的外延不清晰。为了化解这样的问题，依据顾泠沅老师的“变式”理论，我们在教学中不仅应用标准变式，也有意识地引入一些“非标准变式”，以帮助学生深度建构。

如在“面积和面积单位”一课中，学生学习了1平方厘米后，就有如下活动：

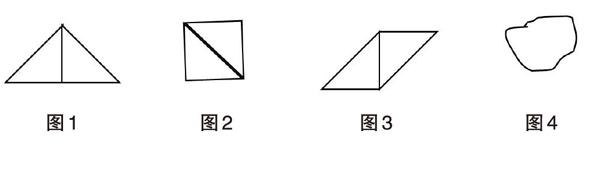
（1）将1平方厘米的正方形沿对角线剪开，变成2个半平方厘米的三角形，让学生用这两个三角形来拼，看看可以拼成什么图形？

在反馈交流时，有的拼成了一个大三角形（如图1），有的拼成了一个正方形（如图2），也有的拼成了一个平行四边形（如图3），并进一步引导学生发现，这些图形形状不同，周长不同，但面积都是1平方厘米。

（2）接着再让学生估计图4这个图形的面积大约是多少平方厘米？（1平方厘米）在估计的过程中，学生不仅建构了规则图形的1平方厘米，同时也建构了不规则图形的1平方厘米，进一步丰富学生头脑中1平方厘米的表象。因为在我们的生活中，更多的是不规则的图形。

（3）在建构了1平方厘米的表象后，我们再让学生建构2平方厘米、5平方厘米和10平方厘米的表象，在这样进一步的变化与推进中，我们让学生把握了平方厘米这个概念的本质。

引导学生理解概念的内涵，在各种标准变式与非标准变式图形中，我们用举例的方式向学生展示概念的外延，使学生辨析的过程中，丰富了概念的外延，促进学生深度建构数学概念。

4.整体梳理，厘清概念的体系

在概念的学习中，学生往往会将许多概念孤立开来，不会主动地去发现概念与概念之间的联系与区别，从而不会灵活地运用所学的概念，也就不能将所学的知识连接成网了。如果在学习概念时，我们能进行整体梳理，既梳理概念与概念的联系，又梳理概念与概念的区别，从而厘清概念的体系，从整体上建构概念网络，最终实现深度建构数学概念的目的，从而灵活运用，举一反三。

综上所述，当我们以发展的眼光来看待一个数学概念，自然而然就会去关注这个概念产生的背景，概念间的联系，剖析概念的内涵，丰富概念的外延，整体建构概念体系，从而深度建构数学概念，让学生学得扎实、灵活、有效。

（作者单位：浙江省杭州市余杭区崇贤第一小学）

责任编辑：高珊

1040756279@qq.com