多传感器非线性系统的鲁棒SCI-UKF滤波器

周 晗，孙小君,2,*

(1.黑龙江大学 电子工程学院，哈尔滨 150080；2.黑龙江省信息融合估计与检测重点实验室，哈尔滨 150080)

0 引 言

非线性系统是生活中广泛应用的系统，它应用于船舶导航、卫星轨道姿态估计、车辆违规测速或雷达探测等系统[1-3]。非线性系统由于微积分的计算复杂，往往不能直接求得精确的最优解。为此，相关学者提出了多种近似的非线性滤波方法[1-3]。文献[5-6]提出了扩展Kalman滤波(EKF),通过对非线性系统模型进行泰勒展开，将其近似转化成线性系统，再套用线性系统的Kalman滤波方法，由于省略了高阶项，从而产生模型误差，严重还会导致滤波发散。文献[7-8]提出了无迹Kalman滤波(UKF)，不需要对非线性系统进行线性化近似，可避免非线性函数雅克比矩阵的复杂运算，保证了非线性系统的普遍适应性，此外还使得高斯噪声得到抑制，其精度相当于二阶泰勒展开，但相较于EKF算法其运行速度会略慢一些[9]。

多传感器信息融合是把多个相同或不同类型的传感器或信息源所提供的局部数据或信息加以综合、组合、融合，得到系统状态更精确的估计[10]。近几十年来，多传感器信息融合已经受到了广泛关注并被应用到导航、卫星定位、无人机、目标跟踪和信号处理等许多高科技领域中，其中信息融合滤波理论是多传感器信息融合的一个重要分支，主要集中于研究多传感器信息融合Kalman滤波[1-3]。文献[11]首次提出了协方差交叉(CI)信息融合方法，它是一种分布式融合算法。其优点可以避免互协方差的计算，减小计算负担，可扩大信息融合技术适用范围[12]。文献[13]将CI融合技术运用到Wiener滤波器中。文献[14]给出了一种协方差交叉融合鲁棒Kalman滤波器，并证明CI融合器的精度是接近于按矩阵加权最优融合器的精度。文献[15] 针对带未知不确定估计误差方差和互协方差的多传感器融合估计问题，在CI融合的基础上提出许多鲁棒融合Kalman滤波器，如改进的CI鲁棒融合器、批处理协方差交叉(BCI)融合鲁棒估值器、序贯协方差交叉(SCI)融合鲁棒估值器以及并行协方差(PCI)鲁棒估值器。

近年来，对于非线性系统研究不断加深，相关学者不断地将信息融合技术应用到非线性系统中，文献[16]加权观测融合算法与UKF相结合提出加权融合无迹Kalman滤波器。文献[17]则是在文献[16]的基础上采用Gauss-Hermite逼近方法减小其计算负担，但因加权观测融合要求准确的噪声方差，且计算量仍旧繁重。文献[18]将CI融合与粒子Kalman滤波器相结合，用来对非线性系统进行滤波。针对带不同观测阵与未知互协方差的多传感器非线性系统，在UKF滤波方法的基础上，提出SCI融合鲁棒无迹Kalman滤波器，将有效地解决带未知噪声统计的多传感器非线性系统的状态估计问题。

1 问题描述

设离散非线性系统模型的状态方程与观测方程为

x(k+1)=f(x(k),k)+w(k)

(1)

y(i)(k)=h(i)(k)(x(k),k)+v(i)(k),i=1,…,L

(2)

(3)

问题是针对非线性系统，已知其噪声保守上界，提出多传感器非线性系统的SCI融合鲁棒无迹Kalman滤波器。

2 UKF滤波方法实现

UKF滤波方法的基本原理是将UT(unscented transform)变换与经典的Kalman滤波器相结合，其中Kalman滤波方法为非线性高斯滤波提供了一种次优的递推式实现方法[19]。

2.1 UT变换原理

UT变换就是用固定数量的参数去近似代替一个高斯分布，因为在进行Kalman滤波时，每一步的迭代过程中均需要求出随机分布经过非线性变换后的均值和方差，由于近似概率分布要比近似非线性函数更易获得，只需在原状态分布中通过Sigma点采样策略规则取一些采样点，使这些采样点与原状态分布具有相同的均值和协方差。这些采样点也被称为Sigma点，对其的要求是在获取输入变量x的分布特征的条件下，使逼近输出的某些性能指标的代价函数取最小[20]。

(4)

(5)

利用式(3)和(4)获得一组Sigma点集及其对应的权值[8]：

(6)

计算2n+1个Sigma点集的一步预测，l=1，…，2n+1。

x(l)(k+1|k)=f[x(l)(k|k),k]

(7)

(8)

根据一步预测值，二次使用UT变换产生新的Sigma点集：

(9)

2.2 无迹Kalman滤波器

将式(9)带入到观测方程中，得到系统的一步预测观测，此时的l=1～2n+1。

y(l)(k+1|k)=h[x(l)(k+1|k),k+1]

(10)

通过加权求和得到量测输出变量的方差阵:

(11)

计算协方差:

(12)

计算增益矩阵:

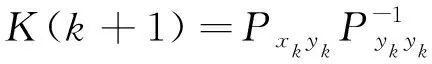
(13)

从而得到无迹Kalman滤波器。

引理 1[9]对于非线性系统(1)和(2)的噪声满足(3)的条件下，无迹Kalman滤波器为

i=1,…,l

(14)

(15)

3 多传感器非线性系统的鲁棒SCI-UKF滤波器

采用的是序贯协方差交叉(SCI)融合，它等价于若干个两传感器协方差交叉(CI)融合器，是一种快速递推的两传感器CI融合器，本质上还是一种按矩阵加权融合器，所以是次优的，其滤波后的精度要小于观测融合[15]。

(16)

(17)

(18)

其中，定义0≤ω≤1，则有

Ω⊃ΩP1∩ΩP2

(19)

则对于任意u∈ΩP1∩ΩP2有

(20)

由于0≤ω≤1，则有

(21)

则引出u∈Ω，故式(19)成立。此时为

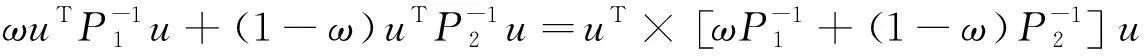
(22)

(23)

则Ω就是PCI的协方差椭圆，即

(24)

(25)

则有

(26)

(27)

(28)

(29)

(30)

将式(28)带入式(29)和(30)即可得到CI融合算法。

定理1对于不确定噪声方差的非线性系统(1)和(2)在满足(3)的条件下，得到的CI融合鲁棒无迹Kalman滤波器(CI-UKF)为

(31)

(32)

证明基于无迹Kalman滤波器式(14)和(15)应用CI融合算法式(29)和(30)，便容易得证式(31)与(32)。

trPCI≤trPi,i=1,2

(33)

序贯协方差交叉融合鲁棒无迹Kalman滤波器(SCI-UKF)主要针对非线性多传感器系统，现将局部传感器1与局部传感器2通过CI-UKF得到的结果再与传感器3进行融合，依次如下，直到第L个传感器参与融合，故其融合精度应高于任意一个局部滤波器的鲁棒精度。在文献[21]中还给出了仿真例子，说明了SCI融合器的鲁棒和其实际精度关于融合的次序不是很灵敏，更加便于实际操作[15]。

SCI-UKF估计原理可用如下L-1步实现：

…

(34)

(35)

重复利用两传感器CI-UKF式(31)和(32)，则SCI-UKF可用L-1个两传感器CI-UKF递推实现[13]。便可证得如下定理。

定理2对于不确定噪声方差的非线性系统(1)和(2)在满足(3)的条件下，便可得到的SCI融合鲁棒无迹Kalman滤波器为

(36)

(37)

4 仿真模型及结果分析

考虑文献[22]中所提具有3个传感器的跟踪系统，其状态方程为

(38)

传感器量测方程为

y(i)(k)=h(i)(x(k))+v(i)(k),i=1,2,3

(39)

为验证本文理论结果的正确性，进行了N=50次Monte-Carlo仿真实验，在时刻k处局部和融合Kalman滤波器的累计均方误差(Accumulated mean square error，AMSE)定义为

(40)

仿真结果如下列各图所示。局部UKF(Local filter 1～3，LF 1～3)与SCI-UKF滤波效果见图1～图4，实线表示真值，虚线表示估值。LF 1～3与SCI-UKF对位置追踪的AMSE曲线见图5，LF 1～3与SCI-UKF对速度追踪的AMSE曲线见图6。由图5可见，传感器2虽然对位置追踪效果较好，其滤波精度甚至略高于融合后的滤波精度，这是由于CI融合其本质上是只一种按矩阵加权融合器，属于一种次优滤波。但通过对比图6可见传感器2在对速度的追踪存在较大的偏差。然而SCI-UKF能同时实现对位置与速度的跟踪，且追踪性能相较于任一局部UKF更加准确，且操作简便，便于实时运用。

图1 局部传感器1的滤波效果图Fig.1 Filter effect diagram of the first local sensor

图2 局部传感器2的滤波效果图Fig.2 Filter effect diagram of the second local sensor

图3 局部传感器3的滤波效果图Fig.3 Filter effect diagram of the third local sensor

图4 SIC融合鲁棒UKF滤波效果图Fig.4 Effect diagram of SCI-UKF

图5 局部UKF与SCI-UKF对位置的ASME曲线Fig.5 AMSE curves of local UKF and SCI-UKF location tracking

图6 局部UKF与SCI-UKF对速度的ASME曲线Fig.6 AMSE curves of local UKF and SCI-UKF velocity tracking

5 结 论

对带不确定噪声的多传感器非线性系统，应用SCI融合算法，提出一种基于SCI融合鲁棒无迹Kalman滤波器。融合算法的引入，极大提高了噪声统计不确定条件下，多传感器非线性系统的状态估计的精度。一个带不同观测阵的3传感器二维跟踪系统的实例也表明了所提出的算法的有效性和可行性。