平底突扩三元水跃流场的数值模拟

宁利中，张 珂，宁碧波，渠亚伟，田伟利

(1.西安理工大学省部共建西北旱区生态水利国家重点实验室，西安 710048；2．嘉兴学院 建筑工程学院，浙江 嘉兴 314001；3．上海大学 建筑系，上海 200444)

0 引 言

水利枢纽的建设改变了原河流中水流的流态，当水流经过水闸时，下泄水流携带着较大的机械能，常伴有空化、空蚀、冲刷及雾化等不良的水力学问题[1]。消能工能够起到促使流体通过发生紊乱而以热能的形式来减少水流机械能和保护下游河床的作用[2-3]。所以选择适宜的消能方式和消能工的合理布置是水利枢纽能够安全运行的保障[4-5]。

底流消能作为传统消能形式之一，其优势明显。底流消能具有对地质条件的适应性较高，对河床冲刷小，泄洪雾化很小，消能率较高等优点[6]。目前国内的一些水利枢纽采用了底流消能形式，如亭子口水利枢纽[7]的5个底孔、恰甫其海水电站[8]的中孔泄洪洞和导流洞、还有葛洲坝二江泄水闸[9]，国外具有代表性的工程有特里水电站大坝[10]、萨扬舒申斯克水电站[11]等。

在排水行洪期，多孔闸门全部启用，可能会产生经典二元水跃，但在多数情况下，为部分闸门对称开启，闸后水流在突扩处开始向两侧扩散，水流会互相混掺碰撞，形成一种水面波动大，水面线难以确定的复杂三元突扩水跃。闸后水流在经过突扩断面时流速减小，会对上游水流的下泄产生一定的阻碍和顶托作用，从而使得水面线壅高，当上下游水深达到共轭水深关系时，就会产生水跃现象，水利工程上常利用水跃进行消能，即底流消能。国内外对棱柱体渠道内的二元水跃和渐扩式渠道内的三元水跃已做了大量研究，罗永钦[12]结合物理模型试验和三维数值模拟，得到了适宜观音岩水电站突跌渐扩式溢流坝消力池体型。一些学者指出，渠道的突然收缩或扩散能够使水流在一定范围内剧烈紊动，可以作为消能的主要手段[13]。但是对于平底突扩三元水跃的研究相对较少。韩伟濛等[14]以某一水利工程为原型设计并进行了物理模型试验，对水跃跃尾水深的计算公式进行了修正。文献[15-19]对平底突扩式渠道内的回流区水深提出不同假设，通过动量方程推导出更高精度的共轭水深计算公式。对突扩水跃的分类有着不同的标准，Rajaratnam等[20]以下游水位与产生水跃的形式将水跃分为R水跃和S水跃。Bremen等[21]以水跃发生的位置将平底突扩渠道中的水跃分成了R型水跃、S型水跃、T型水跃和经典水跃。文献[22-24]对水跃的紊流特性，掺气特性进行了测量与直接数值模拟。本文基于前人所做试验成果，对平底突扩式渠道中发生的S型淹没式水跃，S型临界式水跃和R型水跃进行了三维数值模拟计算，旨在总结平底突扩三元水跃的流速、流线、紊动能和最大流速等水力特性。

1 数学模型

1.1 控制方程

连续方程为

(1)

动量方程为

(2)

雷诺应力方程为

(3)

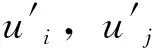
较标准k-ε模型而言，RNGk-ε模型能够更好地模拟这种对流线曲度较大的流动，本文采用RNGk-ε来封闭流体力学方程。

湍动动能k方程为

(4)

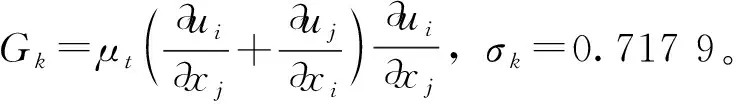
湍动动能耗散率ε方程为

(5)

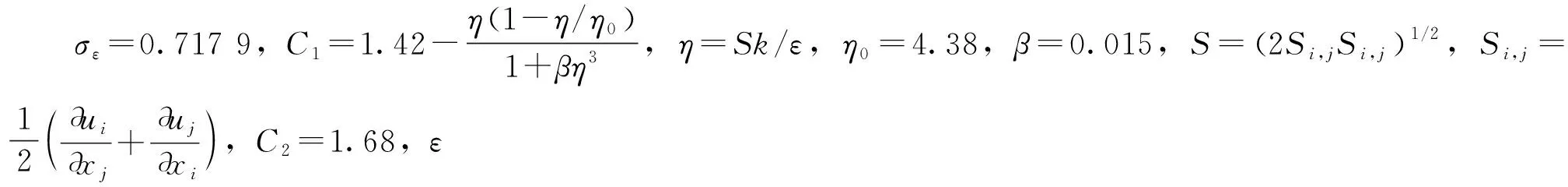
联合以上方程组，针对实际问题给定相对应的边界条件，便可定量求解。

1.2 VOF法

VOF法的基本思想是:定义一个表示计算区域内流体体积与计算区域总体积的相对比例的体积率函数Fw(xi,t)=1。对于某一具体计算单元而言，当函数值为1时，表示单元完全被液体充满；当函数值为0时，表示一个空单元；若函数值介于0和1之间时，表示液体占单元的一部分。

描述的控制方程为

(6)

引入VOF后，ρ，μ为Fw(xi,t)的函数，其表达式为

ρ=Fwρw(1-Fw)ρa

(7)

μ=Fwμw(1-Fw)μa

(8)

式中：ρw和ρa分别为水和空气的密度；μw和μa分别为水和空气的分子粘性系数。

1.3 计算模型

基于卢士强[25]试验，建立三维平底突扩水跃计算模型(图1)，模型中突扩口至上游始端的距离和下游河道末端的长度分别为0.50 m和3.00 m，上下游侧墙高分别为0.50 m和0.40 m，上、下游河宽分别为0.15 m和0.30 m，即扩散比为2.0。模型主要分为闸室段和下游扩散段。突扩口在计算模型的位置为x=0.00 m(yz平面)，上游x为负值，下游x为正值。

图1 三维平底突扩水跃计算模型(单位：m)Fig.1 Calculation model of 3D hydraulic jump with flat bottom and abrupt lateral expansion

1.4 计算工况

对扩散比为2.0下的体型做了数值模拟计算。已知条件：闸门开启高度为0.03 m，上游水位为0.44 m，跃前水深为0.025 m，跃前流速为2.53 m/s，跃长为0.90 m。再通过改变下游水位(h2=0.09，0.13，0.17 m)，使得水跃逐渐由R型水跃过渡到S型临界式水跃，再变化到S型淹没式水跃，从而实现水跃过程的变化。

1.5 边界条件

边界条件如下：进口为流速进口，在计算时给定上游水位0.44 m，并给定一个行进流速；出口为压力出口，给定一个下游水位(h2=0.09，0.13，0.17 m)，并且下游出口处的水流为缓流，服从压力静态分布；模型上部空气为压力进口，进口断面最顶部工作压强设为101 325 Pa；侧面和底面为无滑移固体壁面。

1.6 计算方法

采用VOF法进行自由表面的追踪计算，流体力学气液两相流时均方程采用RNG模型进行封闭，控制方程采用有限体积法进行离散，速度与压力耦合方程采用PIOS算法进行求解。时间步长为0.01 s，收敛标准为进出口质量流通率的差值与进口质量流通率之比≤1%。

利用Fluent软件，采用非定常流动PISO算法，对平底突扩三元水跃进行了数值模拟计算。

2 计算结果及分析

2.1 计算模型的验证

高远[26]以卢士强[25]所做试验数据为基础，利用FLOW-3D软件对平底突扩三元水跃进行了数值模拟计算。本文对闸门开启高度为0.03 m，上游水位为0.44 m的工况时S型临界式水跃，利用Fluent软件进行了数值模拟，提取计算了x=0.10 m，x=0.65 m，x=1.10 m位置横截面中垂线的流速平均值的计算结果并与高远所做数值模拟计算结果进行对比，对比结果见表1。

表1 不同横截面的平均流速对比Table 1 Comparison of average velocity for different cross sections

由表1可见，3个位置横截面中垂线的平均流速值相近。另外，本文计算的S型临界式水跃对应的下游水位为0.13 m，跃尾位置在x=0.90 m附近，并经计算得到跃尾断面的平均流速为0.43 m/s，与卢士强所做试验结果也相吻合。可验证本文建立的计算模型是正确的。

2.2 计算结果及分析

2.2.1 流线分布

绘制3个工况下中轴立面对应的流线图，见图2。由图2可见，水跃发生的跃首位置。在沿程方向，3个工况下水流均发生了不同程度的水平旋滚，但旋滚的位置不同。流线的疏密情况反映出流速的大小，流线密的区域对应的流速大。水流经过突扩断面后，由急流向缓流转变的过程中发生了水跃，在水跃发生区域，水深沿程逐渐增大，在水流的上部区域形成逆时针方向的翻滚漩涡，空气进入漩涡中，使得主流与旋滚的水流发生碰撞，从而实现能量交换与损失，该区域为水跃的主要消能区。

S型临界式水跃(h2=0.13 m)z=0.024 m平面的流线图见图3。由图3可见，水流经过突扩断面后向两侧发生了几乎对称的扩散运动，在靠近突扩口处，左右两侧水流形成了回流，主要发生在x=0 m断面至x=0.20 m断面之间，回流区的范围不大。扩散后的水流经过渠道侧壁的阻碍作用，折冲挤压主流，主流的流线加密，主流的流速有所增加，在x=1.00 m断面至x=1.30 m断面形成了漩涡，漩涡在左右两岸基本对称分布。从x=1.50 m断面开始，水流平稳。这里在x=1.00 m断面至x=1.30 m断面之间漩涡的不对称可能是主流摆动引起的结果。

2.2.2 紊动能分布

3个工况下中轴立面紊动能分布见图4。由图4可见，在水流表面均形成了一个有空气掺入的翻腾回旋滚动，水流内部产生强烈的摩擦与掺混作用。紊动能表示流体紊动的程度，流体之间的剪切、摩擦混掺、碰撞作用越剧烈，紊动能值越大。紊动能的最大值均在水跃中部，且紊动能由旋滚区的内部向外部逐渐减小。R型水跃发生紊动的范围主要在从突扩口向下游x=1.00 m，z=0.10 m内，最大值为0.35 m2/s2；S型临界式水跃发生紊动的范围较大，主要是在从突扩口向下游x=1.00 m，z=0.16 m内，最大值为0.20 m2/s2；而S型淹没式水跃发生紊动的范围最小，主要是在突扩口向下游x=0.80 m，z=0.10 m内，最大值为0.20 m2/s2。

R型水跃和S型淹没式水跃相比，前者发生的紊动能较大，但水跃发生的范围较大；S型临界式水跃和S型淹没式水跃相比，两者的紊动能相近，但后者水跃发生的范围较小。

2.2.3 流速分布

3个工况下中轴立面流速分布沿程变化图见图5。由图5(a)可见，流速在水跃区各断面从底板开始逐渐增大到最大值Umax，然后逐渐减小；由图5(b)可见，在x=0.60 m断面之前，流速在水跃区各断面从底板开始逐渐增大到最大值Umax，然后逐渐减小到零，之后向上游反方向增加；在x=0.90 m断面，流速在水跃区各断面从底板开始逐渐增大到最大值Umax，然后逐渐减小；由图5(c)可见，在x=0.90 m断面之前，流速在水跃区各断面从底板开始逐渐增大到最大值Umax，然后逐渐减小到零，之后向上反方向增加；在x=1.20 m断面，流速在水跃区各断面从底板开始逐渐增大到最大值Umax，然后逐渐减小。

图5 3个工况下中轴立面流速沿x轴变化Fig.5 Velocity distribution of vertical section of central axis along x-axis under three working conditions

按照边界层理论，边界层厚度δ为各断面上流速最大值至底板的间距。图5(a)中，在x=1.20 m断面之前，边界层厚度δ沿程变化不大，大致在0.01 m高度，在x=1.20 m断面之后，边界层厚度δ逐渐增大到水面附近。图5(b)中，在x=1.20 m断面之前，边界层厚度δ沿程略有增加，但增加趋势平缓，在x=0.90 m断面之后，界层厚度δ逐渐增大到水面附近。图5(c)中，在x=1.20 m断面之前，边界层厚度δ沿程逐渐增加，增加趋势明显，在x=1.20 m断面之后，边界层厚度δ逐渐增大到水面附近。

横断面上流速分布规律为：R型水跃，水跃区内，边界层厚度的变化不大，之后在水跃区向明渠均匀流过渡的过程中变化明显，且逐渐增大到水面附近；S型临界式水跃区内，边界层厚度的逐渐增大，但增加趋势不明显，之后水跃区向明渠均匀流过渡的过程中变化明显，且逐渐增大到水面附近；S型淹没式水跃区内，边界层厚度的逐渐增大，且增加趋势明显，之后水跃区向明渠均匀流过渡的过程中逐渐增大到水面附近。

提取3个工况下的z=0.012 m平面x=0.10 m和x=0.64 m 2个位置的流速分布见图6。

由图6(a)可见，R型水跃的流速整体上最大，S型临界式水跃次之，S型淹没式水跃最小，但流速分布规律相同，因为侧壁为无滑移壁面，在壁面处流速为零。在靠近两边侧墙附近的一定距离内为副流区，其流速比主流区要小，呈现出向上游凹陷分布；由图6(b)可见，R型水跃的流速整体上依然最大，S型临界式水跃次之，S型淹没式水跃最小，但S型淹没式水跃的流速分布趋于均匀。3个工况下副流区范围都有所增大，主流区减小。

图6 3个工况下不同x时在z=0.012 m平面上的流速分布Fig.6 Velocity distribution of z=0.012 m plane at different x under three working conditions

由此得出，R型水跃流速最大，携带能量大，对河床的冲刷最为严重，跃尾位置距突扩口的距离最远；S型临界式水跃流速较小，携带能量较小，流态不稳定，易发生折冲水流，跃尾位置距突扩口的距离减小；S型淹没式水跃流速最小，携带能量最小，流态较为稳定，对河床的冲刷最小，跃尾位置距突扩口的距离最小。

3个工况下横断面最大流速沿程变化见图7。由图7可见，3个工况下，横断面最大流速沿程逐渐减小，不同之处在于：R型水跃，在x=1.50 m处最大流速值变化开始减小，减小到0.8 m/s左右时最大流速趋于平稳；S型临界式水跃，在x=1.20 m处最大流速值变化开始减小，减小到0.6 m/s左右时最大流速趋于平稳；S型淹没式水跃，在x=1.00 m处最大流速值变化开始减小，减小到0.5 m/s左右时最大流速趋于平稳。由此得出：S型淹没式水跃在较短的区域内，最大流速值以较快速率减小，并且区域平稳时的最大流速值相比另外两种工况下要小。

图7 3个工况下横断面最大流速沿x轴变化Fig.7 Variation of maximum velocity of the cross section along x-axis under three working conditions

3 结 论

1)通过对比前人所做数值模拟结果，验证了本文建立的平底突扩三元水跃数值模拟计算模型的正确性，VOF法能够较为准确地跟踪计算自由水面，RNGk-ε湍流模型能够得到在消力池发生水跃的瞬态过程，能够得到一定精度的流速、紊动能等水力特性，表明采用Fluent软件对平底突扩水跃进行三维数值模拟计算具有较强的适用性。

2)得到3种水跃紊动能的分布特点，发现水流紊动能最大值在水跃中部，R型水跃发生的紊动能较大，发生紊动的范围主要在从突扩口向下游x=1.00 m，z=0.10 m内，最大值为0.35 m2/s2；S型临界式水跃和S型淹没式水跃两者的紊动能相同，最大值均为0.20 m2/s2，但是S型临界式水跃发生紊动的范围主要是在从突扩口向下游x=1.00 m，z=0.16 m内，后者主要是在突扩口向下游x=0.80 m，z=0.10 m内。

3)得到3个工况下中轴立面流速分布及边界层变化的特点，发现在相同位置的横断面上，R型水跃流速均较大，R型水跃边界层变化不大，S型临界式水跃边界层增长缓慢，S型淹没式水跃边界层增加趋势明显，最终均增大到水面附近。

4)得到3个工况下z=0.012 m平面沿程流速分布，R型水跃流速最大，跃尾位置距突扩口的距离最远；S型临界式水跃流速较小，流态不稳定，易发生折冲水流，跃尾位置距突扩口的距离减小；S型淹没式水跃流速最小，流态较为稳定，跃尾位置距突扩口的距离最小。

5)S型淹没式水跃最大流速值以较快速率减小，并且最大流速值相比另外两种工况下要小。