基于参数调优Xgboost算法的多余物信号检测技术
李超然,赵娜靖,李 硕,王国涛,2,*
(1.黑龙江大学 电子工程学院,哈尔滨 150080;2.哈尔滨工业大学 军用电器研究所,哈尔滨 150001)
0 引 言
由于我国工业制造水平有限,多余物粒子会在密封继电器生产过程中,封装于内部形成多余物。密封继电器常处在失重,超重等突发冲击的工作环境。内部的多余物粒子会被冲击出来,随机碰撞,当卡在继电器某些关键的器件和组件部位,就会对密封继电器的稳定性和可靠性产生极大的危害,既造成性能的降低,也造成内部电路的短路和异常[1]。
2005年,张辉采用弹性球理论,建立了颗粒碰撞噪声检测的动力学模型,为找到最佳振动试验条件奠定了基础[2]。2006年,高宏亮在前人的基础上研制了基于PIND法的密封电子元器件多余物自动检测系统,实现组件松动的检测[3]。2008年王世成针对军用电子元器件提出了多余物有无的识别方法[4]。2011年针对星载电子设备,乌英嘎从多余物和可动组件的自由度分析,指出多余物脉冲是由强到弱逐渐衰减的过程,而固有机械信号是一个先逐渐上升然后逐渐下降的振动衰减过程,提出采用波形对称度来区分固有机械信号和多余物信号[5]。上述方法在工程应用方面,解决了密封继电器多余物检测技术存在的问题,但是检测的准确度还有待提高。
本次实验将Xgboost算法应用到多余物信号检测技术中,使用网格搜索[6]和k折交叉检验结合的方法,搜索出Xgboost树的最大深度和每棵树随机采样的最好比例,之后使用参数调优的Xgboost算法建立分类模型对密封继电器中的多余物信号和组件信号进行分类。
1 多余物检测信号特征分析
1.1 多余物信号
多余物会在振动台振动的过程中开始在密封继电器内部游离,与密封继电器壁或其内部部件发生碰撞产生能量,该能量会被振动台下方安置的声发射传感器捕获进行转换并输出为电压信号即多余物信号。在整个时间轴上,多余物脉冲信号产生具有随机性,碰撞与尖峰脉冲相对应。多余物脉冲波形见图1。

图1 多余物脉冲时域波形Fig.1 Time domain waveform of the excess pulse
多余物脉冲频域波形见图2。由图2可见,多余物信号频率达到峰值时,会迅速衰减。外部干扰、外部激励条件、多余物的材质、粒径、传输介质等都会影响脉冲的频率特性和形状,因此多余物信号变化没有规律性。

图2 多余物脉冲频域波形Fig.2 Frequency domain waveform of surplus pulse
1.2 组件信号
密封继电器组件信号是在进行PIND实验的过程中继电器内部线路连接和电路板、继电器壁撞击产生的声音由振动台下方安置的传感器转换成输出信号。组件信号是因为继电器的特殊内部构造产生的信号,拥有和多余物信号相似的尖峰脉冲,但是组件信号波形具有周期性,见图3。
由图3可见,在时间轴上,组件信号拥有多余物信号一样的拥有尖峰脉冲的特点,但是组件信号呈现出明显的周期性,组件信号频域波形见图4,可见在时间轴上有一段起振和衰减的过程。
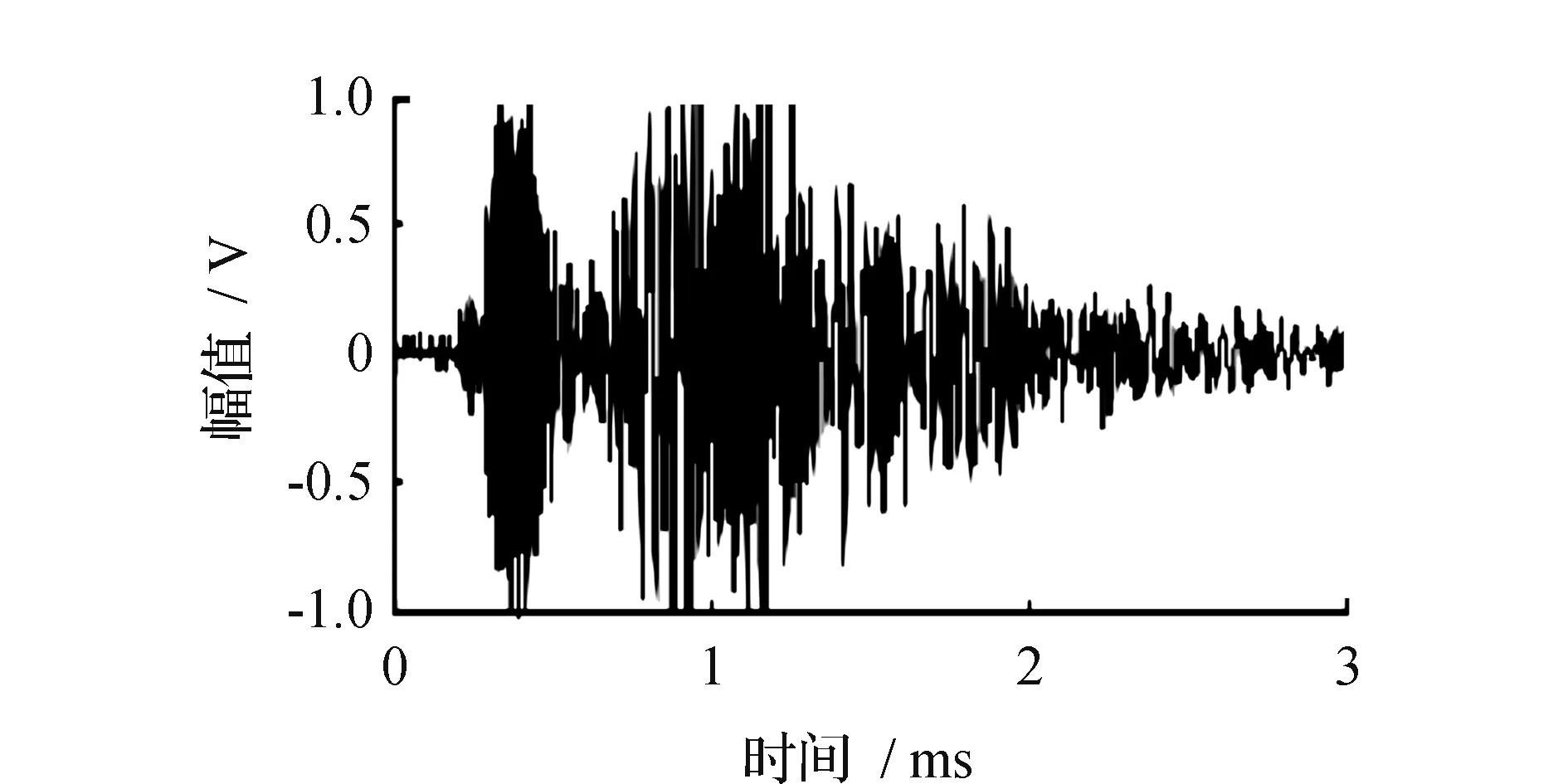
图3 组件信号时域波形Fig.3 Component signal time domain waveform

图4 组件信号频域波形Fig.4 Frequency domain waveform of component signal
由图1~图4可见,组件信号和多余物信号在频域和时域上差别不大。把参考周期设置为外部震动周期,当组件脉冲存在于不同周期时,脉冲发生的时刻基本一致。
因为松动组件的位置基本固定,组件信号中不同脉冲的形状类似,这也是撞击速度不变,传播距离固定,传输介质周期性变化,从而传感器每次接收到的能量一致。松动组件数量是无法确定的,而且多个组件脉冲可能存在于一个振动周期中,组件信号的振动发送不是同步的。在时间序列上,多余物信号脉冲序列的产生呈现不规则性,但是组件信号脉冲序列的产生呈现周期性。
在脉冲波形形状上,多余物不同脉冲的不同波形各式各样,但是组件的脉冲波形相似,多余物信号和组件信号在波形形状上的差别难以区分。
1.3 数据集特征提取与筛选
本次实验使用的是PIND检测系统,为了让密封继电器内部的多余物激活,将系统条件设置为机械冲击,从而给予继电器内部周期性的振荡。激活后的多余物粒子会在继电器空间内部发生碰撞从而产生声音信号,振动台下面安置的有声发射传感器会将其捕捉,然后传输到计算机上将其显示成波形,通过PIND系统内部的程序进行量化,转成数据并将重要的特征参数提取出来。
为了在大量的数据中找出有效的特征,从而压缩空间中的维数,因为不同类的模型点在特征空间中的距离较远,同类模型点的距离较近,可将特征筛选出来。在众多的特征中,每次选择一个特征保持不变,计算其信息增益比,通过信息增益比来衡量分类标签和每个特征之间的相关度。信息增益比是信息增益g(D,A)与训练集D关于特征A的值的熵HA(D)之比。信息增益是以特征A划分数据集D前的熵与划分数据集D后熵的差值,HA(D)的倒数为惩罚因子,特征个数越多,惩罚因子越小;特征个数越少,惩罚因子越大。具体公式如下:
(1)
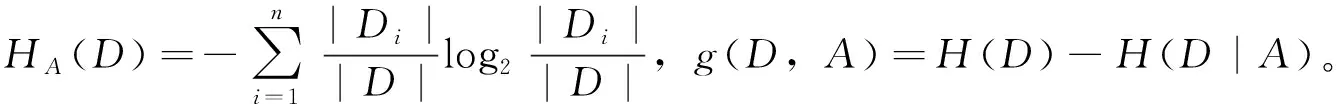
计算每个特征的信息增益进行排序,寻找出所有特征中信息增益高于平均水平的特征,再计算这些特征对应的信息增益率,选取信息增益率较高的特征。特征选择见表1。

表1 特征介绍Table 1 Introduction of features
2 基于参数调优的Xgboost算法
2.1 Xgboost算法
Xgboost是一种集成树模型,是在梯度提升算法的基础上[7-8],将多个弱分类器集成为一个强分类器,其本质是不同的单个决策树的组合[9-10]。因为不是所有的损失函数都是二次函数,所以引入泰勒展开从而进行凸优化,与此同时采用了分布式计算完成了在系统层面的优化。算法步骤如下:
目标函数:
(2)
通过泰勒展开得
(3)
其中:
(4)
(5)
由
(6)
可得
(7)
定义:
Gj=∑i∈Ijgi,Hj=∑i∈Ijhi
(8)
公式化简为
(9)
通过对wj求偏导等于零可得
(10)

(11)
通过以上各式可得一个分隔增益公式:
(12)
2.2 基于网格搜索和交叉检验的Xgboost参数调优
Xgboost算法中树的最大深度max_depth和每棵树随机采样的比例subsample这两个参数对模型性能有很大的影响。但是当前在Xgboost参数调优上还停留在多次实验选出参数的阶段上,这样会导致模型性能不稳定。
针对这个问题,本次实验使用网格搜索和k折交叉检验结合的方法选取最优参数,设定网格范围对(max_depth,subsample)去进行遍历,每组参数对的准确率使用k折交叉检验法去计算,通过最高的准确率进而找到(max_depth,subsample)的全局最优解。具体步骤如下:
1)参数大范围调优。max_depth设定的大范围区间为[1,9],该区间以2为步长,subsample设定的大范围区间为[0.1,0.9],该区间以0.2为步长。这两个区间构成网格,其中每个网格点对应一个(max_depth,subample)参数对。
2)k折交叉检验。使用k折交叉检验的方法,将数据集轮流抽取k-1份作为训练数据,留下的一份作为测试集,去训练每一组参数对应的模型,求出每组模型的准确率。
3)选取大范围的最优参数。针对网格中的每一个交叉点即一个参数对,使用k折交叉检验求出对应参数的模型进行二分类的准确率,选取准确率最高的为当前最优参数记为(max_depthS,subsampleS)。
4)参数小范围调优。把max_depthS上下范围拓展1,subsampleS上下范围拓展0.1。因为之前Max_depth区间步长是2,subsample区间步长为0.2。
5)确定最优参数。重复Step2和step3,二分类准确率最高的模型对应的参数对即为最优参数。
3 实验与仿真分析
3.1 评价指标
Xgboost分类器在测试数据集上的预测是否正确,TP表示将正类预测为正类的样本数量[11-12],TN表示将负类预测为负类的样本数量,FP表示将负类预测为正类的样本数量,FN表示将正类预测为负类的样本数量,本次实验通过混淆矩阵的形式将4种情况列出,混淆矩阵见表2。

表2 二分类混淆矩阵Table 2 Two-class confusion matrix
定义1:准确率:
(13)
准确率越高,分类效果越好,但是在正负样本不均衡的情况下,准确率作为评判标注不合适。需要用precision,recall和f1-measure来评价模型的整体性能。
定义2:召回率:被模型判定为正类占数据集中所有正类的比例。
(14)
定义3:精确率:在被模型判定为正类别的样本中,真实为正类的比例。
(15)
定义4:F-score:精确率和召回率的加权调和平均。
(16)
3.2 实验数据
本次实验通过PIND实验器采集5组实验样本,每组实验样本详情见表3,每组数据由多余物信号数量和组件信号数量组成,正负样本的比例近似为1∶2[13-14]。每组实验样本随机选取3/4样品数据去训练当前要进行调优的模型,剩下的1/4样本数据作为该模型的测试集。

表3 5组样本数据Table 3 Main information of 5 groups of sample data
3.3 实验仿真与分析
3.3.1 基于网格搜索与k折交叉检验结合的调参方法
以分类准确率作为每个(max_depth,subsample)参数对的评价指标,先对参数进行大范围调优即给予max_depth一个1到9的闭区间,以2为步长;subsample一个0.1到0.9的闭区间,以0.2为步长。每个(max_depth,subsample)参数对的准确率见表4。
由表4可见,subsample=0.5,max_depth=9准确率最高,即在这个值附近进行小范围的调优。max_depth的取值区间为[8,10],subsample的取值区间为[0.4,0.6],每个(max_depth,subsample)参数对的准确率见表5。

表4 参数粗调表Table 4 Parameter coarse adjustment table

表5 参数细调表Table 5 Parameter adjustment table
由表5可见,subsample=0.6,max_depth=9附近分类效果比较好。选取subsample=0.6,max_depth=9构建Xgoost模型进行分类验证,对数据采用五折交叉验证进行分类,每组数据重复10次实验,得出各分类指标的平均值见表6。
由表6可见,使用默认参数的Xgboost算法进行二分类时,准确率和精确率均为0.80~0.85,召回率为0.66~0.72,F-score为0.72~0.77。使用调优Xgboost算法准确率则提升到0.88左右,精确率提升到0.86左右,召回率提升到0.80左右,F-score提升到0.84左右。

表6 树的最大深度取9,每棵树随机采样的比例为0.6Table 6 Maximum depth of the tree is 9, and the random sampling ratio of each tree is 0.6
3.3.2 与其他机器算法模型的比较
在密封继电器多余物检测领域,支持向量机算法应用的较为广泛。近几年,集成算法越来越多地被应用到工业领域中,其中GBDT算法和Adaboost算法比较具有代表性[7-8]。本次实验使用5组实验数据,分别采用基于参数调优的svm算法,默认参数的Xgboost算法,Xgboost调优算法[9-10],基于梯度提升决策树(GBDT)算法和基于参数优化的Adaboost算法对密封继电器多余物信号进行判断[11],各算法的准确率和F-score情况见图5、图6。
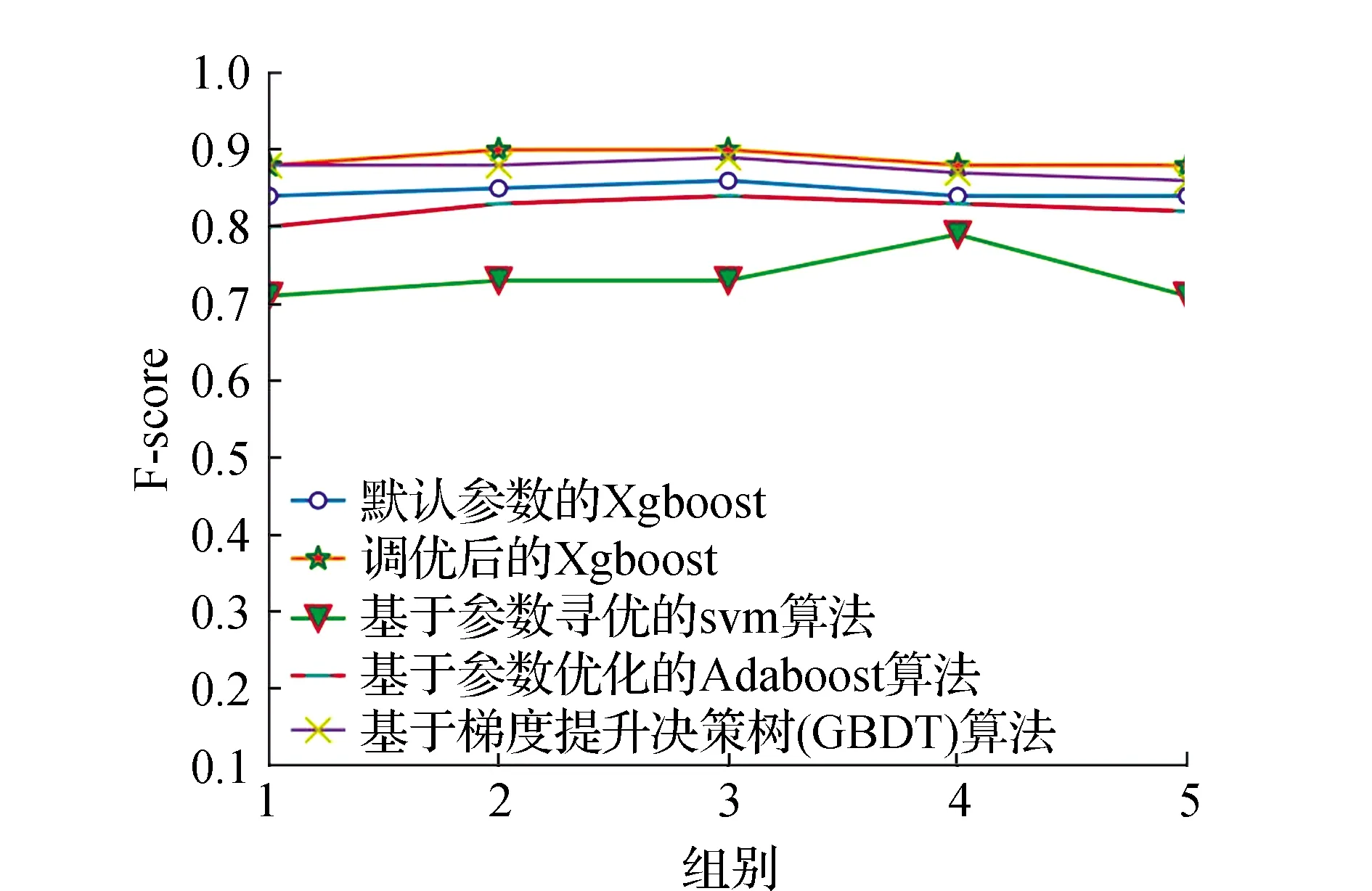
图5 各算法的准确率值Fig.5 Accuracy value of each algorithm

图6 各算法的F-score值Fig.6 F-score value of each algorithm
在本次实验使用的5组数据集中,使用参数为subsample=0.6,max_depth=9构建的Xgoost模型比使用默认参数的Xgboost算法在准确率上最高提升幅度为15%,F-score提升了9%。比当前工业上比较成熟的svm算法在准确率上提升最大幅度为17%,F-score最大的提升幅度为34%。
由图5、图6可见,在多余物数据集上所有集成算法的准确率和F-score都高于现在较为成熟的支持向量机算法,使用基于网格搜索和k折交叉检验结合的方式对Xgboost进行调优在准确率和F-score上都会比基于梯度提升决策树(GBDT)算法和基于参数优化的Adaboost算法有小幅度提升[12],因此在密封继电器多余物信号检测领域,调优后的Xgboost算法能够有效地提升判断的准确率。但是在第4组数据中,调优后的Xgboost算法和基于梯度提升决策树(GBDT)算法的准确率相同,而且在F-score这个评价指标上,使用基于梯度提升决策树(GBDT)算法略优于调优后的Xgboost算法,未来在基于参数调优Xgboost算法的基础上结合其他算法去进一步提高整体算法的性能。
4 结 论
本次实验使用了基于网格搜索和k折交叉检验相结合的方法对Xgboost算法进行参数调优,先进行大范围调优再进行小范围调优解决了参数太多导致耗时长的问题,最终选取Xgboost的树的最大深度为9和每棵树随机采样的比例为0.6,构建出最优模型。通过多组实验数据验证该模型的各项指标优于其自身和其他集成算法,并且比传统的密封继电器多余物信号检测技术有大幅度提升。虽然准确率大幅度提升,但算法要花费更长的时间进行判别。

