卷烟制丝环节关键工序水分预测模型的建立与检验

李自娟 刘 博 高 杨 陈娇娇

(张家口卷烟厂有限责任公司，河北 张家口 075000)

制丝过程中的含水率是卷烟生产中最重要的控制指标，如何尽可能地提高各工序的出口水分控制的平稳性与精准性，一直是各卷烟企业的重点研究内容[1-2]。目前，卷烟制作过程中的松散回潮、叶片加料、热风润叶、薄板烘丝工序多采用PID 算法，以及前馈补偿、顺序逻辑控制手段，这种控制手法的优点是模型简单易实施[3]，但各控制回路间的协调性差，相对独立，较难达到真正的闭环自动控制[4]，实际应用中很难满足动态精度和动态稳定性及平稳性[5]。同时，输出变量与输入变量间具有较强的滞后性[6]。为了提高控制水平，各企业利用大数据技术[7]和计算为基础的机器学习、人工智能等[8-9]技术开展相关研究。钟文焱等[10]建立了基于多因素分析的烘丝机入口含水率预测模型，实现了松散回潮机回潮加水比例自动计算，提高了烘丝机入口含水率稳定性；刘炳军等[11]采用多元回归分析法，研究了烘丝工序各工艺参数间的相关性，提高了批次间的稳定性；董高峰等[12]采用 BP 神经网络模型，研究了烟梗生产的最佳工艺参数组合方案，提高了梗丝质量；王宏铝等[13]构建了烟碱模型，利用模型实时预测原烟烟碱含量，并依据其含量的差异进行分类堆放，实现了均质化加工。

文章拟利用神经网络算法、多元回归分析方法建立松散回潮、叶片加料、热风润叶、薄板烘丝工序等多因素的入口与出口含水率的关系模型，并依据建模方法的预测精度择优选择模型，旨在为借助数据分析提升制丝水分控制精度的目标提供依据。

1 数据与方法

1.1 数据采集及处理

1.1.1 数据采集 选择企业自有卷烟钻石(硬红)，由MES生产管理系统进行数据采集，采集时效3个月。

1.1.2 数据预处理

(1) 预处理1：有效数据筛选。依据3σ原则筛选后[14]，得有效生产记录 192条，其流程为：

开始→统计变量数据→按需求剔除异常样本→形成样本→结束

(2) 预处理2：数据无量纲化，采用极大化法[15]，并分别按式(1)～(7)计算各指标。

c1=t1/30%，

(1)

c2=t2/620，

(2)

c3=t3/80，

(3)

c4=t4/50，

(4)

c5=t5/175，

(5)

c6=t6/50，

(6)

c7=t7/1 250，

(7)

式中：

c1——无量纲含水率；

t1——物料原始含水率，%。

c2——无量纲松散回潮加水量；

t2——原始松散回潮加水量，L；

c3——无量纲补偿蒸气开度；

t3——原始补偿蒸气开度，%。

c4——无量真空回潮到松散回潮时长；

t4——原始真空回潮到松散回潮时长，m；

c5——无量暂存柜储存时长；

t5——原始暂存柜储存时长，m；

c6——无量加料回潮排潮开度；

t6——原始加料回潮排潮开度，%；

c7——无量地下柜储存时长；

t7——原始地下柜储存时长，m。

(3) 预处理3：变量定义。记薄板烘丝机入口水分y，定义变量(无量纲处理后)为：松散回潮入口水分x1、松散回潮出口水分x2、松散回潮加水总量x3、松散回潮补偿蒸气开度x4、真空回潮至松散回潮输送时长x5、暂存柜储存时长x6、加料回潮入口水分x7、加料回潮出口水分x8、加料回潮补偿蒸气开度x9、加料回潮排潮开度x10、地下柜储存时长x11、热风润叶入口水分x12、热风润叶出口水分x13、热风润叶补偿蒸气开度x14。

(4) 预处理4：水分仪零点值修正。各批次水分值根据水分仪零点值进行校正，保证数据在同一零位上，从而保证数据的有效性。

1.2 数学建模

1.2.1 建模方法 将制丝流程进行适当分节，利用神经网络算法、多元回归分析方法建立多因素影响下，每个分节中烟叶或烟丝的入口与出口含水率关系模型；再建立烘丝入口含水率的预测模型，如图1所示。

根据图1所示水分仪的分布，将烘丝前工序分成4段，其中一段：来料至水分仪1；二段：水分仪2至水分仪3；三段：水分仪3至水分仪5；四段：来料至水分仪6。

多元回归法预测模型建立是以历史数据为基础，将目标参数作为y值，其他参数作为变量因子，通过数据代入，得到模型方程。松散回潮工序其变量因子为入口水分、打水量、补偿蒸气开度、真空至松散回潮时长，输出因子为松散回潮机出口水分。同理，其他3个工序以输入因子作为变量，输出因子作为目标值。

神经网络法预测模型建立是通过大量的历史数据，逐步建立和完善输入变量至输出结果之间的路径，通过不同的输入变量值，预测输出结果。各工序模型的建立，采用不同的输入因子、神经元及模型结构，但均采用包含一个隐含层神经网络模型，设定训练目标0.05，训练速度0.01，最大训练步数100。

1.2.2 数据延迟试验 启动生产设备，在工序设备入口处放置标靶，使用秒表开始计时，当标靶运动至设备出口水分检测设备下方时，结束计时。

1.2.3 模型精度试验 同工序水分预测值与对应水分显示值相减，得到模型预测误差。

2 结果与讨论

2.1 工序预测模型构建

2.1.1 多元回归法预测模型的建立 松散润叶工序以入口水分(x1)、总打水量(x3)、补偿蒸气开度(x4)、真空回潮至松散回潮时长(x5)作为变量，以出口水分为因变量，建立多元回归模型，各因子系数见表1。

图1 烘丝前工艺流程

根据表1得：

x2=2.802x1+0.351x3-0.024x4+0.003x5-0.922。

(8)

叶片加料工序以其入口水分(x6)、加料工序暂存柜储存时间(x7)、补偿蒸气开度(x9)、排潮开度(x10)为变量，出口水分(x8)为因变量，建立多元回归模型，各因子系数见表2。

根据表2得：

x8=-0.001x6+0.471x7-0.009x9-0.009x10+0.492。

(9)

热风润叶工序以地下柜储存时长(x11)、热风润叶入口水分(x12)、热风润叶补偿蒸气开度(x14)为变量，热风润叶出口水分(x13)为因变量，建立多元回归模型，各因子系数见表3。

根据表3得：

x13=-0.005x11+0.236x12+0.020x14+0.566。

(10)

以整线影响因素为变量，薄板烘丝机入口水分(Y)为因变量，建立相应的多元回归模型，各因子系数见表4。

根据表4得：

Y=0.306x1+0.037x3+0.001x4+0.002x5+0.002x6-0.065x7+0.004x9-0.001x11+0.006x12+0.004x14+0.583。

(11)

2.1.2 神经网络法预测模型的建立

(1) 松散润叶工序构建松散回潮出口水分神经网络预测模型，其网络结构见表5、6。

表1 松散润叶段各因子系数

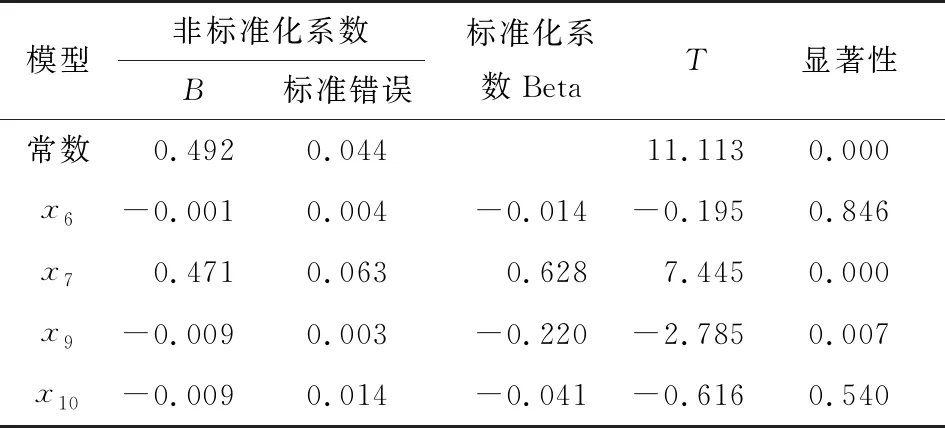
表2 叶片加料段各因子系数

由表5、6可知，该模型为3层结构，输入层为4个因子，输出层为1个因子，神经元为2个，松散回潮入口水分对模型输出值变化最重要(此权重是由建模软件依据参数在模型中对输出结果的贡献值作出的判定)。

(2) 加料回潮工序构建出口水分神经网络预测模型，其网络结构见表7、8。

由表7、8可知，该模型为3层结构，输入层为4个因子，输出层为1个因子，神经元为1个，加料回潮入口水分对模型输出值变化最重要。

(3) 热风润叶工序构建出口水分神经网络预测模型，该网络结构见表9、10。

由表9、10可知，该模型为3层结构，输入层为3个因子，输出层为1个因子，神经元为3个，热风润叶入口水分对模型输出值变化最重要。

(4) 构建整线神经网络预测模型，其网络结构见表11、12。

由表11、12可知，该模型为3层结构，输入层为10个因子，输出层为1个因子，神经元为1个，热风润叶入口水分对模型输出值变化最重要。

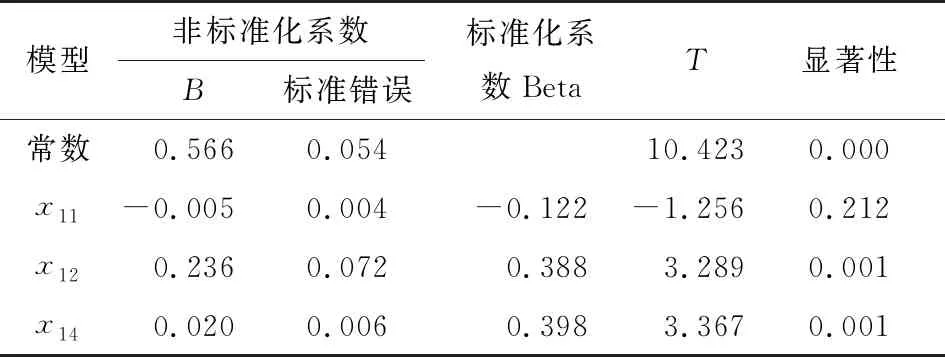
表3 热风润叶段各因子系数

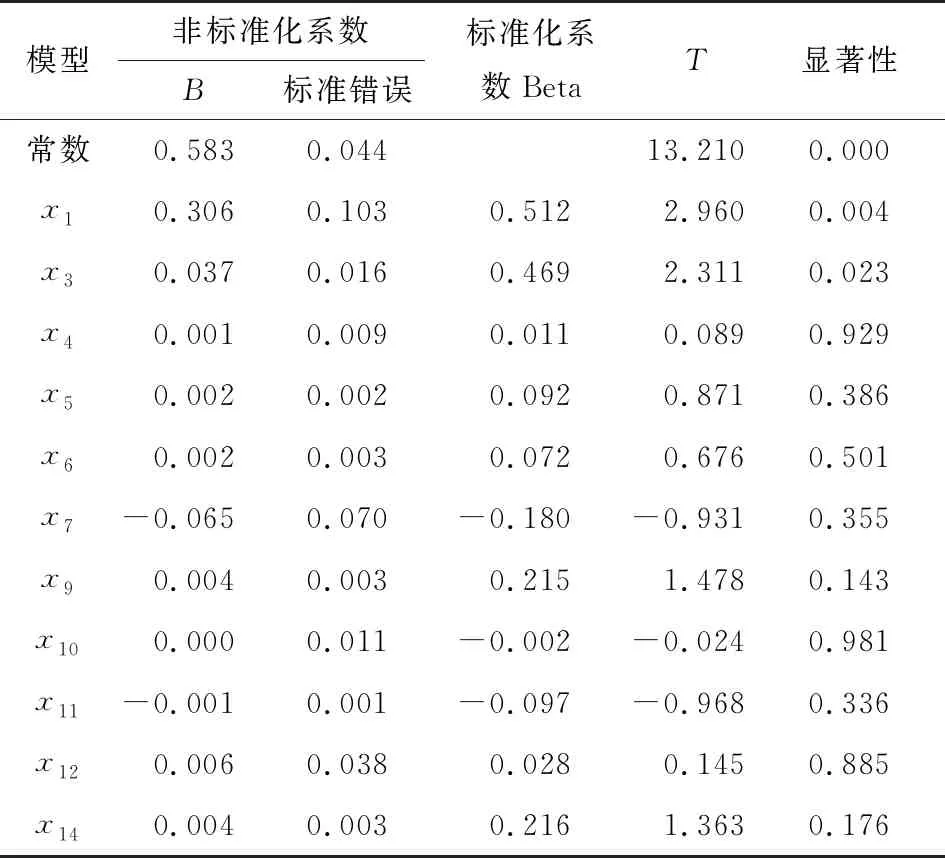
表4 整线各影响因子系数

2.2 工序模型优选试验

两种模型分别对同一生产批次进行预测，并与生产运行实际显示值进行配对T检验，其结果见表13。

由表13可知，松散回潮段选用误差较小的多元回归模型；加料回潮段、热风润叶段及整线选用误差较小的神经网络模型。

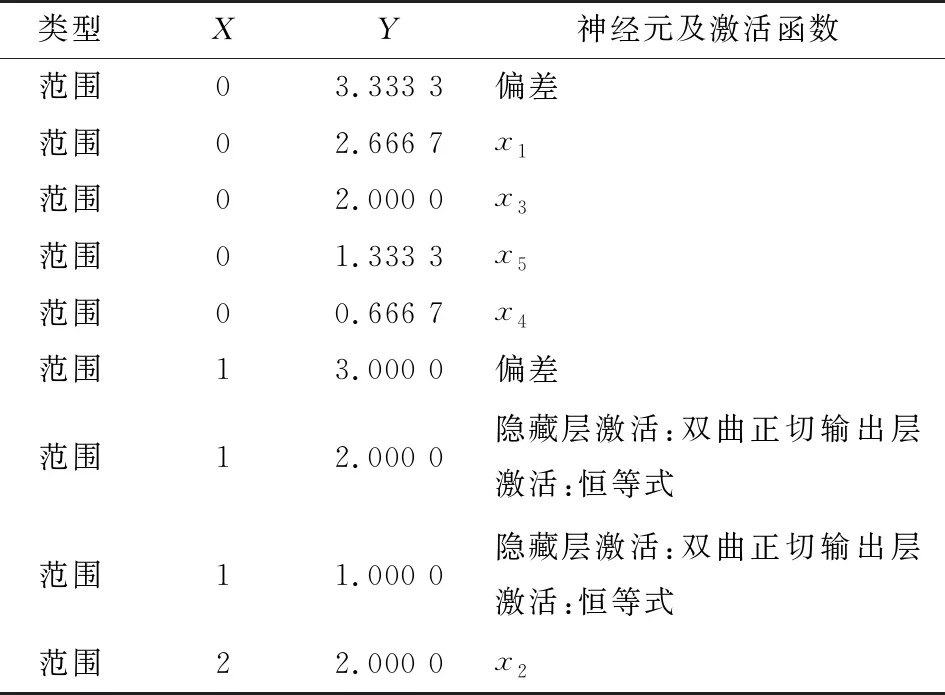
表5 松散回潮段神经网络结构信息

表6 各因子重要性

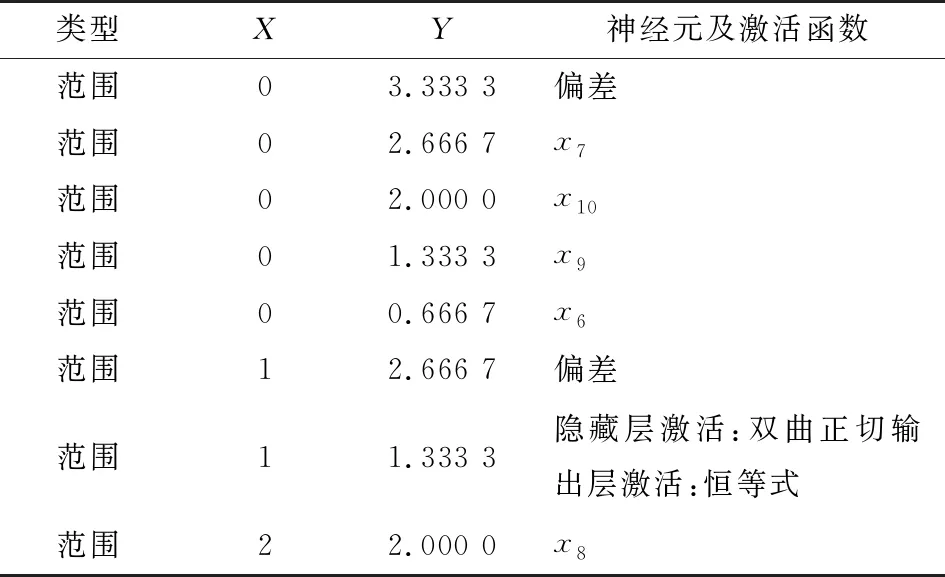
表7 加料回潮段神经网络结构信息

表8 各因子重要性

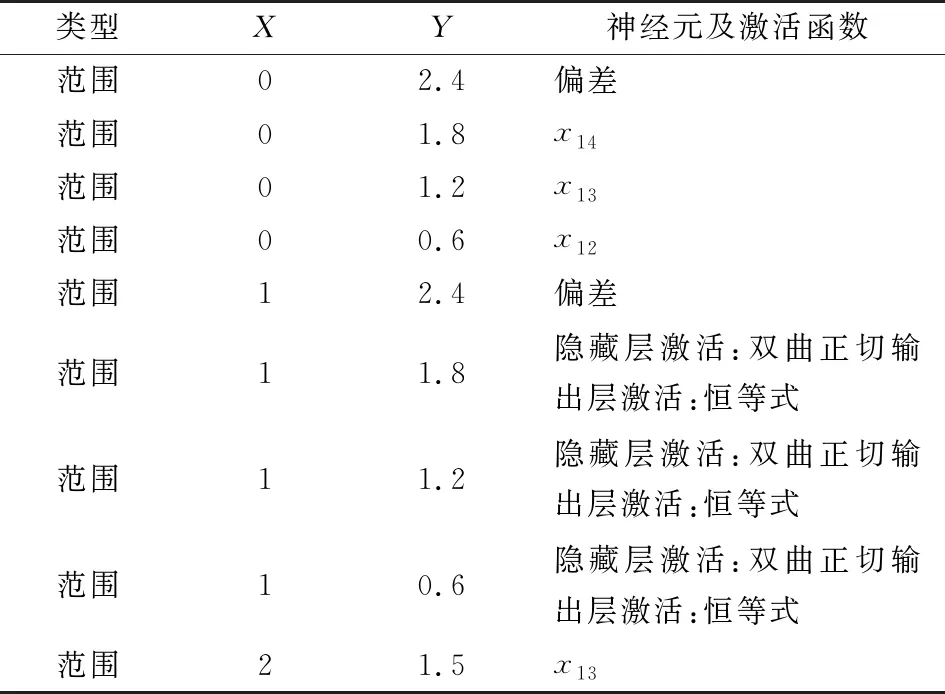
表9 热风润叶段神经网络结构信息

表10 各因子重要性

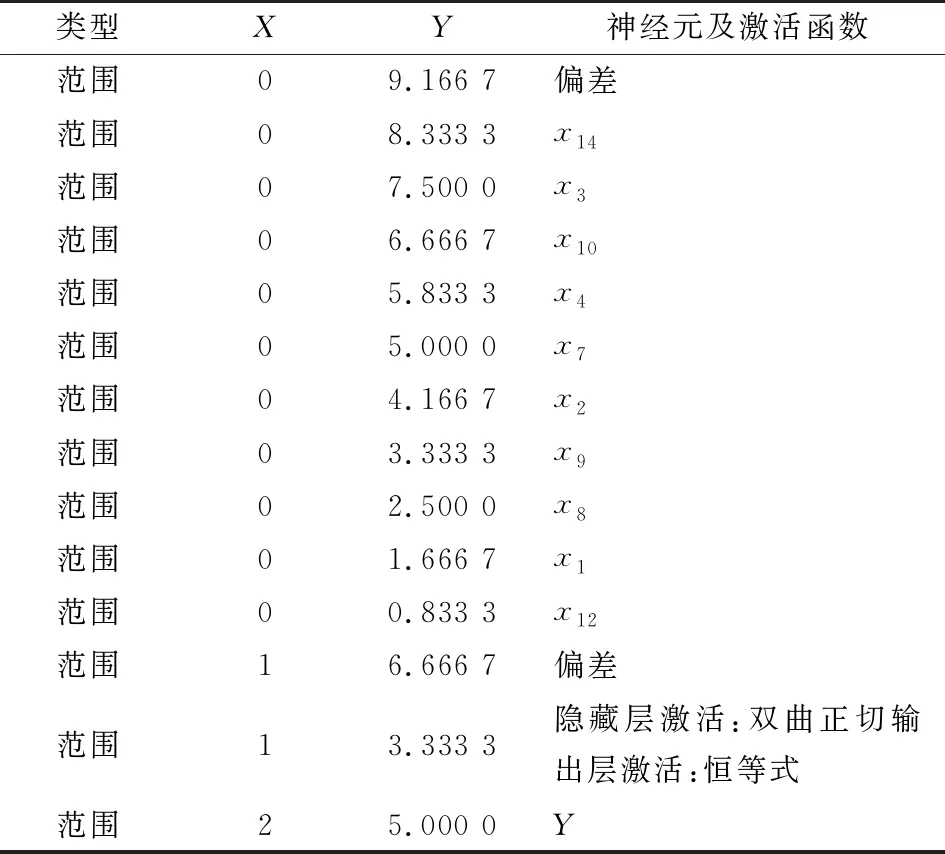
表11 烘丝入口水分神经网络结构信息

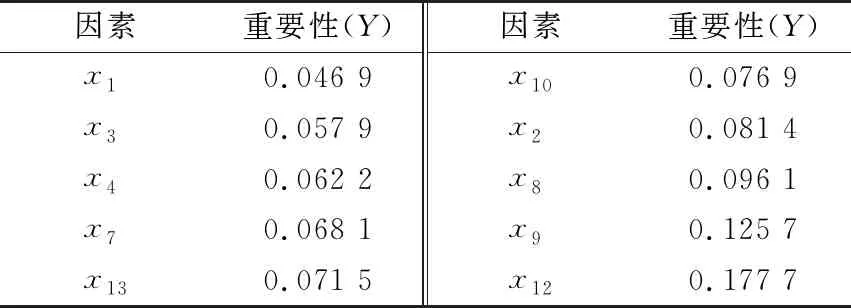
表12 各因子重要性

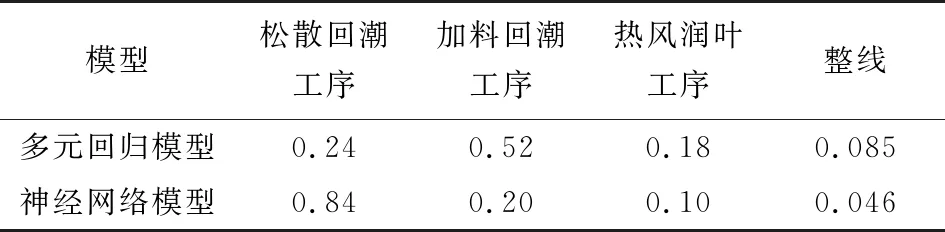
表13 工序模型预测精度统计

2.3 模型检验

2.3.1 试运行结果 采集2018年9月的生产数据进行试运行，其结果见表14。

由图2可知，模型预测与实际显示值之间趋势一致，且预测误差均<0.5。

2.3.2 数据验证 用T检验验证程序预估该阶段水分变化情况与实际情况是否一致，结果见表15、16。

由表16可知，各对组配对T检验中P值均大于0.05，二者差异不显著，即预测数据与实际数据一致，模型可靠。

3 模型应用

按各阶段含水率预测流程图3，利用C#语言编译，建立数据分析模块，应用SQLSERVER数据库存储数据，提供较稳定的数据传递速度，结合Three 3D插件，编译控件，通过对控件的操作，系统获取已知参数，自动进行数学模型分析，得出预测参数数值(图4)，形成预测系统。

4 结论

建模数据非线性情况下，使用神经网络方法建立预测模型的预测精度要高于多元回归法，反之，数据为线性的情况下，模型应选择多元回归法。松散回潮工序使用多元回归法建模，而加料回潮工序、热风润叶工序以及整线均采用神经网络法建模，利用各预测模型对生产过程数据进行预测，其误差分别为0.24%，0.20%，0.10%，0.046%，精度满足工艺要求，可被用于流水线智能化控制的前端分析模块。经研究系统预测精度还可以进一步提升，神经网络本身具备自学能力，能够自我提升预测准确度，因此，需不断收集数据，对模型进行不断训练，提升其预测精度。

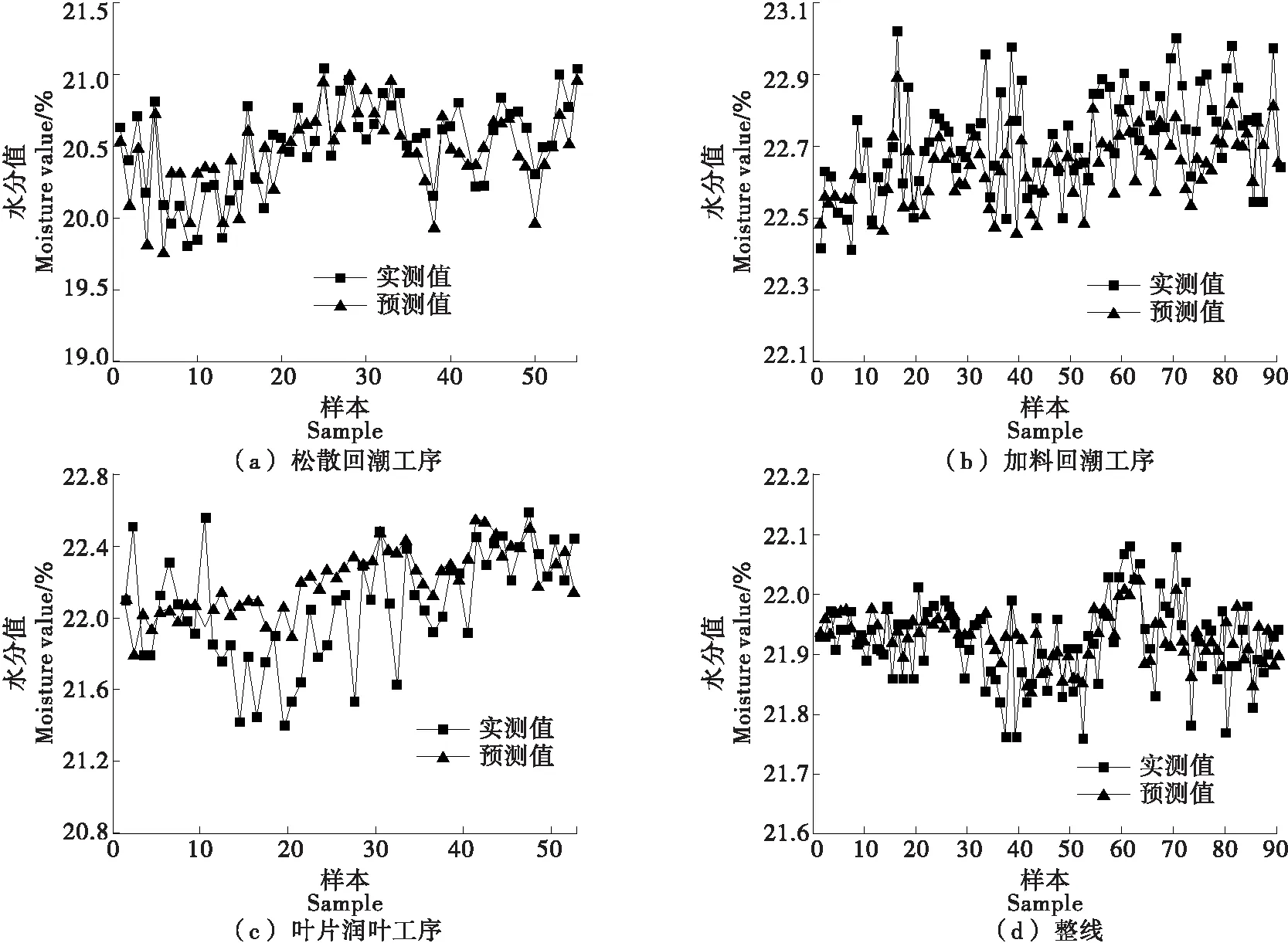
图2 预测值与实际显示值对比

表15 基本统计量

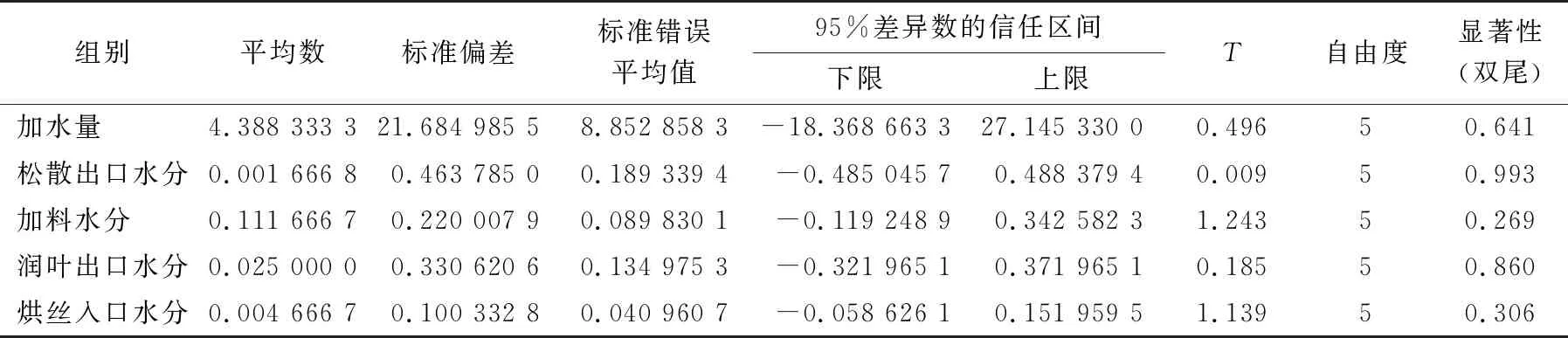
表16 预测值与实际值的配对T检验

图3 各阶段含水率预测流程

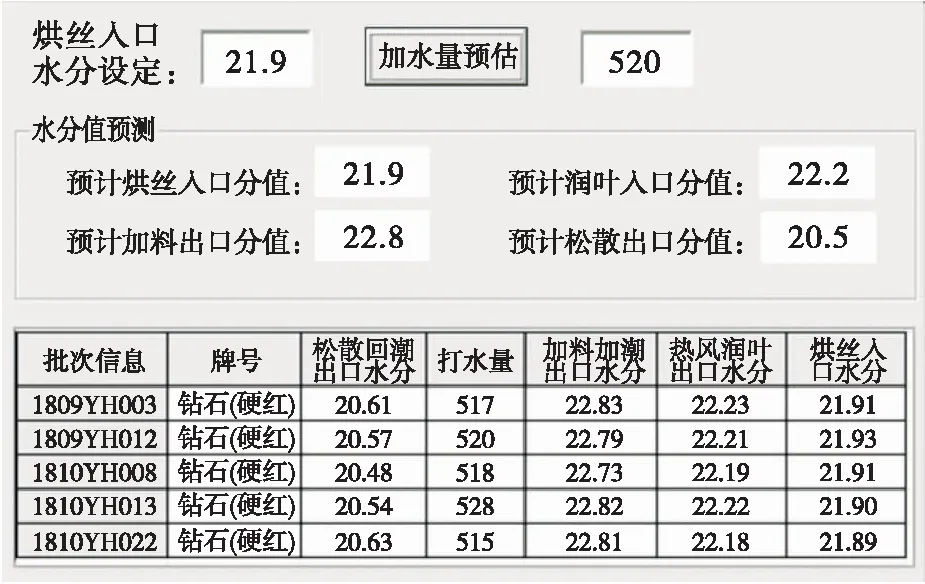
图4 预测系统示意图