基于FBG的复杂面形应变场检测系统研究

李莹莹，刘智超

(1.吉林工业职业技术学院 电气与信息技术学院,吉林 132013；2.长春理工大学 光电工程学院,长春 130013)

引 言

光纤布喇格光栅(fiber Bragg grating，FBG)传感器[1-3]是一种比较理想的无源传感与信号解调器件，应用于弯曲、位移、压力、应变、温度等多个参量的测量。光纤传感技术在航天、航海、石油化工、电力、生物医学等应用广泛[4-6]。针对复杂面形等进行检测时，由于受到自身重量、外界应力等因素产生应变而导致变形及偏移时，若不进行偏移量补偿，则导致基准测量不准，进而影响装配质量等问题。

目前，用于复杂面形的应变传感测量方法主要包括直接测量法[7]、电子测量方法[8]、光学测量法[9]和视觉测量法等[10]。直接测量法通过测量测量物体长度变化量从而测得应变大小，当物体或结构庞大或不易找到两个测量端时，该方法不可行[11]。电子测量方法是采用电阻应变片实现某一点的应变测量，这种测量方法虽然技术成熟、尺寸小、精度和灵敏度高，但不能进行3-D应变测量，容易受到电磁干扰，抗腐蚀能力弱[12]。激光扫描技术可实现非接触测量，测量范围和测量精度均可调，但该方法受CCD视场范围限制较大[13]。根据以上分析， FBG传感器[14-18]的优点在于抗电磁干扰、灵敏度高、尺寸小、重量轻、成本低, 适于在高温、腐蚀性等复杂环境中使用，在结构工程测量应变方面更有优势。本文中基于FBG传感网络的复杂面形应变场检测系统进行深入研究，实现复杂面形的基准位置、变形程度、变化趋势的定量测量，从而将应变场补偿量转化为位置精度修正量，得到校正模型以实现高精度数字化装配的应用。

1 系统设计

系统总体设计如图1所示。系统采用宽带光源为系统提供初始信号光，光通过光纤进入光纤耦合器，再进入FBG阵列段，分布在工件上的FBG阵列将各个测试点位上的应变物理量转化为FBG波长偏移量。FBG阵列分布满足在不同梯度上均匀排布的要求，图1中3条曲率变化不同的虚线表征梯度，将FBG阵列在3条特征梯度线上进行分布排列。这些回波再次通过光纤耦合器从而进入解调仪，由解调仪完成对回波光谱的解算，最终将各点位的数据转换成应变场分布数据。这些应变场分布数据可以根据不同的位置再验算成对应标准工件中3维坐标，在与标准数模中的坐标进行比较差分运算，从而获得数字装配校正数据。

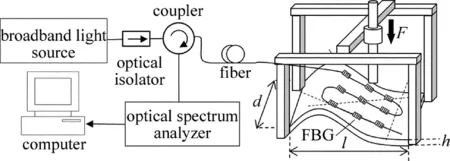
Fig.1 Complex surface shape strain field detection system

在工件受自身重力或外力产生形变的时候，工件表面会产生变形，从而导致FBG栅格受到影响，回波波长产生偏移，并且可以通过波长偏移量计算表面形变特性。设工件厚度为h，测试位置尺寸为l，变形量为Δl，当测试环境的温度恒定时，FBG探测点上的波长偏移与该点位上的应变符合(可由参考文献[19]中(2)式在温度补偿后化简得到)：

(1)

式中，λB为FBG的回波波长；ΔλB为FBG的回波波长偏移量；Pe为等效弹光系数。当黏贴在工件表面的FBG阵列跟随工件面形变化时，通过检测分析各个FBG位置的波长偏移量ΔλB，就能够完成各个位置应变量ε(即Δl/l)的计算。通过应变量变化完成对标准点3维坐标偏移量的计算，实现对工件标准点的校正。

设复杂面形待测件的数模标准点集合为U(x,y,z)，则当工件装配状态改变时，实际工件标准点集合为U′(x,y,z)。在工件装配过程中,为了保证状态改变产生的形变不造成装配超差现象，需要获得实际标准点集合与数模标准点集合的偏差集合ΔU(x,y,z)，该集合通过应变场测试数据反演得到，有:

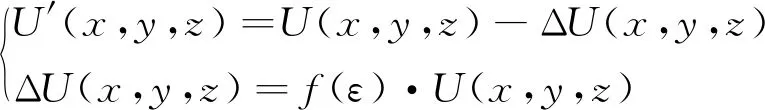
(2)

式中，f(ε)表示应变-坐标位置转换函数。最终，可以解算获得实际标准点的坐标为:

U′(x,y,z)=[1-f(ε)]·U(x,y,z)

(3)

2 仿真分析

采用SolidWorks软件对复杂曲面工件进行应变场及工件变形后微位移场模拟分析，仿真时板材材料选用601铝合金，厚度为5mm，密度为68.9kg/m3，泊松比为0.33。采用两段夹持、曲面区域不同位置施力的方法模拟，模拟施力范围50N～200N。将各点位上的FBG应变测试值解算后，再通过连续化插值的方法将有限点数据构建成结构曲面应变场分布，再结合工件材料特性，仿真结果如图2所示。

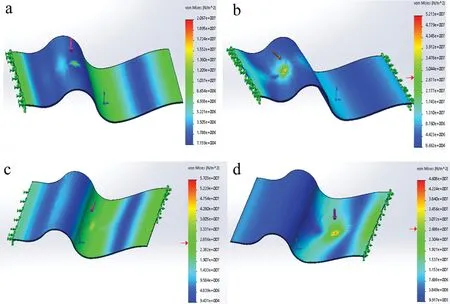
Fig.2 Simulation results of strain and displacement

对模拟工件进行应变场仿真，施力点分别在曲面顶点和底面，工件参量设置与实验拟测试工件一致，材质为合金铝，长20mm、宽10mm、厚5mm，(l×d×h)，表面呈不规律弯曲面形结构，外部施力F=200N。由图2a可知，当施力点在工件顶点时，顶面因受到外应力作用而产生变形，但变形程度不大，而其对应的下曲面段承受了主要作用力，其最大微位移变形量为0.301mm；由图2b可知，当施力点在工件顶点左侧时，应变范围明显大于顶点位置，但整体变形程度不大，其最大微位移变形量为0.426mm；由图2c可知，当施力点在工件顶点右侧时，左侧及顶面部分基本不变形，而右侧及底部曲面都发生了较明显的变形，其最大微位移变形量为0.512mm；由图2d可知，当施力点在工件底面时，底面因受到外应力作用而产生形变，形变分布以应变施力点为中心向外扩散，其最大微位移变形量为0.127mm，主要微位移区间在施力点附近。由此可见，不同应力施力点造成的微位移分布并不完全由施力点所决定，还会受工件结构所影响，故在FBG阵列分布设计时需要根据工件外形进行相应的分布调整。但整体趋势是应变场会根据施力点向支撑端延伸，垂直于支撑段的应变场衰减快，总体衰减趋势单调，但不同方向上衰减速率具有明显差异。

根据仿真分析结果可知，为了全面准确地反映待测工件的应变场分布，需要将FBG阵列尽可能地在不同梯度上均有一定排布，从而完整地获得整个工件面形应变场分布，更好地服务于数字化装配。以此设计思路，按照工件面形曲率变化程度设置了3条特征梯度线，并将FBG阵列在3条特征梯度线上进行分布排列。该排布设计可以最大程度反映不同梯度条件下的应变场分布，从而反映工件面形变化的真实状态。

3 实 验

3.1 实验条件

系统采用THORLABS公司的ASE宽带光源，1分2光纤耦合器，SOIL公司的BSIL-GS602型光纤光栅解调仪，表面黏贴型FBG传感探头。将FBG探头按照待测工件曲率分布梯度线均匀分布在待测表面上。工件的材质为合金铝，实验系统如图3所示。

Fig.3 Experimental device(1—demodulator,2—display,3—fiber,4—FBG,5—complex surface,6—test tooling,7—force arm,8—pre-ssure sensor,9—display for pressure,10—FBG for temperature compensated)

3.2 实验结果

将FBG阵列按照所设计的结构形式进行排布，每条梯度线上分布3个探头，以顶点右侧面载力的测试数据为例，9个探头的应变测试数据如表1所示。数据分析表中分别给出仿真分析值、应变测试验算值以及光学扫描测试值。

如表1所示，工件不同位置上对外加施力点的波长响应是不同的，其反映的微应变量也存在很大差异，故其微位移量也是根据不同位置而具有不同特性的。FBG序号从耦合器进入端开始顺序标识(No.1～No.9)。在以顶点右侧面载力条件下，斜线向下的曲率分布的3根FBG探头而言，5号波长偏移量最大，达到2.547nm，形成0.523mm的微位移，3号与7号亦有变化，但由此可见微位移改变量并不完全取决于距施力点的距离，与工件面形曲面位置也有关，该曲率梯度线上微位移量平均误差为0.012mm。底面曲率分布的3根FBG探头而言，6号波长偏移量最大，达到0.445nm，形成0.132mm的微位移，3号与9号变化基本一致，可见在平面条件下，应变场主要受到施力点与测试点距离的影响，该曲率梯度线上微位移量平均误差为0.009mm。直线向上的曲率分布的3根FBG探头而言，8号波长偏移量最大，达到1.643nm，形成0.347mm的微位移，7号与4号、1号应变量与位移量相近，可见曲面位置上对微位移量的影响主要由曲率决定。实验中测得最大波长偏移量为1.324nm,2.547nm和1.643nm，其分别对应的位移偏移量为0.244mm，0.523mm和0.347mm。将应变验算数据与光学精密测量数据对比可知，其相对误差均小于10%，应变数据可以有效反应结构形变。由实验数据可知，系统微位移量与应变FBG获取的波长偏移量具有函数关系，即可通过解调计算波长偏移量值实现对复杂面形应变场的检测。

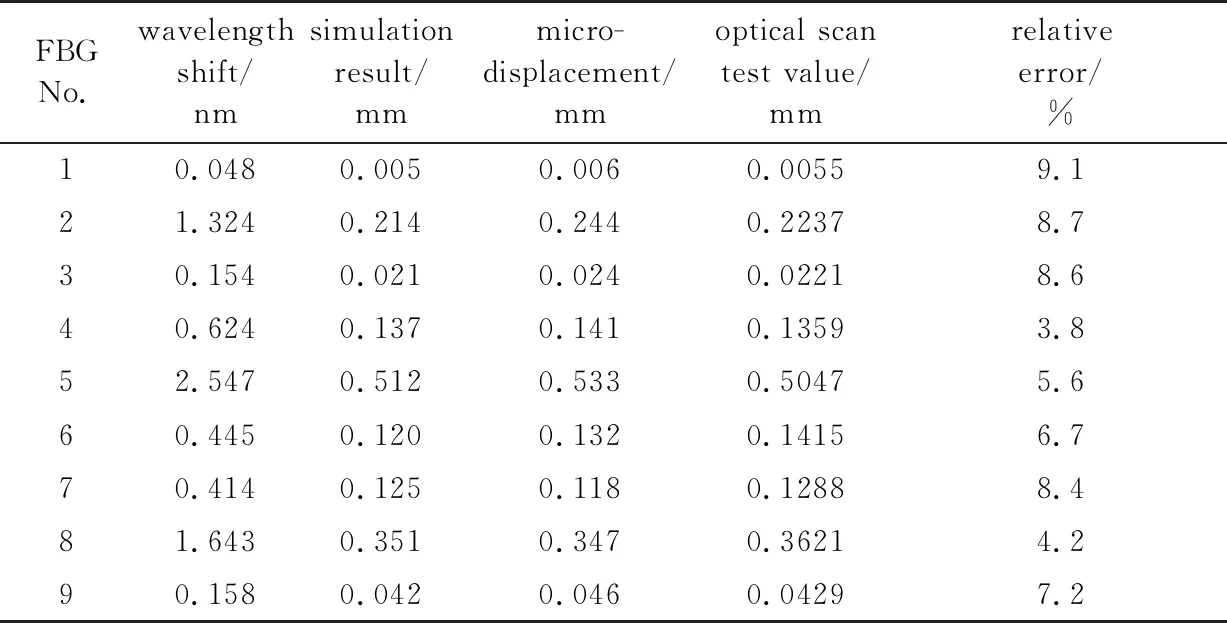
Table 1 Strain data of FBG

3.3 分析与讨论

根据FBG阵列获取的应变场分布测试数据可知，不同位置的外部施力会使工件产生变形，形变的量级受作用力大小、施力位置、曲面形态等所决定。根据波长偏移量与微位移量测试数据绘制的函数曲线如图4所示。

Fig.4 Displacement function of wavelength shift

在此基础上，对FBG阵列的位移偏移量测试数据与仿真数据进行误差分析，结果如图5所示。

Fig.5 Test error of different FBG

如图5可知，第1组FBG阵列(No.1～No.3)中位移偏移量平均误差是0.016nm，第2组FBG阵列(No.4～No.6)中位移偏移量平均误差是0.009nm，第3组FBG阵列(No.7～No.9)中位移偏移量平均误差是0.009nm。分析认为，包含拱面的测试数据误差相对较大，而平面部分的测试数据误差较小，系统总体平均误差符合要求。

4 结 论

本文中通过FBG传感阵列完成了对复杂面形工件的应变场及位移偏移量的测试。仿真计算了不同施力条件下待测件的应变分布和位移偏移量。实验验证了影响位移偏移量的主要参量，并给出了误差分布曲线。本系统对复杂面形工件的应变场及位移偏移量具有稳定的测试效果。