培数学之根，育素养之人

江苏省盱眙县第二中学 佟 利

数学核心素养是具有数学基本特征，适应个人终身发展和社会发展必须具备的关键能力与思维品质。数学课标修订组提出了六个核心素养：数学抽象、数学推理、数学建模、直观想象、数学运算、数据分析。我们如何培养学生的数学核心素养呢？笔者以“三角形中线性质”的学习为例来谈一谈自己的想法。

一、教学中注重培养学生直观与想象的能力

直观是学生通过观察认识图形、获取信息的过程，通过引导学生认真审题和观察图形，要做到心中有图。数学想象力也是数学学习中不可或缺的，要敢于大胆猜想。教师通过以下问题引导学生直观与猜想：如图1，AD 是△ABC 中BC 边上的中线，则中线AD 分得的△ABD 与△ACD 的面积有何关系呢？教师：图中有哪些三角形？请把它们表示出来。学生：△ABC、△ABD、△ABC。教师：猜想△ABC、△ABD、△ABC的面积有何关系？学生根据已有经验很容易得出它们之间的关系。通过直观找出相关三角形是研究三角形中线的前提，通过猜想得到命题，这是研究三角形中线性质的基础。

二、教学中注重引导学生证明与说理，培养学生科学严谨的态度

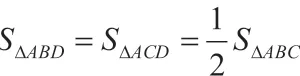
这只是知其然，我们还需要知其所以然。比如设问：“你能证明你得到的结论吗？”顺理成章地使学生走向证明的方向。总结归纳：三角形中线等分三角形的面积。

证明与说理使学生的思路更清晰，有助于培养逻辑推理能力，了解知识的来源，有利于培养学生严谨务实的数学态度。

三、在教学活动中积累基本活动经验，提高解决问题能力

我们已经得出了三角形的中线可以等分三角形面积的结论，下面要能运用真命题的结论解决问题，达到学以致用的目的。

活动1：有一块三角形的地，现要平均分给两个农户种植（即二等分三角形面积），请你想一想如何分，在图上作出分割线。

活动2：有一块三角形的地，现要平均分给四农户种植（即四等分三角形面积），请你想一想如何分，在图上作出分割线。

鼓励学生动手操作，把图画准确、画美观。学生归纳得出：先画中线完成二等分，再继续将分得的三角形二等分就可以完成四等分。在分割过程中获取了基本的活动经验，潜移默化地培养了学生的数学素养。

四、启发思考，引导数学建模，创造性解决问题

数学建模是对现实问题进行数学抽象，用数学语言表达问题，用数学知识与方法构建模型，从而解决问题的过程。

如图2，△ABC 的面积为a,延长△ABC 的边BC 到点D，延长边CA 到点E，使CD ＝BC，AE ＝CA，连接DE，则△DEC 的面积为______（用含a 的代数式表示），并说明理由。

学生通过已获得的经验，由中点联想到构造三角形中线数学模型。

甲同学思路：如图3，连接AD，由AC 是△ABD 边BD 上的中线，易得： ,再由AD 是△CDE 边CE 上的中线，易得：。

乙同学思路：如图4，连接BE，由AB 是△EBC 边CE 上的中线，易得： ，再由EC 是△EBD 边BD 上的中线，易得：。

两位同学的问题解决都是通过辅助线构造数学模型，完成了知识的转化，化未知为已知，化残为全。我们在整合题目条件时，练习所学数学模型，有则用之，缺则补之，无则化之，通过构造完整数学模型达成问题的解决。过程中教师应侧重学生数学抽象能力的培养，提供典型素材，供学生思维训练。在数学课程目标中，特别强调发展学生发现、提出问题与分析、解决问题的能力。

五、教学中鼓励学生敢于质疑，形成学习数学的批判精神

如图5，△ABC 的面积为1。第一次操作：分别延长AB，BC，CA 至点A1、B1、C1，使A1B=AB，B1C=BC，C1A=AC，顺次连接A1、B1、C1，得到△A1B1C1；第二次操作：分别延长A1B1，B1C1，C1A1至点A2、B2、C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2、B2、C2，得到△A2B2C2，……按此规律，要使得到的三角形的面积超过2020，最少要经过_次操作。

同学甲：根据上一题的模型我们可以得到： ，=6×6=36。设经过了n 次操作，只需要分析6n＞2020 中n 的最小整数值，得n=5。

乙同学：我认为甲的解法是错的。

老师：那你能说说你的见解吗？

老师：你说得真棒！

乙同学通过大胆质疑，指出甲的错误，并给出了自己的答案，这就是数学批判精神。在探究学习中，我们鼓励学生大胆运用结论，但有时也会出错。学习中我们允许有不同见解，但需要通过质疑、思维碰撞获取正确答案。质疑是一个优秀数学学者的必备素养，教学中需要鼓励大胆质疑，保护学生的科学批判精神。

在数学核心素养视角下，数学教育工作者要以全新的理念适应时代的教育，采用最有利于培养数学素养的方式，在课堂这块主阵地上播种数学核心素养的种子，让它生根、发芽并茁壮成长。每一个数学教育者都要砥砺前行，不忘初心，培养有终身学习能力的数学人才。