叶片进口边位置对快堆二回路钠泵空化性能的影响
杨从新, 余长虹, 于洪昌, 牛红军
(1. 兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省流体机械及系统重点实验室, 甘肃 兰州 730050; 3. 沈阳鼓风机集团核电公司, 辽宁 沈阳 110020)
快堆二回路钠泵(以下简称钠泵)是目前世界上最先进的第四代核电站冷却剂系统的核心装备,由于使用场合特殊,对其运行的安全性和水力性能的要求都非常高.主要过流部件有:直锥形吸入室、离心式叶轮、径向导叶、半球形压出室和进出口管路延伸段.分析核电站事故不难发现,冷却剂系统破坏是导致核电站事故发生的重要原因.空化影响离心泵运行的安全性和稳定性,因此钠泵性能的优劣,特别是空化性能,对四代核电系统的安全运行至关重要.近年来,许多学者研究了诱导轮长短叶片位置、诱导轮偏转角、叶轮进口几何参数等对离心泵空化性能的影响[1-4],以及叶片进口边位置对双吸离心泵、船用离心泵、深井离心泵水力性能的影响[5-7].但叶片进口边位置对核电站冷却剂泵水力性能及空化性能的影响鲜有报道.叶莉[8]研究了叶片进口边位置对小流量工况下离心泵空化性能的影响.何明辉等[9]研发了高效率低临界空化余量的离心泵.黄建德等[10]通过同时改变叶片进口边位置和叶片进口角,探究离心泵叶轮形状对汽蚀损伤的影响.离心泵的水力性能和空化性能具有耦合关系,由于钠泵使用场合特殊,在提升其空化性能的同时,还应保证尽可能小地牺牲水力性能.
本文针对快堆二回路钠泵的原型样机,保证叶轮其他几何参数不变,首先将叶片进口边前伸距离s1得到模型泵A,应用Fluent软件对模型泵A进行全三维定常单相及空化两相数值计算.判断叶片进口边前伸能否提升钠泵的空化性能,且水力性能的牺牲是否在可接受的范围内;如果结论是肯定的,通过调节叶片进口边前伸距离,探究使钠泵空化性能最优的叶片进口边位置,为核电站冷却剂系统离心泵叶轮设计和性能优化提供借鉴资料.
1 计算模型与数值计算方法
1.1 模型建立
快堆二回路钠泵原型样机以水为输送介质的主要设计参数为:设计流量qV,d= 630 m3/h,扬程Hd=35 m,效率ηd=81%,比转速ns=105,许用汽蚀余量为4 m,转速n=990 r/min,功率P=70.37 kW,叶轮叶片数Z1=6,导叶叶片数Z2=10,泄漏量q=60 m3/h.图1为钠泵原型样机的三维水体图.
针对原型样机,参考文献[11]及常规离心泵空化性能的提升方法,设计通过前伸叶片进口边提升钠泵空化性能的流程,如图2所示.流程图中左半部分为叶片进口边前伸能否提升钠泵空化性能的验证,若计算结果表明模型泵A的水力性能变化量超出了钠泵正常运行的范围,或空化性能未提升,放弃通过前伸叶片进口边提升钠泵空化性能的方法;否则进入右半部分(虚线圈起来的)钠泵空化性能最优的叶片前伸距离探究循环流程.流程图中i≥2,记模型泵i为模型泵B(i=2),依次类推.为保证进出口段流动均匀,避免边界条件对数值计算结果的影响,将原型样机、模型泵A和模型泵i的进出口段分别进行4倍管径延伸.叶片进口边前伸时,保证叶轮其他几何参数不变,且叶片型线基本保持不变;从叶片进口边按下式所示的等差数列,增大叶片包角φ,且从叶轮前盖板到后盖板按相同的角度增大叶片包角:
φ=φ0+(n-1)d
(1)
式中:φ0为原型样机包角;公差d= 2°.
图3是探究钠泵空化性能最优的叶片进口边位置过程中,各模型泵与原型样机叶轮在子午面上的投影.模型泵A、B、C的叶片进口边在原型样机叶片进口边基础上前伸距离分别为s1、s2、s3(曲线距离),其值见表1.原型样机及模型泵A、B、C的叶片进口角,从后盖板侧到前盖板侧变化如图4所示.
1.2 数值模型
基于Fluent软件对原型样机和各模型泵分别进行全三维定常单相数值计算,假设未发生空化的流场不可压缩,选用RNGk-ε湍流模型封闭方程组,压力和速度耦合采用SIMPLE算法.动量方程、湍动能与耗散率输运方程均采用一阶迎风格式,各收敛精度取10-6.对原型样机进、出口压力和进口速度进行监测,监测值变化趋于稳定,且变化量小于5%时认为计算收敛.
为了更准确地预测不同工况下各模型泵的空化性能,以原型样机单相计算收敛的结果为初值,应用目前对离心泵空化性能预测较准确的Zwart-Gerber-Belamri和Schnerr&Sauer空化模型[12-13],分别对原型样机不同工况下的空化性能进行全三维定常数值模拟,空化两相数值计算考虑空化流的压缩性.压力和速度耦合采用Quick算法,动量方程采用Pesto算法离散,能量方程、湍动能方程、体积分数方程与耗散率方程均采用一阶迎风格式,取各收敛精度为10-6,将空泡体积分数加入监测项.
选择不同工况下对钠泵原型样机空化性能预测更准确的空化模型,对各模型泵对应工况的空化性能进行全三维定常数值模拟.
旋转区域和静止区域之间的耦合采用多重参考系模型,进口采用压力入口边界条件;出口采用速度出口边界条件,假定出流速度均匀分布,方向垂直于钠泵出口截面,给定出流速度大小;壁面函数采用对y+适应范围更广的加强壁面函数[14-15].
2 网格划分与试验验证
2.1 网格划分
钠泵的叶片是复杂的三维扭曲叶片,故计算域采用适应性较好的非结构化网格,对流场参数变化梯度大的区域进行局部网格加密,壁面加棱柱边界层网格,尽可能保证y+=30~300,即壁面第一层网格节点分布在对数律层.原型样机计算域网格如图5所示.
为了得到保证计算结果的最小网格数,对原型样机进行网格无关性验证,如图6所示.由图中可以看出,网格数约1 050万后,网格数继续增大,扬程的变化在0.5%以内,因此原型样机计算域网格数取10 625 343.
采用原型样机最终确定的网格尺度,按原型样机的网格划分方法,对模型泵A、B、C的叶轮进行非结构化网格划分,其他过流部件采用原型样机的网格.模型泵叶轮网格数和总网格数如图7所示.
2.2 试验验证
为了验证数值计算的准确性,将计算值与试验结果进行对比.图8为原型样机的扬程、效率、轴功率计算值与试验结果的对比,由图中可以看出,计算值与试验结果吻合较好,扬程最大误差为5.54%,效率最大误差为3.13%,轴功率最大误差为2.37%,误差均在可接受的范围内,因此文中采用的数值计算方法是可靠的.
2.3 不同工况下空化模型验证
图9为不同工况下,两种空化模型对原型样机空化性能的计算值与试验结果对比.由图中可以看出,0.8qV,d~1.1qV,d工况,Schnerr&Sauer空化模型对钠泵临界空化余量计算值更接近试验值,其他工况,Zwart-Gerber-Belamri空化模型对钠泵临界空化余量计算值更接近试验值.
3 计算结果与分析
3.1 叶片进口边前伸对钠泵水力性能的影响
图10为各模型泵与原型样机扬程、效率、轴功率的计算值对比,表2为不同工况下各模型泵扬程与原型样机扬程的差值.
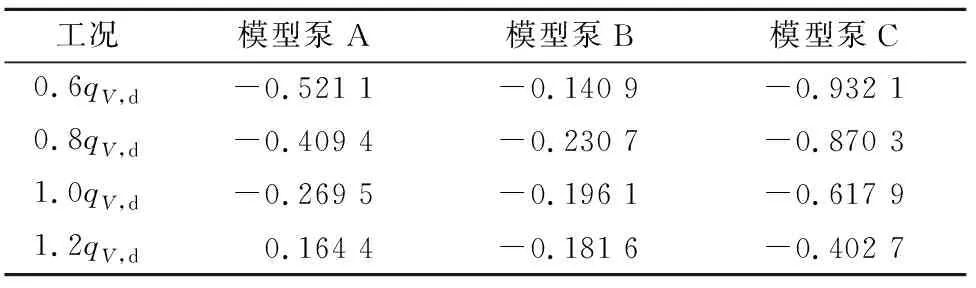
表2 不同工况下各模型泵扬程变化Tab.2 Head change of each model pump under different flow rate conditions m
由图10可以看出,随着流量的增大,各模型泵与原型样机的扬程、效率、轴功率变化趋势基本一致.与原型样机相比,模型泵A在小流量工况扬程下降明显;设计工况和大流量工况,扬程几乎无变化,最大降低量为0.521 1 m.模型泵B扬程下降最少,最大降低量为0.231 0 m.模型泵C的扬程明显降低,最大降低量为1.182 0 m.各模型泵在设计工况下,扬程变化量最小.
从效率曲线可以看出,模型泵A的效率下降最明显,最大降低量为2.32%;模型泵B在小流量工况效率略高于模型泵A,设计工况和大流量工况与模型泵A基本一致,模型泵B效率最大降低量为1.50%;模型泵C小流量工况效率与原型样机基本相同,设计工况和大流量工况效率低于原型样机的效率,效率最大降低量为1.68%.
从轴功率曲线可以看出,在设计工况下,模型泵的轴功率小于原型样机的轴功率,其他工况与原型样机基本相同.
叶片进口边前伸使流体提前接触到叶片,同时减小了叶轮进口部分的排挤系数,各模型泵扬程和效率变化是两者共同作用的结果.利用加权方法,将多目标问题转化为单目标问题求解.由上述计算可知,叶轮进口边不同程度前伸对钠泵轴功率几乎没有影响,因此,分别对扬程和效率赋予权重k1、k2,定义评价函数为:K=k1H+k2η.考虑到扬程与效率权重比例,取k1=k2=0.5,k1+k2=1,表3为模型泵性能指标.
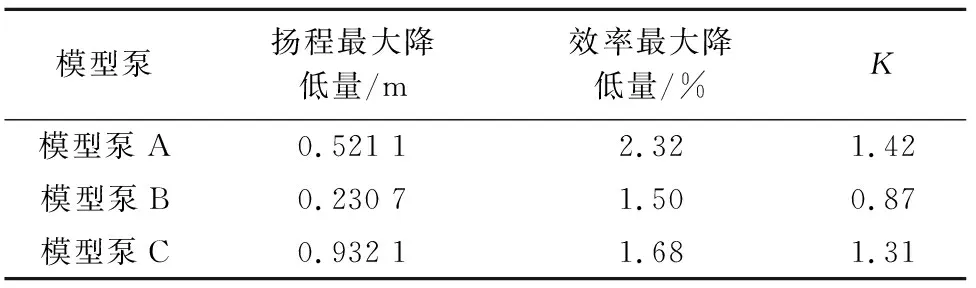
表3 模型泵性能指标Tab.3 Performance index of model pump
K值越大,表明模型泵外特性下降越多,由表3可知外特性降低量:模型泵B<模型泵C<模型泵A.
3.2 叶片进口边前伸对不同工况下钠泵空化性能的影响
引入有效空化余量:
(2)
式中:ρ为流体密度,kg/m3;g为当地重力加速度,m/s2;vs为泵进口处的速度,m/s;pv为流体在当地环境下的汽化压力,Pa.
空化数值计算模仿空化试验,即不断降低钠泵进口压力ps,探究扬程的变化情况.图11为不同工况下各模型泵与原型样机空化性能对比.
图11a为0.6qV,d工况下,基于Zwart-Gerber-Belamri空化模型,各模型泵与原型样机空化性能对比.由图中可以看出,随着有效空化余量的降低,各模型泵扬程与原型样机扬程变化趋势基本相同,扬程突降前,模型泵A与原型样机的扬程差值最大,最大差值为0.78 m;模型泵B与原型样机的扬程差值小于模型泵A,与原型样机的最大差值为0.67 m;模型泵C与原型样机的扬程差值最小,最大差值为0.26 m.扬程突降时的有效空化余量:模型泵B<模型泵C<模型泵A<原型样机.
图11b为0.8qV,d工况下,基于Schnerr& Sauer空化模型,各模型泵与原型样机空化性能对比.由图中可以看出,随着有效空化余量的降低,扬程均呈现先上升后下降,随后急剧下降的趋势.有效空化余量小于约4 m后,模型泵A比原型样机扬程有所增大,模型泵B比模型泵A扬程增大量更多,模型泵C的扬程比原型样机扬程低.扬程突降时的有效空化余量:模型泵B<模型泵A<模型泵C<原型样机.
图11c为设计工况下,基于Schnerr& Sauer空化模型,各模型泵与原型样机空化性能对比.可以看出:扬程突降前,各模型泵的扬程大于原型样机的扬程;有效空化余量约大于6 m时,模型泵A的扬程大于模型泵B的扬程,之后模型泵B的扬程大于模型泵A的扬程,模型泵C的扬程呈现波浪式变化趋势,说明模型泵C运行不稳定.扬程突降时的有效空化余量:模型泵C<模型泵B<模型泵A<原型样机.
图11d为1.2qV,d工况下,基于Zwart-Gerber-Belamri空化模型,各模型泵与原型样机空化性能对比.由图中可以看出,扬程突降前,各模型泵的扬程小于原型样机的扬程,且各模型泵的扬程基本相等.与原型样机相比,各模型泵扬程突降时的有效空余量均不同程度减小,具体为:模型泵A<模型泵B<模型泵C.原因是大流量工况对叶轮过流能力的要求更高,叶片进口边前伸减小了叶轮进口的排挤系数,过流能力减弱导致能量损耗增多,使钠泵提前发生空化.
3.3 各模型泵空化特性验证
文献[11]规定,泵扬程下降3%时的有效空化余量为临界空化余量.通过上述空化数值计算得到不同工况下各模型泵的临界空化余量,图12为各模型泵临界空化余量对比图.由图中可以看出,叶片进口边不同程度前伸,降低了不同工况下钠泵的临界空化余量.随着流量的增大,临界空化余量:原型样机逐渐增大,模型泵A和模型泵B先减小后增大,模型泵C先增大后略微减小,再增大.小流量工况和大流量工况模型泵B的空化性能最优,设计工况模型泵C的空化性能最优.由图12可知,模型泵C在设计工况下运行的稳定性受到影响,为了保证钠泵运行的稳定性,设计工况选择空化性能略低的模型泵B .
综上所述,叶轮进口边不同程度前伸,钠泵的水力性能均有不同程度下降,下降量:模型泵B<模型泵A<模型泵C<原型样机.钠泵空化性能:模型泵B>模型泵C>模型泵A>原型样机.因此,模型泵B既保证了钠泵水力性能较小的下降量,同时提升了钠泵的空化性能.
3.4 叶片进口边前伸对钠泵内流场的影响
由文献[11]可知,离心泵空化一般发生在叶轮内.因此,对设计工况下不同有效空化余量时各模型泵叶轮内的空泡体积分数进行对比,从而判断叶片进口边不同程度前伸提升钠泵空化性能的阶段,如图13所示.
由图13可以看出,有效空化余量为6.53 m时,叶片背面进口边有少量空泡分布,叶轮内空泡体积分数:原型样机>模型泵A>模型泵B>模型泵C,即叶片进口边位置前伸的越多,空泡体积分数越小.叶片进口边前伸,使流体提前接触到叶片,流体能量得到了补充,减弱了钠泵的空化程度.
有效空化余量为4.49 m时,叶片背面空泡分布范围进一步扩大;模型泵A与原型样机的空泡分布范围基本一致,但空泡体积分数明显小于原型样机空泡体积分数.空泡体积分数:原型样机>模型泵A>模型泵B>模型泵C.
有效空化余量为0.92 m时,叶片背面有大量空泡分布,叶片工作面靠近叶轮前盖板侧空泡聚集程度较明显.空泡体积分数:模型泵C>模型泵A>原型样机>模型泵B.
通过对比不同有效空化余量时各模型泵叶轮内的空泡体积分数,可以得到如下结论:叶轮进口边位置不同程度前伸,减弱了不同有效空化余量时钠泵的空化程度;完全空化时,空泡充满流道阻塞流体流动,叶片进口边前伸减小了排挤系数,对空化流的阻塞作用更明显.
4 结论
1) 叶片进口边前伸使流体提前接触到叶片,同时减小了叶轮进口的排挤系数,从计算结果可以看出,叶片进口边前伸对流体排挤造成的能量损失比叶片提前提供给流体的能量多.整体看来,叶片进口边前伸对钠泵水力性能的影响不大,其中模型泵B的水力性能下降量最小.
2) 叶片进口边前伸减小了钠泵的临界空化余量,扩大了钠泵的安全运行范围,前伸距离越大,钠泵的空化性能提升越多,但叶片进口边前伸距离过大,随有效空化余量降低扬程出现波动现象,即影响钠泵运行的稳定性,因此模型泵B空化性能最优.
3) 叶片进口边前伸使叶片背面进口边压力最低点的压力增大,减弱了钠泵的空化程度.
综上所述,模型泵B在保证水力性能下降量最小,且不影响钠泵稳定运行的情况下,空化性能最优.

