基于在线相位角辨识的改进落点预测修正算法

霍鹏飞，雷泷杰，施坤林

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

二维弹道修正引信是在保留引信原有功能的基础上，增加二维弹道修正功能的新型引信，具有命中精度高、成本低等优点，能对传统弹药进行精确化打击改造，是弹药实现低成本精确打击的重要途径。155 mm炮弹二维弹道修正引信是国际上研究的热点。目前国际上该平台的二维弹道修正引信可分为三类：一类是制导系统在引信中的集成，如美国GIF、以色列TopGun、南非的C2、德国的2DCCF，旨在实现圆概率误差(CEP)小于10 m；一类是基于翼面减旋、固定翼舵机的二维修正引信，如美国的PGK，旨在实现CEP小于50 m；另一类是基于引信整体减旋、可动翼舵机的二维修正引信，如英国BAE银弹引信，旨在实现CEP小于20 m[1]。无论是哪一类方案，修正控制算法均是整个系统的核心技术。修正算法是通过实际测量得到的弹丸位置信息，结合目标位置，根据导引规律形成修正指令。滚转角控制模块进一步实现引信滚转稳定，最终导引弹丸飞向目标。就修正算法而言，导弹等大机动智能弹药机动能力强，能够实现比例导引算法过载指令要求，应用成熟的传统比例导引算法便可以实现对目标的高精度打击[2]。而二维弹道修正引信机动性小，无法实现比例导引算法实时过载要求，目前使用较多的是基于落点预测的修正算法[3]。

基于落点预测的修正算法目前主要有经典落点预测修正算法、基于离线相位角的改进落点预测修正算法以及基于比例因子的改进落点预测修正算法[4]。其中经典落点预测修正算法适用于微旋或者非旋转弹，对于高旋弹而言，由于旋转引起的弹丸气动不对称性导致修正指令相位角偏移[5]，经典落点预测修正算法未对该偏移量进行修正，难以确保弹丸击中目标[6]。这就衍生出了基于离线相位角的改进落点预测修正算法以及基于比例因子的改进落点预测修正算法[7]，这两种方法均对旋转引起的弹丸气动不对称性导致修正指令相位角偏移进行了补偿，但是均是采用离线处理的方法对补偿项进行估计，而弹丸在实际飞行过程中受到气象、射击等条件的影响，修正指令相位角偏移量会发生变化，该变化也会直接影响弹丸命中精度[8]。针对目前弹丸在实际飞行过程中，二维弹道修正引信修正指令离线补偿存在相位角偏移量估计误差问题，提出了基于在线相位角辨识的改进落点预测修正算法。

1 落点预测修正算法

1.1 经典落点预测修正算法

经典落点预测修正算法的原理是在每一个修正时刻到来时，首先根据弹丸数学模型预测出弹丸落点坐标(xp，yp，zp)，结合预先设定的目标位置坐标(xt，yt，zt)计算出弹丸预测落点相对于目标的纵向位置偏差ex和横向位置偏差ez，修正算法根据横纵向位置偏差计算出修正指令φid。控制系统控制引信跟踪修正指令φid，修正弹丸落点至目标位置。下一修正时刻到达时，重复上述过程，对弹丸飞行弹道不断修正，导引弹丸飞向目标。对于二维弹道修正引信而言，其修正指令为引信滚转角控制指令。经典落点预测修正算法修正指令计算过程如下：

(1)

(2)

1.2 改进落点预测修正算法

改进的落点预测算法是在经典预测算法的基础上发展起来的，对于二维弹道修正引信而言，其往往被用来对无控高速旋转弹或低速旋转弹进行精确化打击改造。在高速或低速旋转弹平台，经典落点预测修正算法解算得到的修正指令与其实际所能够产生的修正方向之间存在一定相位角偏差，弹丸在实际飞行过程中受到气象、射击等条件的影响，该相位角偏差会不断变化。改进的落点预测算法通常可以表示为式(3)所示表达式，其中K(t)代表t时刻的比例修正因子，φb(t)代表t时刻的修正指令相位角补偿项。

(3)

基于相位角的改进落点预测修正算法是在经典落点预测修正算法修正指令的基础上增加固定的相位角补偿项，实现对修正指令相位角偏差的补偿。基于比例因子的改进落点预测修正算法是通过引入仿真计算拟合得到的体现横纵向修正能力的比例修正因子的方式实现对修正指令相位角偏差的补偿。

2 基于在线相位角辨识的改进落点预测修正算法

由于弹丸在实际飞行过程中基于相位角的改进落点预测修正算法采用的固定相位角补偿项以及基于比例因子的改进落点预测修正算法对修正指令相位角偏差的补偿这两种离线补偿方式均存在偏差，基于在线相位角辨识的落点预测修正算法采用了在线补偿的方式，流程如图1所示。

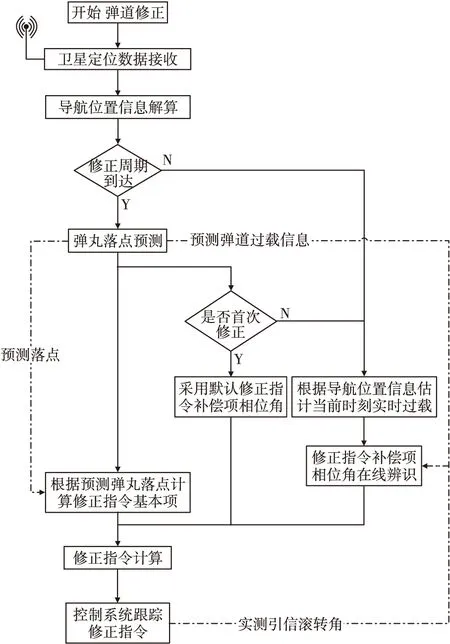
图1 基于在线相位角辨识的落点预测修正算法流程Fig.1 The flow chart of improved placement prediction algorithm based on online phase angle identification

基于在线相位角辨识的改进落点预测修正算法具体步骤如下：

1)弹道修正模块开始启动后，卫星定位模块输出卫星定位数据，导航模块根据卫星定位数据解算弹丸位置信息，包括发射坐标系弹丸位置坐标(x,y,z)以及弹丸速度矢量(Vx，Vy，Vz)。

2) 当修正模块启动后，修正周期到达时，落点预测模块根据步骤1)中得到的当前时刻弹丸位置、速度信息对弹丸剩余飞行弹道进行预测，记录每一时刻弹丸飞行弹道过载信息，设记录时间间隔为Δt，起始时刻为当前弹丸已飞行时间t0，时间序列记为T，至落地时刻，总数为N，可以表示为式(4)表达式。弹丸飞行弹道过载信息可以用三个数组表示Nx,Ny,Nz，如式(5)表达式所示，直至预测至弹丸落地。若修正模块启动后，修正周期未到达时，直接采用当前存储的上一次落点预测结果，转入下一步修正指令相位角计算。

T=(t0,t1,…,tn,…,tN)n=1,2,…,N

(4)

n=1,2,…,N

(5)

预测弹丸落地时，存储弹丸预测落点坐标(xp,yp,zp)，以及整个飞行过程弹丸过载信息，过载序列按照二维线性数据表存储，Table[TNx],Table[TNy],Table[TNz]。

根据预测得到的落点坐标与发射前装定的目标位置坐标(xt,yt,zt)，采用式(6)和式(7)更新修正指令基本项φ0。

(6)

(7)

3) 若为首次修正，则采用默认修正指令补偿相位角φb0，默认修正指令补偿项相位角通过发射前配置。若非首次修正，对修正指令相位角补偿相进行在线辨识。设上一次卫星定位数据更新时刻弹丸速度矢量为(Vxp,Vyp,Vzp)，根据式(8)结合步骤1)得到的导航位置信息估计当前时刻实时过载(Nxi,Nyi,Nzi)，设Ts为卫星定位数据更新周期。

(8)

根据当前时刻时间ti，分别对落点预测结束后存储的过载序列表Table[TNx],Table[TNy],Table[TNz]进行拉格朗日插值，得到预测弹道此时弹丸过载信息(Nxi0,Nyi0,Nzi0)，通过计算当前过载估计值与预测弹道理论解算值之间误差(Nxie,Nyie,Nzie)，结合实际测量得到的修正翼面滚转角γi，利用式(9)求解出当前修正相位角φei，在此基础上，利用式(10)辨识出当前时刻修正指令补偿项相位角φbi。

(9)

φbi=φei-γi

(10)

根据得到的修正指令基本项和修正指令补偿项相位角，采用式(11)计算修正指令φi。控制系统控制引信滚转角γ，实现对修正指令φi跟踪。

φi=φ0+φbi

(11)

重复步骤1)至步骤3)，直至弹丸落地。

3 仿真验证

为了验证基于在线相位角辨识的改进落点预测修正算法的可行性，在155 mm杀爆弹平台对该算法进行了六自由度外弹道仿真。完成对该算法可行性的仿真验证后，进一步对采用该算法进行弹道修正与采用基于离线相位角的改进落点预测修正算法和基于比例因子的改进落点预测修正算法进行弹道修正时的目标打击CEP进行蒙特卡洛仿真，通过对比采用不同算法仿真得到的相位角估计偏移误差以及CEP大小评价不同算法的优劣。相位角估计偏移误差和CEP越小，说明对应算法更具备优势。

首先对基于在线相位角辨识的改进落点预测修正算法的可行性进行验证，初速采用名义值930 m/s，射角51°，选用海拔1 380 m处实测气象。仿真得到无控弹落点发射坐标系落点坐标为X=32 444 m，Y=0 m，Z=1 333 m，根据155 mm杀爆弹无控弹散布特征，选择最大修正量2%，目标点设定为Xm=32 000 m，Zm=1 000 m，t=30 s时刻开始弹道修正，仿真得到的弹丸飞行弹道如图2所示，30 s开始修正后修正指令补偿项相位角变化如图3所示，二维弹道修正引信滚转角变化曲线如图4所示。

图2 基于在线相位角辨识的落点预测修正弹丸飞行弹道Fig.2 Trajectory of projectile corrected by prediction of impact point based on on-line phase angle

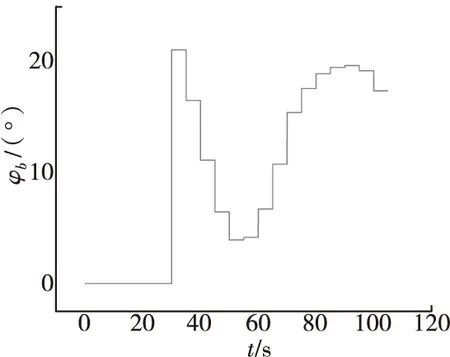
图3 修正指令补偿项相位角变化曲线Fig.3 The change curve of compensation phase angle as modified command

图4 二维弹道修正引信滚转角变化曲线Fig.4 Roll angle curve of two dimensional trajectory correction fuze

为了得到对比采用不同算法仿真得到的相位角估计偏移误差以及CEP大小，引入表1所列误差项，对弹丸修正精度进行200次蒙特卡洛仿真，采用基于在线相位角辨识的改进落点预测修正算法可行性验证相同仿真条件，对基于相位角的改进落点预测修正算法以及基于比例因子的改进落点预测修正算法精度进行了仿真验证，采用不同修正算法时仿真得到的修正段相位角偏移量估计误差统计特性以及弹丸对目标打击精度CEP大小如表1所示。采用基于在线相位角辨识的改进落点预测修正算法仿真得到的弹丸落点散布如图5所示。

图5 采用基于在线相位角辨识的改进落点预测修正算法蒙特卡洛仿真结果Fig.5 Monte Carlo simulation results of improved impact point prediction algorithm based on online phase angle

表1 修正弹丸精度仿真误差Tab.1 Accuracy simulation error of corrected projectile

从表2仿真结果对比可以看出：采用不同修正算法仿真得到的相位角偏移量估计误差中，基于在线相位角辨识的改进落点预测修正算法仿真得到的相位角偏移量估计误差为0°，其他两种算法仿真得到的相位角偏移量估计误差均大于5°；同时基于在线相位角辨识的改进落点预测修正算法仿真得到的CEP为22.2 m，较其他两种算法仿真得到的CEP提升25%以上。证明基于在线相位角辨识的改进落点预测修正算法能够有效补偿弹丸飞行过程中由于射击、气象等条件扰动所带来的对修正指令相位角偏移量的影响，克服修正指令离线补偿存在相位角偏移量估计误差问题，提升弹丸对目标打击精度。

表2 不同修正算法仿真得到的相位角偏移量估计误差及目标打击精度CEP对比Tab.2 Comparison of phase angle offset estimation error and target strike accuracy CEP obtained by different correction algorithms

4 结论

本文提出了基于在线相位角辨识的改进落点预测修正算法，该算法采用导航位置信息估计当前时刻实时过载，根据当前时刻时间，对落点预测弹道存储的预测弹道过载信息进行插值，得到预测弹道此时弹丸过载信息，通过计算当前过载估计值与预测弹道理论解算值之间误差，结合实际测量得到的修正翼面滚转角信息，对修正指令补偿项相位角进行在线辨识。仿真结果表明，基于在线相位角辨识的改进落点预测修正算法能够根据弹丸实际飞行状态在线估计出修正指令相位角偏移量，与离线补偿算法相比，能够有效补偿弹丸飞行过程中由于射击、气象等条件扰动所带来的对修正指令相位角偏移量的影响，克服修正指令离线补偿存在相位角偏移量估计误差问题，弹丸对目标打击CEP提升至少25%。同时该算法实现简单，具有较好的工程可实现性。