基于径向基函数的自适应网格方法

段献葆， 党 妍， 秦 玲

(西安理工大学理学院，西安 710048)

1 引言

许多物理和工程实际问题都可以用偏微分方程来描述，但是只有极少数的偏微分方程可以得到精确解，所以对于一般的偏微分方程，都是借助于数值方法求解.比较成熟的数值方法中大部分是依赖于网格的，如有限差分法、有限元法、有限体积等等.这些方法必须先生成网格后才能求解，网格质量的好坏直接决定了最终数值求解的精度，而网格生成的预处理耗费时间太大，在求解区域不规则或维数较高时，这些方法都有一定的困难.另一方面，在应用这些方法求解大变形、断裂问题或高维问题，特别是非定常问题，很多时候在求解的过程中都需要网格重构，这大大地增加了计算量，也严重降低了数值解的精度[1，2].为了解决这些问题，自适应网格方法是一个很好的选择，国内外许多学者在这方面进行了大量地研究[3-6].

同样是为了解决有限元方法等对网格依赖的问题，无网格方法近年来受到了很大的关注[7，8].这类方法试图彻底地或部分地消除网格.相对于网格依赖的数值方法，无网格方法具有一些明显的优点，因此在其出现后得到了日益众多的关注，并且一直是偏微分方程数值方法中的一个研究热点.一般说来，无网格方法基于一系列节点进行函数插值，与有限元等网格依赖的方法相比，避免了网格划分的预处理过程，也不会出现网格畸变的问题，对间断问题、解的变化较大的问题等具有较好的优势.另一方面，无网格方法只需各个节点的独立信息，而不需要单元之间的相互信息，数据结构简单.

利用径向基函数(Radial Basis Function， RBF)求解偏微分方程的方法，是最近几十年来备受关注的一类无网格方法[9].近年来，人们已经用RBF 方法求解了各种线性和非线性的偏微分方程，并且取得了不错的结果.其基本思想是在求解区域内根据所求解的问题布置节点，然后在每个节点上构造RBF，再将RBF 代入到所求解的偏微分方程，通过求解最终得到的代数方程获得近似解.与网格依赖的方法不同，RBF 方法不需要任何网格，对支撑域和边界没有要求，只需要以节点为中心的子域覆盖所求解区域即可.同时，RBF 与空间维数无关，仅依赖于节点间的距离，低维结果可以很容易推广到高维问题.事实上，RBF 是通过定义在[0，+∞)上的一元函数φ 与Rd上的欧几里德范数‖·‖来表示d 元函数φ(‖x-y‖)，其中x，y ∈Rd.因此用RBF 来处理多元问题具有效率高、储存方便、运算简单的特点.RBF 已广泛应用于计算几何、微分方程数值解、神经网络等领域.近年来，国内外学者对RBF 的理论与应用进行了系统的研究，随着RBF 理论的逐渐发展，目前已成为求解偏微分方程的一个强有力的工具[10-15].但是RBF 方法的缺点也是显而易见的，如理论方面很不完善，在逼近过程中所得到矩阵方程的系数矩阵是否可逆没有相关理论结果，也即数值解的唯一性还没解决；随着中心节点增加，需要求解一个很大的方程组，并且这个方程组经常是病态的；尚未见到开源或商业化的软件，后处理以及所得结果与其他软件的接口比较困难等等.为了解决这些问题，已经有学者考虑自适应的RBF 方法[16，17]，以及把有限元方法和RBF 方法相耦合的方法[18].

为了发挥无网格方法和网格依赖方法各自的优势，我们提出了一种基于径向基函数的自适应网格方法.利用有限元方法等数值结果结合径向基函数方法在求解区域内进行自适应配点，克服了有限元等方法计算中网格畸变和重新生成带来的困难，所得结果可以用有限元等方法的后处理技术进行分析.数值结果说明，所提方法产生的网格可以根据解的变化情况进行网格自适应，从而在保证相同数值求解精度的情况下可以极大地节省计算量.

2 径向基函数

径向基函数插值方法以其计算格式简单、节点配置灵活、精度高的特点而成为研究多元逼近理论的有利工具，并已经被应用于科学计算模拟和实际工程问题中.

径向函数满足以下条件[19]：如果‖x1‖ = ‖x2‖，就有φ(x1) = φ(x2)的函数φ，也即，仅依赖r = ‖x‖的函数(其中‖·‖为Euclid 范数).RBF 就是这样的函数空间：给定一个在定义域x ∈Rd上的一元函数φ:R+→R，所有形如Φ(x-c)=φ(‖x-c‖)及其线性组合张成的函数空间称为由函数φ 导出的RBF 空间.在一定的条件下，只要取{xj}两两不同，{Φ(x-xj)}就是线性无关的从而形成径向基函数空间中某子空间的一组基.当{xj}几乎充满R 时，{Φ(x-xj)}及其线性组合可以逼近几乎任何函数[9].

1) Kriging 方法的Gauss 分布函数(无限光滑)：φ(r)=exp(-βr2)， β ＞0.

2) Duchon 的thin plate(薄板)样条函数(分片光滑)：

3) Sobolev 样条函数：φ(r)=Kβ-d/2(r)rβ-d/2，其中K 为MacDonald 函数.

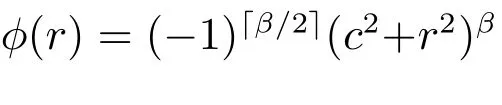
用RBF 求解偏微分方程的一般步骤如下：

对于偏微分方程

其中L 是偏微分算子，B 是边界算子.在Ω 内配置N 个离散的数据点r1，r2，··· ，rN，其中r1，r2，··· ，rl是内部节点，而rl+1，rl+2，··· ，rN是边界节点.设方程(2)的解u 可以用RBF 表示为

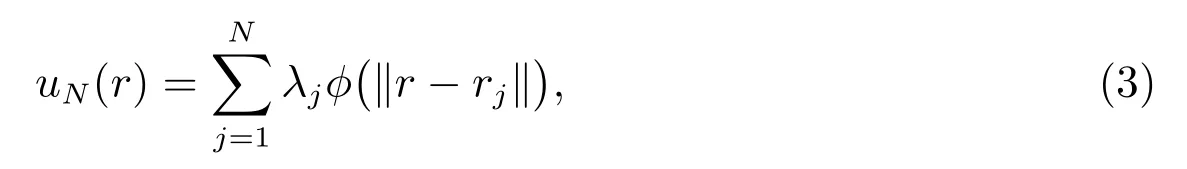
其中λ1，λ2，··· ，λN为待定系数.由(2)式和(3)式可得

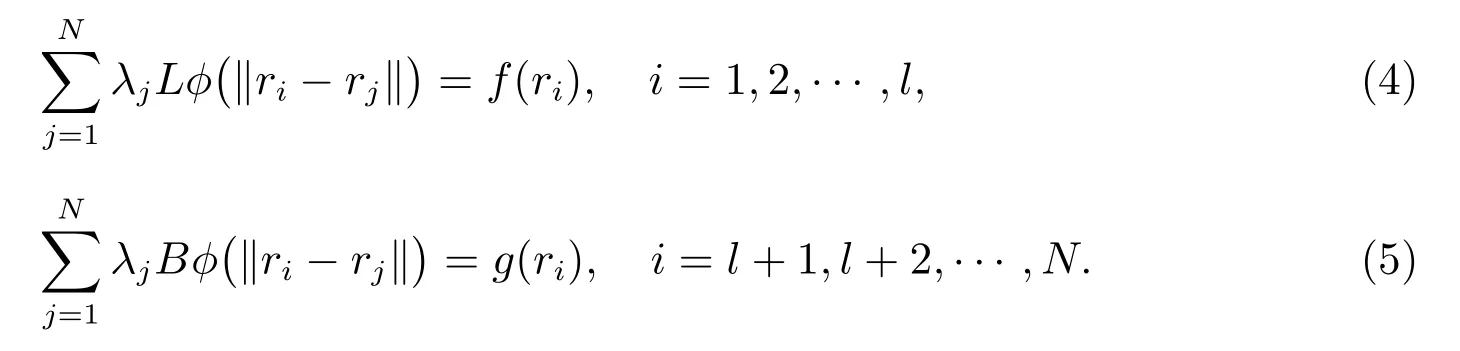
由(4)和(5)两式得到矩阵方程

其中

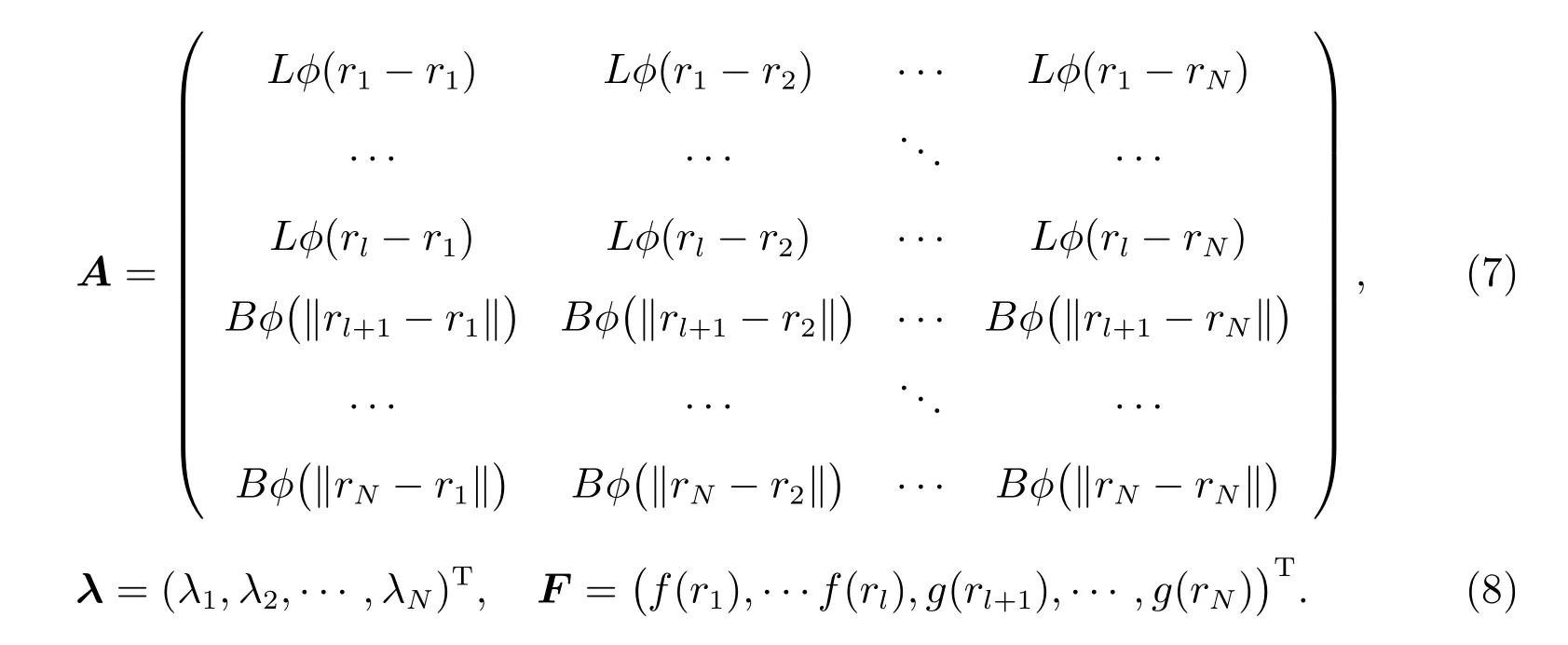
若矩阵A 是非奇异的，矩阵方程有唯一解，只要从(6)中解出λ，就可以得到方程(2)的近似解uN.

3 自适应网格方法

最早由Berger 和Oliger 于1984 年提出的自适应网格方法[20]，是一种高效且准确的数值方法.该方法抛弃了等距均匀的网格，代之以能够自动地适应所研究问题中解的特征的疏密程度不均的网格.其网格结构随着计算过程的推进而不断的动态改变，根据计算的实际需要以及问题的特性改变计算区域内的网格结构，在物理量变化比较剧烈的地方，例如：大变形、激波面、接触间断面和滑移面等，采用空间尺度较小的精细网格，在物理量变化缓慢的地方则采用空间尺度较大的粗网格，这样在保持计算高效率的同时得到高精度的数值解.

这一节我们给出一种简单、易于实现的自适应网格方法.该方法基于插值来调整RBF 的中心和参数，从而改变RBF 节点的分布.

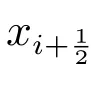
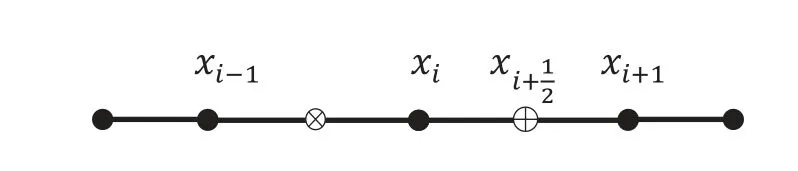
图1 网格自适应过程

对于二维问题来说，首先将求解区域进行有限元分割，然后进行有限元求解，与一维问题类似，用所得到的数值解可以求出方程(3)中的系数λi；接下来，可以用径向基和λi得到每个初始单元的中点(重心)处的值，用这个值与有限元解在这点的插值得到误差；误差超过给定阈值的点将成为新的节点，并且利用这个节点把所在的单元进行剖分；同样，若误差低于给定阈值，所在单元的节点都将被移除.

注1由于RBF 方法随着节点的增加计算量会显著上升，在误差大于给定阈值的单元可以多细化几次，但也不需要细化太多次.从我们的计算结果来看，细化两次就可以达到非常理想的效果.

注2同一个节点可能会同时作为细化和粗化单元的节点，我们是先进行细化，然后进行粗化.

注3另一种可以采用的方法是一次增加多个节点，但在这个过程中会增加计算量，特别是RBF 方法.

注4这里给出的自适应过程非常容易实施，并且可以推广到更高的维度.

对于某些偏微分方程问题来说，如果初始节点不是太多，上述过程还可以简化.如对于如下具有齐次Dirichlet 边值的Poisson 问题

方程组(6)变为

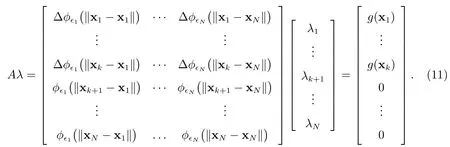
可以用RBF 方法直接求得系数λi.此时可以用如下公式

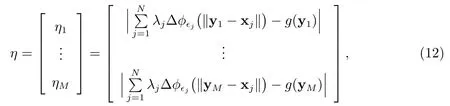
得到在节点{y1，y2，...，yM}处的误差，其中M 为RBF 的节点数.

4 数值算例

本算例考虑Burgers 方程的求解问题.Burgers 方程是偏微分方程中的一个非常重要的方程，广泛应用于各个领域，如流体力学、非线性、气体动力学、交通流等等.由于Burgers 方程是一个非线性方程，只有在很少的一些特殊情况下可以得到精确解，在更一般情形下，连数值求解都存在很大的困难.

我们考虑如下非定常Burgers 方程

其中Ω ⊂R2，∂Ω 是Ω 的边界，u =(u1，u2)是流体的速度.ν =1/Re(Re-Reynolds 数)是粘性系数，f 表示体积力，g 为已知函数.

设V =H1(Ω)2，则(13)-(15)的弱形式为：求u ∈V，使得

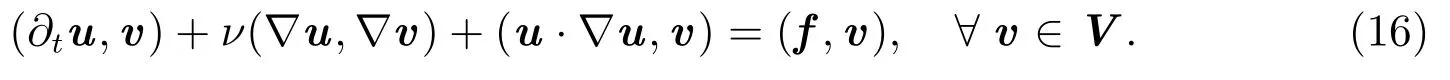
设Th是Ω 的一个三角剖分(h 是剖分参数)，Vh是有限元空间，Vh⊂V，则(16)的有限元解为：求uh∈Vh，使得

在下面的计算中，求解区域Ω=[0，1]×[0，1]， T =1，时间步长为Δt=0.01，

其中‖·‖表示欧氏范数，x =(x1，x2)， d =(0.3，0.3)， R=0.25.

本算例求解的过程中，当误差大于2×10-3时进行网格细化，小于2×10-6时进行网格粗化.粘性系数ν = 0.01.图2 至图4 分别给出了问题在时间t = 0， 0.5， 1 时的解.其中，图2(a)、图3(a)、图4(a)为RBF 节点分布；图2(b)、图3(b)、图4(b)为节点对应的有限元网格；图2(c)、图3(c)、图4(c)为网格对应的有限元解.其中为了看得清楚，有限元解的图片旋转了一个角度.

图2 t=0 时的解

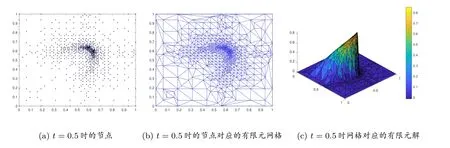
图3 t=0.5 时的解

图4 t=1 时的解

利用本文所提算法，在t = 0.5 时所用节点数和有限元网格单元数分别为656 个和1286 个，所用时间375.8368 秒.作为比较，我们用传统有限元方法在t=0.5 时对本问题进行了求解，所得结果如图5 所示：用相同节点数的均匀(粗)网格对Burgers 方程进行了求解，所得结果如图5(a)所示，可以看出所得结果非常粗糙，根本无法接受；用均匀加密(细)网格可以得到与图3(c)接近精度的解，如图5(b)所示，采用节点和有限元网格单元数分别为2704 个和5202 个，所用时间1184.7050 秒，大约是本文所提算法的3.15 倍.

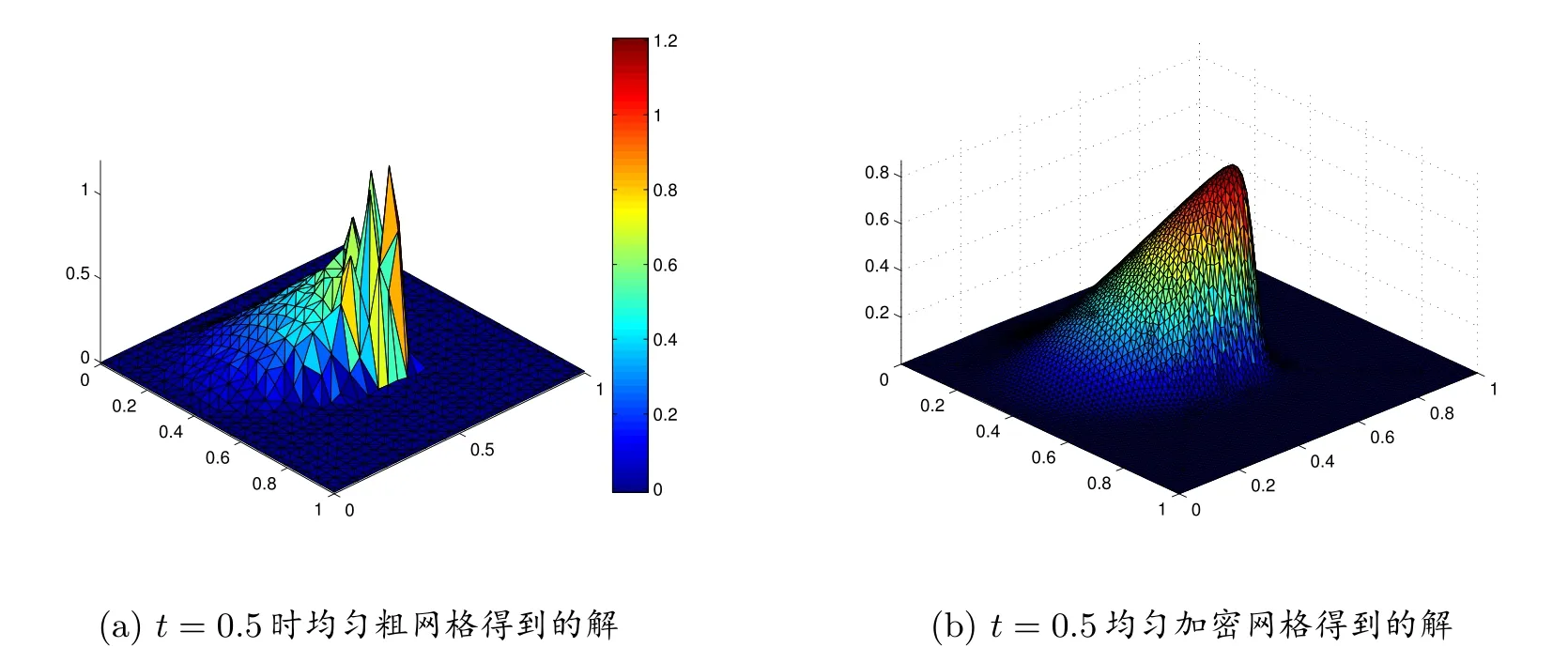
图5 传统有限元方法得到的解

从以上算例可以看出，本文所提算法可以在保持网格数量减少或不变的前提下较好的提高问题的求解精度，从而节省了求解时间.

5 结论

本文给出了一种求解偏微分方程的自适应网格方法，该方法把径向基函数计算格式简单、节点配置灵活的优点与网格依赖方法的稳健性很好地结合起来.该算法非常容易实施.数值算例也表明所提算法可以在解变化剧烈的区域加密网格，而在解变化平缓的地方粗化网格，从而可以保持较高精度的前提下减少或不增加计算量.我们用非定常Burgers 问题对算法进行的验证说明所提算法可以高效地求解偏微分方程问题.