面向对象多粒度概念格的构造

李克文， 吕萌萌， 邵明文

(中国石油大学(华东)计算机与通信工程学院，青岛 266580)

1 引言

德国Wille 教授于1982 年提出形式概念分析理论(Formal Concept Analysis， 简记为FCA)[1]，用于形式概念(外延(对象的集合)和内涵(属性的集合)组成的二元组)的发现、排序和显示，其核心数据结构是概念格结构模型.概念格是知识表现的一种模型，依据知识在内涵和外延上的依赖或因果关系建立概念层次结构，生动简洁地体现了概念之间的泛化和特化关系[2-4].形式概念分析是数据分析和知识处理有力的形式化工具，目前已成功应用于数据挖掘[5-7]、软件工程[8]等领域.

粒计算[9，10]起源于人工智能、粗糙集、商空间、概念格、模糊集等领域，通过构造和处理信息粒度，将复杂问题划分为一系列更容易处理的、更小的子问题，从而降低全局计算代价，进而从更高层次上对结果进行综合分析.Zadeh[11]于1979 年首次提出模糊信息粒后，在模糊集的基础上提出了粒计算的基本框架并强调粒度及其在推理中的重要性.近年来，粒计算已广泛应用于数据挖掘、模式识别与智能控制、复杂问题求解等诸多领域[12-16]，及当下较为前沿的研究热点，如时空、空间研究领域[17-19].

目前，已有许多专家学者对粒计算及相关领域进行了系统的研究，Yao[20-24]讨论了粒度的综合水平和粒计算理论.作为粒计算的模型之一，粗糙集理论[25]通过属性集合对论域进行目标概念的刻画，进行属性约简[26]、规则提取[27]与问题决策[28]等.Qian 等[29]基于多个粒结构提出了多粒度粗糙集模型，推广了粒计算的单粒度粗糙集模型，有助于获得信息系统的最满意决策或问题求解，充分体现了粒计算方法的丰富性和灵活性.Gu 等[30]研究了多粒度标记信息系统中的知识近似问题.Wu 和Leung[31]对多粒度决策表中的粒度标记块理论和应用进行了研究.基于多粒度标记信息系统对最优粒度的选择在文献[31-37]中进行了研究.基于多粒度粗糙集模型，Xu 等[38]研究了广义多粒度粗糙集以及最优粒度的选择问题.由此可知，粒计算领域的研究热点已经由单粒度问题过渡到更具有现实意义的多粒度问题.

概念格和粒计算的方法论在本质上具有相似之处，两种理论的结合研究已经引起了众多学者的关注.Du 等[39]对概念格与粒度划分的相关性进行了研究，分析了概念格与论域中的划分关系在概念描述与概念层次之间转换的关系.Belohlavek 和Sklenar[40]对形式概念格中的属性粒度进行研究.Kang 和Miao[41]对基于概念库的形式概念格属性粒度进行了分析，结合形式概念格的结构信息，在处理属性粒度时提出了上下确界，并提出了基于属性粒度的形式概念格扩展模型.张清华等[42]给出了概念知识粒与概念信息粒的相互转化方法.随后，Belohlavek 等[43]提出了属性粒度树，对属性粒度的粗细进行研究，同时提出了控制经典概念格中概念数量的Zoom 算法以实现多粒度经典概念格的快速构造，从而丰富了形式概念格中属性粒度的研究.Zou 等[44]提出了快速提升形式概念格属性粒度的“展开算法”.Wang 等[45]的研究内容从粒度优化问题过渡到多粒度联合求解的问题.

假设用户想用概念格的方法来分析商品的销售情况，可以用商品名称、商品销售的时间(上午、下午)、地域(东部、西部)、商品销售区域人们的收入水平(高于5000 元、低于5000 元)等描述商品的属性表示商品销售.属性粒度太大，描述对象太模糊，用户只得到很少的概念，无法提取有用的知识.类似地，若选择太小的属性粒度，可能会产生冗余概念，增大提取知识的成本.因此，通过不断改变属性的粒度得到不同的概念格，进而发现数据中潜在、有趣的知识自然成为一种迫切的需要.

综前所述，对概念格中的属性粒度进行研究具有重要意义.然而，当前只有经典概念格中的属性粒度变换研究，因此本文提出面向对象多粒度概念格的构造算法-Zoom，从而实现具有不同属性粒度组合的面向对象概念格的快速构造，同时附上实例演示帮助读者理解算法.

2 相关知识

2.1 形式背景和面向对象概念生成算子

定义1[46]记三元组(G，M，I)是形式背景，其中G 是非空的对象集合，M 是非空的属性集合，I 表示G 和M 之间的二元关系(I 是(G×M)的子集).

形式背景一般用二维表表示，行表示对象，列表示属性，行列交叉处的取值表示属性与对象的隶属关系，1 表示对象具有属性，0 表示对象不具有属性.

如表1 所示，对象的全集是{x1，x2，x3，x4，x5，x6}，属性的全集是{a，b，c，d，e}.第一行数据表示对象x1具有属性{a，c，d，e}，第一列数据表示属性a 由对象{x1，x2，x5，x6}所具有.

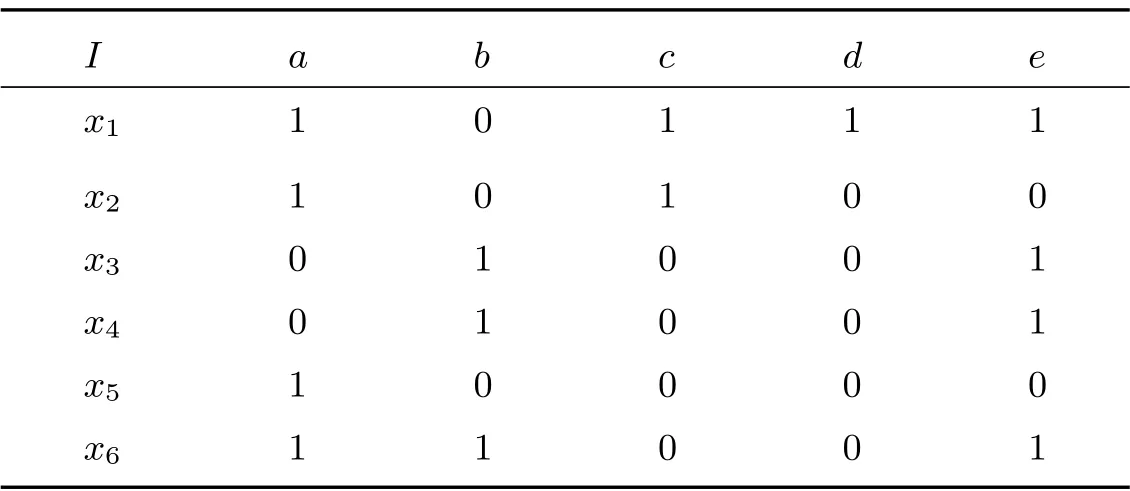
表1 形式背景(G，M，I)

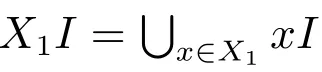
定义2[46]设(G，M，I)为形式背景，X ⊆G， B ⊆M，定义面向对象概念生成算子(↑，↓)，如下所示.

2G→2M：

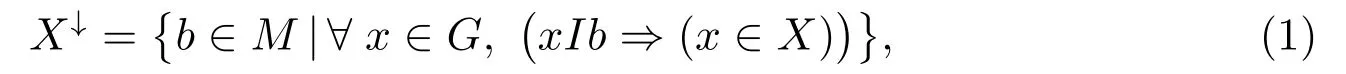
其中X↓表示只由X 中的对象拥有的属性组成的属性集合.

2M→2G：

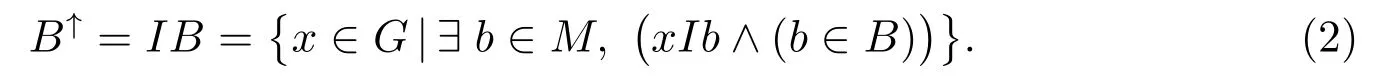
设X1，X2⊆G，算子(↑，↓)具有以下性质[46]：

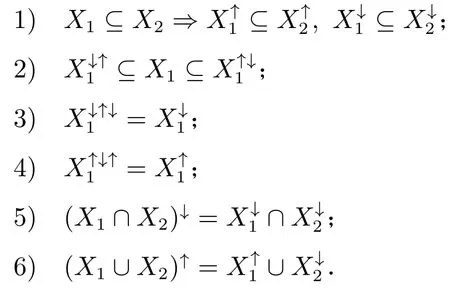
2.2 面向对象概念格

本小节介绍面向对象概念格的相关概念.

定义3[46]设(G，M，I)为形式背景，若对于任意的(X，B)， X ⊆G， B ⊆M， X =B↑， B =X↓，则称二元组(X，B)为面向对象概念.

设C1= (X1，B1)， C2= (X2，B2)是两个面向对象概念，如果X1⊆X2(B1⊆B2)，则记(X1，B1) ≤(X2，B2).若∄C0= (X0，B0)，使得(X1，B1) ≤(X0，B0) ≤(X2，B2)，则称(X1，B1)是(X2，B2)的直接子概念，(X2，B2)是(X1，B1)的直接父概念，形式概念之间的这种关系称为概念之间的偏序关系用“≤”表示.

定义4[46]设(X1，B1)， (X2，B2)为面向对象概念，面向对象概念间的交(∧)、并(∨)运算如下

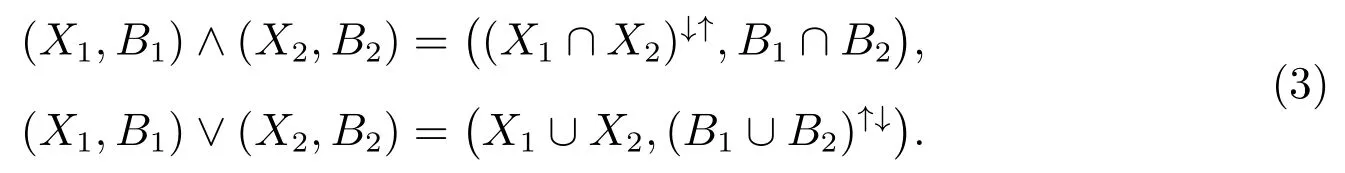
由表1 所示的形式背景，得到如图1 所示的面向对象概念(格节点)及概念格.其中，概念的外延为对象(此处用形式背景中对象的右下数字表示)集合，内涵为属性(此处用字母表示)集合.

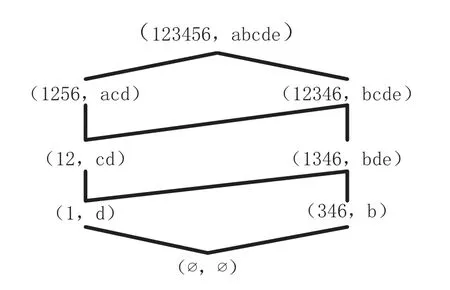
图1 面向对象概念格

2.3 属性粒度

在计算机领域，粒度是指保存数据的细化或综合程度.在不同属性粒度的转换过程中，发现最优粒度是粒计算的一个重要应用.属性粒度越小，描述对象越细致.例如，一个属性“Grade”([0-100] points)可以细分到另一个属性粒度的级别：{“Fail”([0-60)points)，“Pass”([60-100]points)}，继续细分到下一个属性粒度的级别：{“Worse”([0-30) points)，“Bad”([30-60) points)，“Good”([60-90) points)，“Good”([90-100] points)}.

下面引入粒度树及相关定义.

定义5[43]用一个树根为Z 的树形结构表示属性Z 的粒度等级，称具有以下特点的树形结构为属性Z 的粒度树：

1) 树根是粒度最大的属性Z，树的每一个节点都有一个独一无二的标签Zi；

3) 如果{z1，z2，··· ，zi，zi+1，··· ，zn}是粒度大小相同的粒子的全集(粒度树的一个粒层)，且满足以下三个条件，则称{z1，z2，··· ，zi，zi+1，··· ，zn}是Zi的一个划分：

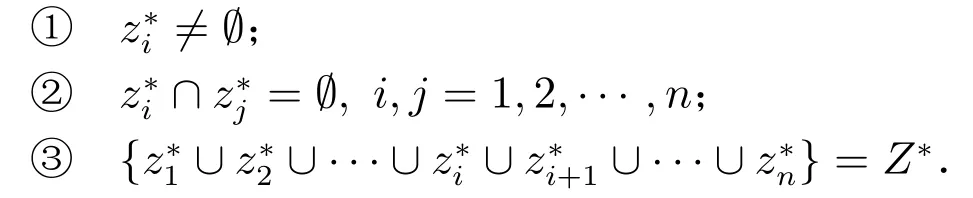
如图2 所示，属性成绩的粒度树共有3 个粒层，分别是：{{Grade}， {Pass， Fail}，{Worse， Bad， Good， Excellent}}.

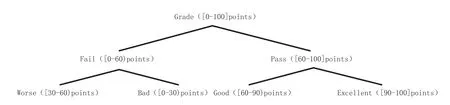
图2 “Good”的粒度树

设(G，M，I)为形式背景，

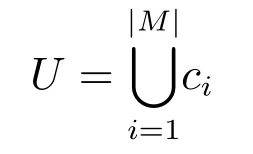
表示由每个属性的一个粒层组合在一起形成的粒层集合，其中ci表示第i 个属性的粒度层级，|M|表示(G，M，I)中属性的个数.

同一形式背景中属性的不同粒层集合之间存在一种偏序关系，设

基于属性不同的粒层组合可以得到不同的形式背景(G，MU，IU)，设U1={L，R，G}， U2={L，R，{lG，dG}}，由此得到如表2 所示的两个形式背景(G，MU1，IU1)(左)、(G，MU2，IU2)(右).其中{G}， {lG，dG}是属性“Green”的粒度树的两个粒层，且{lG，dG}≤{G}.

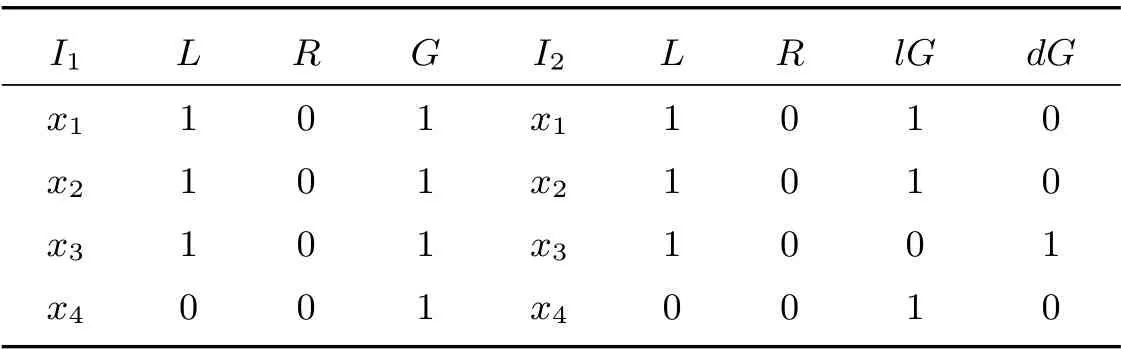
表2 形式背景(G，M，I)

3 面向对象多粒度概念格的构造算法—Zoom

属性粒度改变前后，概念格中的概念存在内在联系，为了方便研究概念格变化的规律，现作以下定义：

3.1 面向对象多粒度概念格的属性粒度细化算法-Zoom-in

3.2 面向对象多粒度概念格的属性粒度粗化算法-Zoom-out

由此，Zoom-out 的正确性得证.

以上是针对面向对象概念提出的Zoom 算法，通过类似于面向对象概念的相关定理易于得到面向属性概念的相关定理及面向属性概念格的Zoom 算法.在经典的概念格构造算法中，消耗时间最多的步骤是每层概念两两运算得到新概念，设每层概念的个数为N，则经典概念格的构造算法时间复杂度为O(N2)，而Zoom 算法是在原有概念格的基础上对每个概念格的内涵与外延单独进行计算，所以时间复杂度为O(N)，因此，与经典概念格的构造算法相比，Zoom 算法的时间复杂度较低，因此执行效率更高，有助于在实际应用中从数据中进行知识的挖掘.

4 结语

属性粒度对于从数据中提取概念进而得到概念格的结构有重要影响，选择合适的属性粒度水平进行组合，可以有效的控制概念格中概念的数量，进而有助于用户发现有趣的知识.对于属性粒度水平的选择依赖于领域专家的经验知识.通过分析概念内涵、外延在属性粒度变化前后的关系，对原概念格的概念进行分类，在此基础上，我们提出的算法-Zoom 可以在已有概念格和粒度树的基础上直接实现面向对象概念格的构造，避免了利用传统概念格构造算法从形式背景生成概念继而得到概念格的繁重工作量，从而提高了概念格的构造效率.下一步，我们将研究面向属性多粒度概念格的构造以及面向对象多粒度概念格、面向属性多粒度概念格、经典概念格之间的转换关系，后续将研究多粒度广义单边概念格的快速构造算法.