人口普查漏报估计研究

胡桂华， 廖金盆， 范署姗， 叶宝红， 吴 婷

(重庆工商大学数学与统计学院 经济社会应用统计重庆市重点实验室，重庆 400067)

1 引言

2020 年，中国、美国和其他许多国家将进行人口普查及其质量评估.普查漏报是评估目标之一.为指导各国政府统计部门开展普查漏报评估工作，联合国统计司组织世界人口普查质量评估专家撰写人口普查质量评估工作指南.该指南中的未匹配估计量只是包括了在质量评估调查中登记而未在普查中登记的漏报人口，从而低估总体普查漏报人口数.

为解决上述问题，本文在对现行普查漏报估计方法研究的基础上，提出普查漏报合成估计量.该估计量由两部分构成.第一部分是三个线性漏报估计量，估计未登记在普查人口名单但至少登记在质量评估调查人口名单及行政记录人口名单之一的人数.第二部分是缺失单元漏报估计量，估计未登记在任何名单的人数.

创新体现在两个方面.第一，相比目前国内外采用的估计普查漏报的逆记录检查估计量、未匹配估计量和平衡推算估计量，普查漏报合成估计量通过引入人口行政记录，可以找到更多的普查漏报人口.首先，逆记录检查，需要在本次全国人口普查微观数据库搜索漏报人口，这是一项十分艰难的工作，而普查漏报合成估计量，只需要比对同一样本普查小区的普查人口名单、质量评估调查人口名单及行政记录人口名单，便可以获得样本漏报人口，工作难度小许多.其次，未匹配估计量，未包括同时遗漏于普查人口名单及质量评估调查人口名单的漏报人口，而普查漏报合成估计量同时包括遗漏于上述三份人口名单的人口.再次，平衡推算估计量，只能算出普查漏报人口数，而不能解释形成漏报的原因及其漏报的程度，而普查漏报合成估计量，在比对三份人口名单后，可查明普查漏报的原因、程度及漏报在总体中的分布情况.探索普查漏报的发生机制，是漏报估计的主要目的.相比中国2010 年采用的未匹配估计量计算的样本普查漏报率，普查漏报合成估计量，利用抽样权数将样本扩张到总体，估计总体的普查漏报率，并且采取刀切法近似计算抽样方差.第二，在有限总体概率抽样条件下，普查漏报的总体指标需要用样本来估计.本文给出估计量的构造方法以及估计量的方差估计方法.

2 文献综述

普查覆盖误差包括普查净误差、普查多报与漏报[1].净误差定义为总体实际人数与普查登记人数之差.各国目前通行的做法是，用基于“捕获-再捕获”模型的双系统估计量[2]构造总体实际人数估计量，把这个估计量与普查登记人口数之差当作人口普查净误差.未来可能用基于三次捕获模型[3，4]的三系统估计量[5-7]来取代双系统估计量[8-10].

净误差估计的研究成果多于普查漏报与多报.政府统计部门在其所发布的人口普查质量评估工作报告中只是简单提及普查漏报的估计方法或估计结果.研究普查漏报估计的学术论文甚少.漏报有两个特点.一是漏报人口未登记在普查表中，从普查表中得不到漏报人口信息，要构造漏报估计量，需要采取间接估计方法.二是各国人口普查质量评估结果显示，普查漏报比多报严重.

逆记录检查估计量、未匹配估计量和平衡推算估计量，是估计总体普查漏报人口的传统方法[11].采用逆记录检查估计量的国家包括加拿大、丹麦、芬兰、危地马拉、洪都拉斯、以色列、意大利、荷兰、挪威、瑞典和美国.逆记录检查抽样框由上次普查登记人口、上次普查漏报人口、上次到本次普查出生及迁入人口组成.样本由人构成.对每一个样本个人，在本次全国普查微观数据库搜索，寻找与其相同的人.如果找到，就称该样本个人为匹配人口，否则称为未匹配人口，即普查漏报人口.逆记录检查估计量为样本个人与其抽样权数的线性估计量.其优势是，由于逆记录检查与本次普查独立，因而避免了因这两项调查不独立引起的交互作用偏差而低估或高估普查漏报人口数.其劣势是自上次普查之后，样本个人可能已经离开原来居住的地方，或者死亡、更改了姓名，找到他们有困难，难以判断这些人是在本次普查中登记，还是漏报，或不属于应该在本次普查中登记的人.这增加了逆记录检查实施的难度和错误判断样本个人在普查中登记情况的风险.

未匹配估计量为质量评估调查未匹配人口与其抽样权数的线性估计量，或者质量评估调查人口数估计量与其匹配人口数估计量之差.匹配人口指，同时登记在质量评估调查名单与普查名单的人口.未匹配人口指，只登记在质量评估调查名单的人口.联合国统计司建议各国使用未匹配估计量.中国在2010 年使用该漏报估计量估计现有人口、户籍人口及常住人口的漏报率[12].未匹配估计量优势在于，容易理解和实施.其劣势是未包括同时遗漏于这两份名单的人口，从而低估总体普查漏报人口数.如果样本中的未匹配人口过少甚至为零，该漏报估计量提供的总体漏报人口数估计值可能严重偏离真值.

平衡推算估计量，依据公式“估计的净误差+估算的普查登记人口数=估计的普查漏报人数-估计的普查多报人数”间接推出总体普查漏报人口数[13].在人口普查中，有些住户拒绝填写普查表，或拒绝普查员上门登记.这类住户的人口数一般通过邻居，或其他熟悉情况的人估算.美国普查局把估算的普查登记人数，计入普查登记人口总数.美国在2010 年普查漏报估计中，在获得净误差估计值(-3.6 万人)、估算的普查登记人口数(599.2 万人)，以及估计的普查多报人口数(1004.2 万人)后，得到估计的普查漏报人口数为1599.8 万人(Vincent Thomas Mule， 2012).平衡推算估计量的优势是，可以很方便地推出普查漏报人口数.其缺陷有4 个：

① 不能提供本次普查登记过程中的漏报人口信息，不利于下次普查及其质量评估工作方案的改进；

② 净误差与普查多报估计对普查正确登记位置认定标准不一致，即前者要求每个人登记在其所属的样本小区，或其周围区域内，而后者可以登记在研究区域的任何地方.这种不一致影响普查漏报估计精度；

③ 内含交互作用偏差的双系统估计量估计的净误差存在一定程度的偏误，这种偏误造成叠加效应，影响普查漏报估计精度；

④ 估算的普查登记人口数存在一定程度的估算误差，降低普查漏报估计精度.

从对普查漏报合成估计量创新情况的论述，以及对现有普查漏报估计量利弊的分析，不难看出，普查漏报合成估计量是一种相对较为理想的普查漏报估计方法，有望应用于人口普查漏报估计.中国计划在2020 年首次使用普查漏报合成估计量.

3 普查漏报合成估计量理论

为构造普查漏报合成估计量，在获得普查人口名单、质量评估调查人口名单及行政记录人口名单后，要做好五项工作.第一，每份名单只能登记普查目标总体的人.如果有的名单重复登记或登记普查标准时点不存在的人，就予以剔除.行政记录人口名单要利用多个来源的人口名单建立，并剔除其中的重复人口.对名单中存在但怀疑可能已经死亡的人，在现场核实的基础上决定剔除还是保留.第二，分析普查漏报的可能情形，即只登记在质量评估调查或行政记录的人口(共3 种)，未登记在任何名单的人口(1 种).其中，前3 种漏报人口数使用线性漏报估计量估计，后1 种漏报人口数采用缺失单元漏报估计量估计.普查漏报合成估计量为三个线性漏报估计量与一个缺失单元漏报估计量[14-16]的总和.第三，比对三份人口名单，为构造三个线性漏报估计量及一个缺失单元漏报估计量提供数据.假定不存在比对误差，否则要测算比对误差对普查漏报合成估计量的影响.第四，采用加权优比排序法[17]，选择对总体人口等概率分层的变量，例如，性别、年龄、房屋所有权、居住地点、民族，把登记概率大致相等的人口放在同一层.显然，变量越多，交叉层的层数也越多，分配到每一个交叉层的样本人口就越少，普查漏报估计值的抽样误差就越大[18].为控制交叉层数目，分层变量的数目应该减少.分层变量的选择是一项复杂的工作，超出本文研究范围.对此问题有兴趣的读者，请见参考文献[17].把每一个交叉层称之为等概率人口层.在每个等概率人口层，建立普查漏报合成估计量及其抽样方差估计量.汇总所有等概率人口层的普查漏报合成估计量，得到总体的普查漏报合成估计量.汇总所有等概率人口层的普查漏报合成估计量的抽样方差及等概率人口层之间的协方差，得到总体的普查漏报合成估计量的抽样方差.等概率人口层之间的协方差可能为正或为负.第五，构造三份名单全面登记、抽样登记、人口移动和无人口移动的缺失单元漏报估计量、线性漏报估计量及普查漏报合成估计量.

用v 表示任意等概率人口层，V 为总层数.为了叙述方便，在下面的式(1)-(26)省去v.在构造总体普查漏报估计量时，在式(27)-(30)添加v 和V.

用xcqa表示等概率人口层的人口登记在三份名单的人口数，下标c， q， a 分别表示普查、质量评估调查和人口行政记录，取值1 或0.c=1 表示等概率人口层的人口在普查人口名单，c=0 表示等概率人口层的人口不在普查人口名单.q =1 表示等概率人口层的人口在质量评估调查人口名单，q =0 表示层v 的人口不在质量评估调查人口名单.a=1 表示等概率人口层的人口在行政记录人口名单，a = 0 表示层v 的人口不在行政记录人口名单.用这些记号写出如下有关的估计量.

3.1 等概率人口层的缺失单元漏报估计量

我们分三个层次讨论问题.第一层次，假定普查人口名单、质量评估调查人口名单及行政记录人口名单是对总体人口的全面登记，并且三份名单所登记的是各小区普查时点的同一常住人口总体.第二层次，仍假定三份名单对总体全面登记，并考虑普查日与质量评估调查日之间的人口移动.第三层次，用有限总体概率样本资料，构造上面两个层次的缺失单元漏报估计量的构成元素的估计量[19].

3.1.1 全面登记且无人口移动的缺失单元漏报估计量

缺失单元漏报估计量，依据普查人口名单、质量评估调查人口名单及行政记录人口名单的统计关系建立.三份名单可能的统计关系分为四类.第一类是三份名单条件独立.例如，普查与质量评估调查相关，质量评估调查与人口行政记录相关，普查与行政记录独立.这类关系共有3 种.第二类是三份名单联合独立.例如，普查与质量评估调查相关，这两项调查与行政记录独立.这类关系也有3 种.第三类是三份名单两两相关，这类关系有1 种.第四类为三份名单相互独立，这类关系有1 种.

构造缺失单元漏报估计量有两个方法.第一个方法是，用三系统估计量构造三份名单的缺失单元漏报估计量.由于三系统估计量在三个名单统计关系不同的情况下有不同的计算公式，所以需要先使用对数线性模型，判断三份名单属于何种统计关系，然后使用该种统计关系下的三系统估计量计算公式.第二个方法是，根据先验信息分析三份名单最可能形成的统计关系，并只构造这种统计关系的缺失单元估计量.普查与质量评估调查相关，但它们与人口行政记录独立，这种统计关系的可能性大.事实上，这两项调查由政府统计部门组织实施，而人口行政记录来源于不同于政府统计部门的行政部门.另外，这两项调查的目的是为了获得人口数，而人口行政记录是行政工作的副产品，用于行政管理.例如，我国户籍资料本身并不是为了提供人口数，而是为了实现对人的管理，控制人口向大城市流动，合理布局全国人口分布.基于此种分析，只构造该种统计关系的缺失单元漏报估计量.为构造缺失单元普查漏报估计量，需要把普查和质量评估调查合并在一起当作第一个来源，把人口行政记录当作第二个来源.由于数据来源的特点，它们合并后独立于人口行政记录.不在第一个来源但在第二个来源的人口数用x001表示，在第一个来源不在第二个来源的人口数用(x110+x100+x010)表示，同时在两个来源的人口数用(x111+x101+x011)表示，未登记在任何来源的人口数用x000表示，其估计量称为缺失单元漏报估计量，用^x000表示.把这四项填写在表1.

表1 两来源的等概率人口层数量

式(1)中的n=x111+x101+x011+x110+x100+x010+x001.总体中的人至少在两个来源之一的概率为[1-(1-π1+)(1-π+1)].单元(i，j)人数的另外一种表达式为概率函数的二项分布为

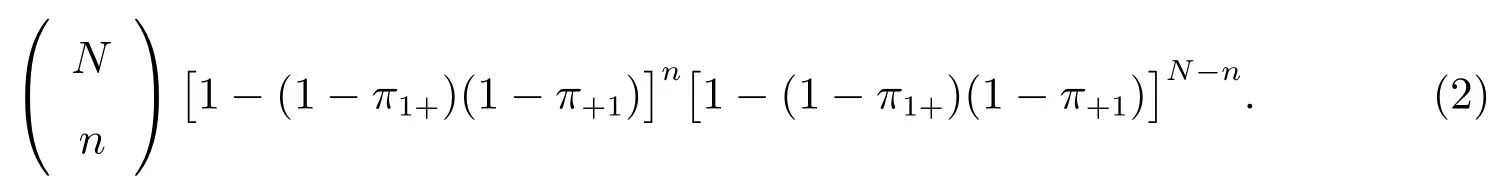
如果给出π1+， π+1， Nv，那么π1+， π+1的最大似然估计量分别为

式(3)中，n+1=n11+n01， n1+=n11+n10.

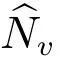
由于N =n+x000，所以

将式(4)及n 代入式(5)得到

式(6)是三份名单对总体全面登记的缺失单元估计量.

3.1.2 全面登记且人口移动的缺失单元漏报估计量

在人口普查质量评估中，质量评估调查通常滞后于人口普查半个月左右.在这期间，会有人从其他普查小区移动到本小区，也有人从本小区移动到其他小区，还有人一直居住在本小区.把这三种情况的人分别称为向内移动人口、向外移动人口和无移动人口.质量评估调查人口名单的人口有两种构成方式.一是无移动人口和向外移动人口，简称质量评估调查-A.另外一种方式是无移动人口和向内移动人口，简称质量评估调查-B.质量评估调查-A 的优势是实现了人口普查质量评估追溯普查标准时点的人口及其人数的目的，缺点是找到向外移动人口有难度，其有关信息只能通过邻居或估算方法获得，误差较大.质量评估调查-B 的优势是向内移动人口在本小区，获取其质量评估调查时信息较容易，劣势是获得其普查标准时点在其他普查小区的信息有一定困难.如果采用质量评估调查-A，那么式(6)中的每项人口数要更改为无移动人口数与向外移动人口数的和.如果采用质量评估调查-B，那么式(6)中的每个人口数要更改为无移动人口数与向内移动人口数的和.用n， i， o 分别表示无移动人口、向内移动人口和向外移动人口.

如果采取质量评估调查-A，那么式(6)变为

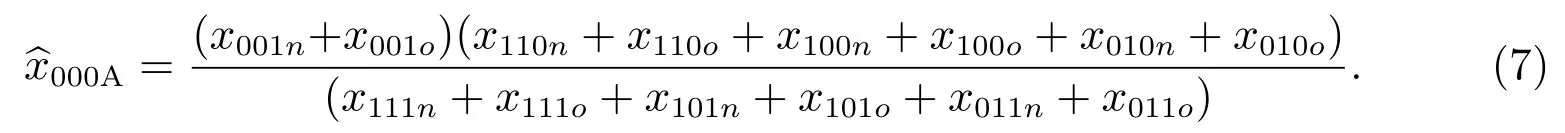
对本小区，向外移动人口在质量评估调查标准时点前已经离开了本小区，不可能登记在本小区的质量评估调查人口名单中，因此式(7)变为

如果采用质量评估调查-B，那么式(6)变为

同样，对本小区，向内移动人口无法登记在本小区的行政记录人口名单，因此式(9)变为

3.1.3 抽样登记且人口移动的缺失单元漏报估计量

在质量评估调查为全面调查情况下，以上各式等号右边的每一数据项都是层v 的总人口数指标.为了节约成本、时间，减少非抽样误差，各国政府统计部门的质量评估调查实际上是从全国或各省或各行政区的普查小区总体中抽取样本普查小区来进行的.在质量评估调查为抽样调查及考虑人口移动情况下，式(8)和式(10)的每一数据项要用估计量来表示，用有限总体概率样本来构造，即先将每一样本小区的人口数与其抽样权数相乘，然后相加.如果对样本小区人口100%抽样，而且不存在无答复，那么样本普查小区的抽样权数等于其中每人的抽样权数.此时式(8)变为

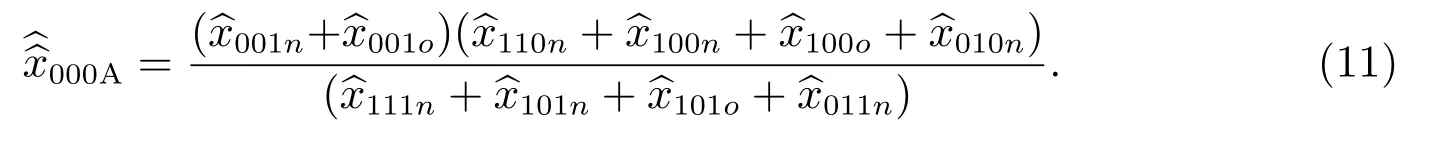
式(10)变为

3.2 等概率人口层的线性漏报估计量

3.3 等概率人口层的普查漏报合成估计量

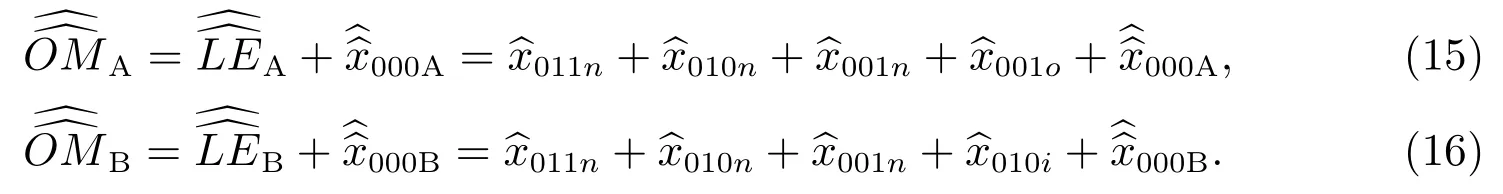
式(11)-(16)等号右边的每一个估计量，依据质量评估调查样本数据来计算.在人口普查质量评估抽样调查中，样本的抽取方法有分层整群抽样、分层多阶段抽样和分层多重抽样[20-22].中国自1982 年人口普查质量评估起，一直采用分层整群抽样方法抽取普查小区样本.本着研究服务于应用的原则，本文采取分层整群抽样.在该抽样法下，式(11)-(16)的每一个估计量统一用式(17)来表示.

式(17)中，H 表示对总体全部普查小区所分的层数，例如按照普查小区规模将总体中的所有普查小区分在三层，每一层h 的样本规模记为nh， h = 1，2，··· ，H，yhi为小区hi 在等概率人口层的人数.在分层整群等概率抽样下，样本普查小区hi 的抽样权数whi为

3.4 等概率人口层的普查漏报合成估计量的抽样方差估计量

式(11)和(12)，以及式(15)和(16)的复制估计量分别为

式(15)和(16)的分层刀切抽样方差(variance， 缩写为var)估计量分别为

为了正确理解及使用式(25)和式(26)，需要注意两点.第一，刀切法仅在样本内操作.切掉一个单位，只不过是这个切掉的单位不在样本中，并不意味着它不在总体中.如果把这个单位从总体中切掉，调查对象就改变了，就不再是原来的总体了，与现在的调查任务就不一样，所以从样本中切掉一个单位，只不过是假定了一个虚拟样本，即切掉的那个单位没有进入这个虚拟样本.就未分层整群抽样来说，假定从单位数为N 的总体中简单随机抽取单位数n.现在从该样本中切掉1 个单位，在计算其它(n-1)个单位各自的复制权数时，应该是从N 个单位中简单随机抽取(n-1)个单位概率的倒数，此时总体单位数目不改变，只是样本单位数目减去1.即这(n-1)个单位此时各自的复制权数是N/(n-1).第二，同计算复杂总体参数估计量抽样方差的泰勒线性方差估计量相比[25，26]，刀切法操作便利，容易实施，在计算了样本普查小区的复制权数及总体参数估计量的复制估计量后，将样本数据代入其中即可算出结果.

3.5 总体普查漏报合成估计量及其抽样方差估计量

在构造了每个等概率人口层(用v 表示)的普查漏报估计量后，下一步要做的工作是汇总所有等概率人口层(用V 表示总层数)的普查漏报合成估计量及其抽样方差估计量，得到总体的普查漏报合成估计量及抽样方差估计量.

4 未匹配估计量

为了比对普查漏报合成估计量与传统普查漏报估计量在数据估计精度上的优势，以及考虑进行这种比对所需数据资料的可得性，我们现在讨论未匹配估计量.除美国等少数几个国家外，其他国家都是使用这种估计量.与普查漏报合成估计量相比，未匹配估计量不用对总体人口等概率分层，直接在总体人口内构造及使用.

未匹配估计量建立的关键是获得匹配人口.对样本普查小区的普查人口名单及质量评估调查人口名单，如果后者名单中的某人出现在普查人口名单，就称其为质量评估调查人口名单的匹配人口，如果后者名单中的某人未在普查人口名单中出现，就称为后者的未匹配人口[27].未匹配人口为普查漏报人口.做出上述判断的一个假定条件是，质量评估调查人口名单中的每一个人属于普查目标总体，应该在普查中登记.在人口普查质量评估中，各国政府统计部门默认质量评估调查人口名单完美无缺.

为区别普查漏报合成估计量的总体P，这里用U 表示总体的未匹配估计量.

4.1 总体未匹配估计量

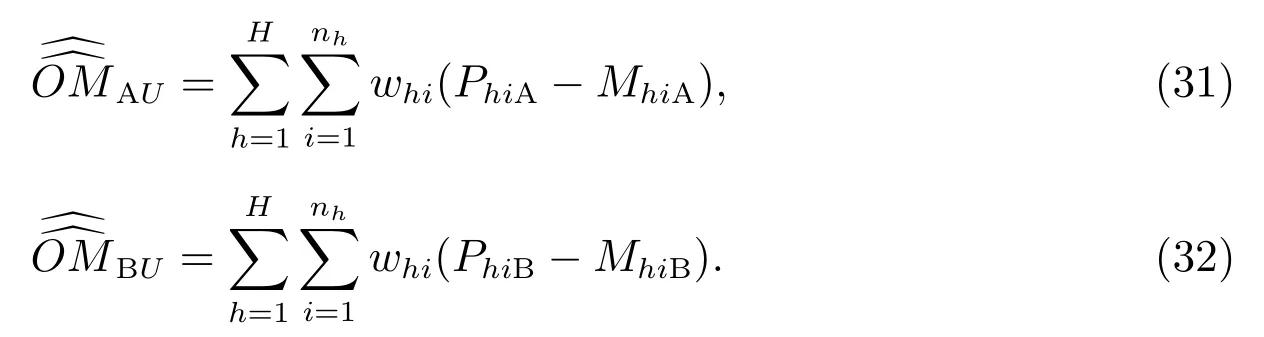
式(31)和(32)，PhiA和MhiA分别表示质量评估调查-A 的无移动人口和向外移动人口的数目之和，以及它们的匹配无移动人口和向外移动人口的数目之和；PhiB和MhiB有同样的相应解释.whi依据式(18)计算.

4.2 总体未匹配估计量的抽样方差估计量

虽然式(31)和式(32)有方差数学表达式计算其抽样方差，但为了与普查漏报合成估计量的抽样方差进行数据上的可比性比较，我们使用分层刀切法近似计算其抽样方差.文献[19]指出，线性估计量的抽样方差可以用分层刀切法计算.

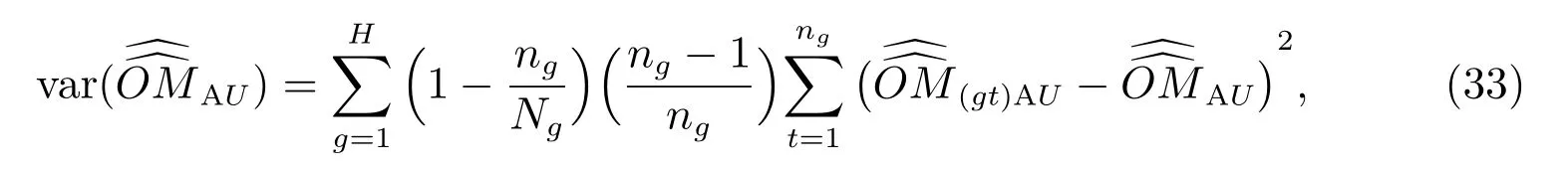
式(34)和(36)中的whi(gt)根据式(19)计算.不难看出，未匹配估计量的抽样方差计算，无需在等概率人口层内进行，可以直接在总体内计算.

5 实证分析

实证对象为广西南宁市邕宁区，资料所属时间是2010 年11 月1 日零时，目标是估计邕宁区普查漏报.在样本抽取前，将邕宁区所有普查小区划分在三层：蒲津社区层；那楼社区和新江社区合并层；百济社区和中和社区合并层.在每层，以普查小区为抽样单位，从邕宁区的1038 个普查小区中简单随机抽取7 个，并获得了样本小区的普查人口名单、质量评估调查人口名单和行政记录人口名单.通过比对，获得同时登记在三份名单、两份名单及一份名单的人口数.对每个样本小区的人口，按照性别分在两个等概率人口层，即男性层和女性层.在这两个层计算普查漏报估计值.

5.1 基于普查漏报合成估计量的估计结果及数据分析

5.1.1 样本资料

样本普查小区及样本人口数资料见表2 至表5.

5.1.2 加权人数计算

利用表2 至表5 样本数据，使用式(17)计算式(11)和(12)，以及式(15)和(16)每项的加权人数，见表6.

表2 分层及样本

表3 样本普查小区人口数

表4 样本普查小区男性在三份名单登记的人数(人)

表5 样本普查小区女性在三份名单登记的人数(人)

续表5 样本普查小区女性在三份名单登记的人数(人)

表6 等概率人口层在三份人口名单每项的加权人数(人)

5.1.3 普查漏报计算

使用式(22)-(24)，利用表6 数据，计算男性层和女性层的普查漏报人数.利用式(27)-(29)计算总体普查漏报人口数.计算结果见表7.

表7 表明，如果采取质量评估调查-A，男性层和女性层的普查漏报人口数分别为5107 人和6339 人.如果采取质量评估调查-B，男性层和女性层的普查漏报人口数分别为4477 人和4707 人.如果采取质量评估调查-A 或-B，总体普查漏报人口数分别为11446 人或9184 人.因此，无论男性层、女性层，还是总体，质量评估调查-A 的普查漏报人口数均大于质量评估调查-B.这一现象表明，所选取的样本普查小区的向外移动人口多于向内移动人口.由于样本小区是随机选取的，所以邕宁区的向外移动人口比向内移动人口多.“六普”数据分析显示，广西南宁市邕宁区的一些中青年去广东、北京、上海、浙江、深圳打工，而来邕宁区打工的很少.在普查与质量评估调查之间，邕宁区人口也是以向外移动为主.可见，本文计算结果与“六普”结果一致.

表7 普查漏报人数(人)

5.1.4 普查漏报估计值的抽样方差计算

在计算了男性和女性及总体的普查漏报估计值之后，还要使用分层刀切法计算其抽样方差估计值.这包括三个步骤.第一步，使用式(19)计算每刀切掉每一层的每一个样本普查小区后，所有样本普查小区的复制权数，计算结果见表8.在分层整群抽样下，刀切对象是每一层的所有样本普查小区.如果采取整群二重抽样，刀切的对象是第一重样本的所有普查小区，而不是第二重样本的所有普查小区.第二步，依据式(20)计算式(21)-(24)每一个数据项的复制估计量，例如刀切第一层的第一个样本普查小区A1 后的每一个数据项的复制估计量，计算结果见表9.为节省篇幅，省去依次刀切A2-A7 样本普查小区后得到的每个数据项.利用表9 数据，使用式(21)-(24)计算“缺失单元人数复制值及漏报复制值”，计算结果见表10.为了计算普查漏报抽样方差，写出依次刀切A1-A7 的普查漏报复制估计值及普查漏报估计值，见表11.第三步，利用表11 数据，使用式(25)、式(26)、式(28)、式(30)计算男性层、女性层，以及总体的抽样方差与协方差.结果请见表12.

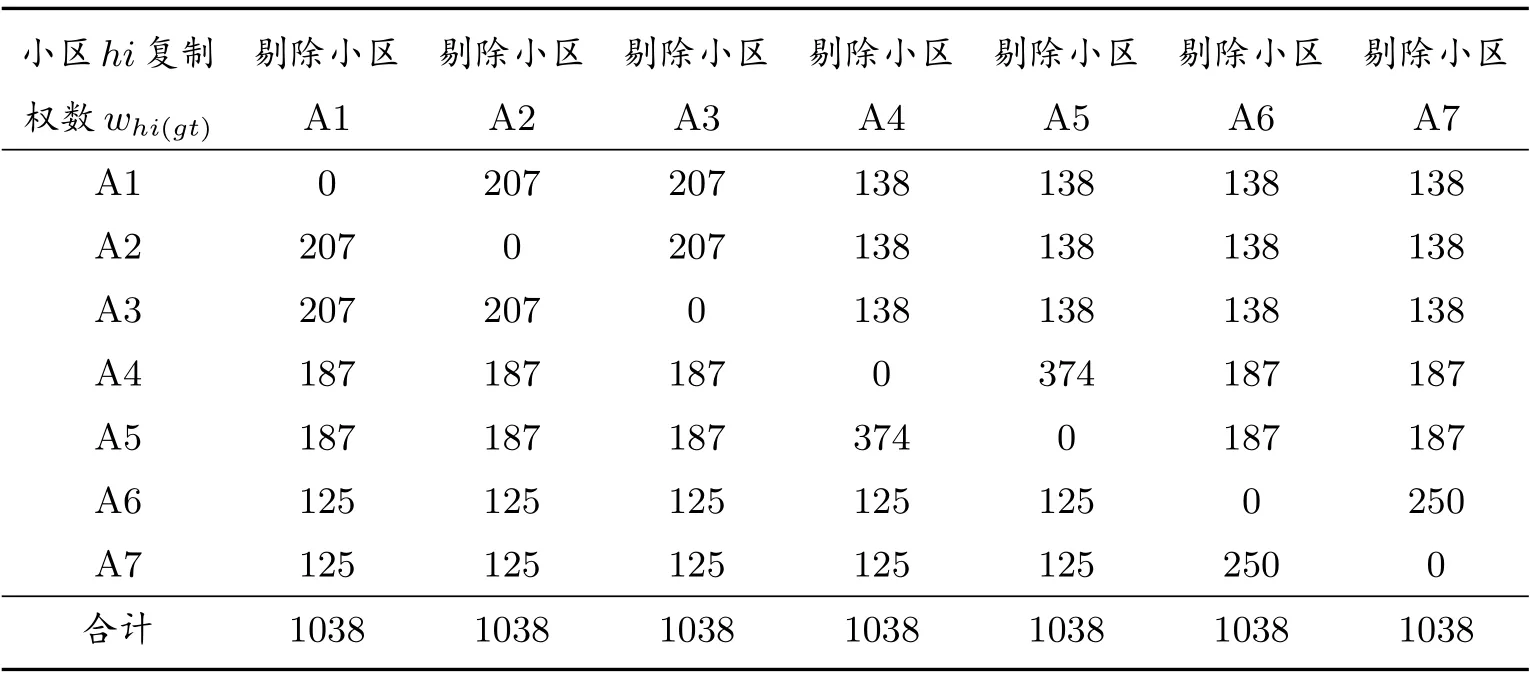
表8 样本普查小区的复制权数

从表8 可以看出，无论剔除哪一个样本普查小区，所有样本普查小区的复制权数之和与未剔除任何小区的所有样本小区的抽样权数之和相等.这说明，剔除某个样本小区后，总权数不变，但有些样本小区的权数变大，也有的样本小区权数变小，还有的小区权数不变.利用这些规律可以验证复制权数的计算是否正确.复制权数功能有三个.一是计算式(11)和(12)，以及式(15)和(16)每一个估计量的复制值.二是计算普查漏报复制估计值.三是计算普查漏报估计值的抽样方差.

表9 等概率人口层在三份名单的复制加权人数(人)(剔除t=A1)

表10 普查漏报复制人数(人)(剔除t=A1)

表11 普查漏报及复制漏报人数(人)

表12 抽样误差与协方差

表12 括号里面的数据为抽样标准误差.从表12 可以看出，采用质量评估调查-A，男性、女性和总体的抽样标准误差分别为352 人、272 人和171 人，即所估计的男性、女性和总体的普查漏报人数5107 人、6339 人和11446 人，与实际的男性、女性和总体的普查漏报人数平均相差352 人、272 人和171 人.采用质量评估调查-B，除女性外，男性和总体的抽样标准误差大一些.这说明，质量评估调查的人口构造方法对普查漏报估计的精度有影响.质量评估调查-A 使男性层和女性层呈负相关关系，协方差为负84238，降低普查漏报估计值的抽样误差，而质量评估调查-B 使男性层和女性层呈正相关关系，增加总体普查漏报估计值的抽样误差.因此，在普查漏报估计中，质量评估调查-A 提供精度更高的漏报估计值.

5.2 基于未匹配估计量的估计结果及数据分析

未匹配估计量，需要的样本资料是普查人口名单、质量评估调查人口名单及其匹配人口名单，以及样本普查小区的抽样权数.样本资料见表13 和表14.

使用表13 和表14 样本数据，按照式(31)和(32)，以及式(33)-(36)，我们得到总体普查漏报估计值及抽样方差.其中，质量评估调查-A 下的普查漏报估计值及抽样标准误差分别为9956 人和679 人，而质量评估调查-B 下的普查漏报估计值及抽样标准误差分别为8304 人和822 人.

表14 质量评估调查-B 样本普查小区人口资料(人)

5.3 普查漏报合成估计量与未匹配估计量的抽样方差数据比较

在对比普查漏报合成估计量与未匹配估计量估计精度之前，首先把它们估计的结果列示在表15 中，然后根据表15 进行数据对比分析.

表15 两种估计量的估计值(人)

在表15 中，从两种普查漏报估计量的比对来看：采用质量评估调查-A，普查漏报合成估计量提供的漏报人数及抽样标准误差的估计值分别为11446 人和171 人，而未匹配估计量给出的相应估计值分别为9956 人和679 人；使用质量评估调查-B，普查漏报合成估计量提供的漏报人数及其抽样标准误差估计值分别为9184 人和566 人，而依据未匹配估计量得到的估计值分别为8304 人和822 人.这表明，一方面，不论采用质量评估调查-A，还是质量评估调查-B，普查漏报合成估计量的漏报估计值都大于未匹配估计量给出的漏报估计值.这与后者未包括同时被普查名单和质量评估调查名单遗漏的人口，而前者包括同时被三份名单漏报的人口有直接关系.这也是提出普查漏报合成估计量的原因之一；另一方面，在质量评估调查-A 和-B 两种情况下，未匹配估计量的抽样方差大于普查漏报合成估计量，说明后者的有效性强于前者.从对比质量评估调查-A 或-B 来看：无论是普查漏报合成估计量，还是未匹配估计量，采用质量评估调查-A，所得到的抽样标准误差估计值，比质量评估调查-B 的都要小一些.

6 结论与建议

第一，相比普查净误差估计及普查多报估计，普查漏报估计尚未受到各国政府统计部门及相关学者应有的重视.建议政府统计部门将净误差估计、多报估计及漏报估计放在同等重要的位置，加强漏报估计基础理论研究，提高普查漏报估计精度.

第二，在判断质量评估调查-A 还是B 哪个更优时，要同时考虑三个因素：是否对普查标准时点人口的追溯登记；资料的可得性；抽样方差大小.质量评估调查-A 是对普查时点的追溯登记，符合人口普查质量评估的目标，抽样方差较小，但获取向外移动人口是否在普查时点登记有困难.只有在找到向外移动人口较容易的情况下，质量评估调查-A 才优于质量评估调查-B.建议政府统计部门在构造人口移动普查漏报合成估计量时，谨慎选择质量评估调查-A 或B.

第三，现行普查漏报估计方法存在覆盖漏报不全等缺陷.普查漏报合成估计量能够规避这些缺陷.该估计量需要在等概率人口层建立.这需要确定对总体人口分层的变量.在每一层，先构造全面登记的普查漏报合成估计量，再依据有限总体概率样本数据构造抽样登记的普查漏报合成估计量.汇总所有等概率人口层的普查漏报合成估计量，得到省、自治区、直辖市以及全国的普查漏报合成估计量.建议政府统计部门在2020 年前后使用普查漏报合成估计量；研究三份名单不同统计关系的缺失单元漏报估计量；加强对总体人口分层变量选择的研究，根据样本规模确定最终分层变量及其数目和等概率人口层的层数，尽可能减少普查漏报估计值的抽样误差.

第四，普查漏报估计量替代现行普查漏报估计量是必然趋势.首先，它包括了总体全部普查漏报人口.其次，它不受普查人口名单、质量评估调查人口名单和行政记录人口名单是否独立的限制.再次，它理论前沿.然而这种替代需要时间.建议政府统计部门与高校学者合作开展人口普查质量评估研究，尤其是前沿理论研究.