可见-近红外光谱原位估测土壤有机质含量中测试点和采样位置导致的误差分析

张昊丹，孙孝林, 2*，王晓晴，王会利

1. 中山大学地理科学与规划学院，广东省城市化与地理环境空间模拟重点实验室，广东 广州 510275 2. 土壤与农业可持续发展国家重点实验室(中国科学院南京土壤研究所)，江苏 南京 210008 3. 广西壮族自治区林业科学研究院，广西 南宁 530002

引 言

土壤是一种复杂综合体，其反射光谱是由其组成成分及结构等多种内在性质共同决定的结果[1-3]。因此，土壤光谱作为土壤理化性状的综合指标，在研究中常用于估测土壤属性，特别是可见-近红外(visible-near infrared, Vis-NIR)光谱。与传统化学分析土壤属性相比，室内测定土壤光谱虽已大大提高了效率，但仍需对样品进行预处理(如风干、研磨、过筛等)。相较之下，原位测定土壤光谱的效率更高，还具有快速、无损、可多次重复等优点。因此，越来越多的研究致力于发展原位土壤光谱估测土壤属性的技术，并取得了一定进展。例如，Viscarra Rossel等[4]、Li等[5]使用原位土壤Vis-NIR光谱估测土壤颜色、矿物组成、粘粒含量和有机碳。

这些研究也指出，利用原位土壤光谱估测土壤属性的准确性受诸多因素影响，包括两方面。一是土壤方面，主要是土壤非均质性所导致的水分条件、粒径差异、质地条件等；二是光谱测定方面，主要有光谱分辨率、测量时的外部环境、几何条件、土样表面处理方法、光谱处理技术等。前一方面的影响因素与室内测定土壤光谱影响因素的研究结果都较一致。史舟等[1]已对此做了比较全面、系统的总结。后一方面的因素在很多光谱估测土壤属性的研究中得到了深入分析。例如，刘焕军等研究了光谱分辨率对黑土有机质预测模型的影响, 结果表明：黑土有机质含量高，土壤有机质的光谱范围宽(445～1 380 nm)，且光谱预测模型精度随光谱分辨率降低呈先增后减的趋势，最优模型的光谱分辨率为50 nm；侯燕平等[7]研究了土样表面处理方法对光谱测定的影响，具体表现为表面刮平处理方式优于压平与摇平处理方式；Stenberg[8]研究了实验室内土壤样品预处理和标准化复湿对Vis-NIR光谱预测粘粒和土壤有机碳的影响，发现将土壤样品重新润湿到体积标准化水平可显著提高土壤有机碳的估测效果，粘粒含量估测效果也有改进但不如前者明显。

为了削弱土壤的非均质性对原位土壤光谱估测土壤属性的准确性的影响，原位土壤光谱的测定一般是多点测定后取平均值，再用于土壤属性估测。如Morgan等[9]在土芯上每隔2.5 cm各测定4个位置的光谱，并取平均值用于估测有机碳和无机碳；Lobsey和Viscarra Rossel[10]测定了每个环刀土样两面各5个位置的光谱并取平均值用于土壤水分估测；Li等[5]测定了环刀样品上5个随机位置的光谱后取平均值，用于土壤有机碳分析。此外，广泛的土壤学研究中，一般对同一层的土壤，如土壤发生层或同一深度层，选取多个位置的样品充分混合。因此，同一层的不同采样位置也会影响原位土壤光谱估测土壤属性的准确性。然而，迄今的大量研究主要集中在数据预处理与预测模型方面[11]，鲜有研究分析原位土壤光谱测试点位置以及同一土层不同采样位置对土壤属性估测的影响。因此，这两个因素导致的光谱差异及土壤属性估测误差还不清楚。

为此，以我国南方典型丘陵区林地上的土壤样品为例，首先分析同一原状土样品不同测试点位置上以及同一土层不同采样位置上的光谱差异，再按照原位土壤光谱估测土壤属性的一般模式，用偏最小二乘回归(partial least square regression, PLSR)方法建立样品的平均光谱与有机质含量之间的模型，接着使用该模型估测不同光谱测试点位置和采样位置上的有机质含量，从而评价测试点和采样点位置不同导致的有机质含量估测误差。研究目的在于定量揭示光谱测试点位置、土壤采样点位置的不同导致的土壤属性估测误差，为后续进一步研究如何降低这些误差指明方向，有助于未来更好地开展原位土壤光谱估测土壤属性的研究和应用。

1 实验部分

1.1 研究区概况

研究区选在广西壮族自治区南宁市北郊丘陵地带的高峰林场(108°20′57″—108°21′54″E ，22°57′8″N—22°58′41″N)，面积约3.03 km2，高程约120～300 m。该研究区位于南亚热带湿润季风气候区，年均温为21.6 ℃，年降雨量1 304.2 mm；土壤母质主要为泥岩、泥质页岩、砂质页岩等沉积岩系，均风化发育为赤红壤；植被以人工桉树林为主，林下灌草植物以木姜(Litseapungens)、毛桐(Mallotusbarbatus)、盐肤木(Rhuschinenesis)、半边旗(Pterissemipinnata)、五节芒(Miscanthusfloridulus)、铁芒箕(Dicranopterisdichotoma)等为优势树种。该研究区历史上一直为林地，21世纪初开始种植桉树[12]。

1.2 土壤采样

从研究区的数字高程模型中提取出高程、坡向、坡度、剖面曲率、平面曲率和地形湿度指数，并在这些地形参数的基础上，采用条件拉丁超立方方法选取了20个不同地形特征的采样点。在这些采样点位置上，挖掘土壤剖面，深至母质层，当母质层深度超过140 cm时深至140 cm。每个剖面划分发生层后，用环刀在每层的不同位置重复采样2个，共采集160个环刀样品。另外，在该研究区内用网格法选取38个样点，每个样点重复采集表层不同位置上的环刀样2个，共采集76个环刀样品。因此，共采集236个环刀样品。

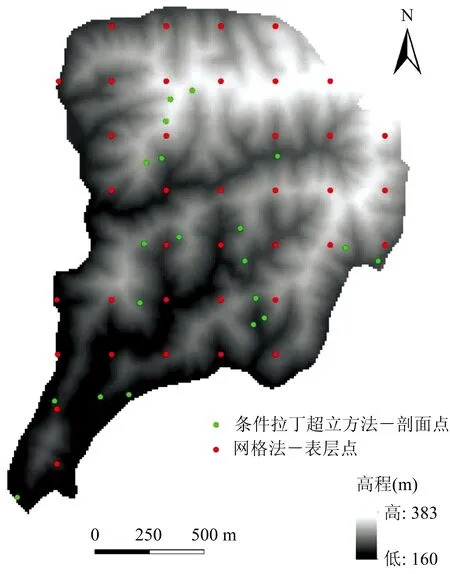
图1 研究区内采样点分布Fig.1 Distribution of sampling points in the study area

1.3 土壤测试

原状土壤光谱由美国ASD公司生产的FieldSpec4型便携式高分辨率地物光谱仪在室内测得，测量光源为杯状光源，内置12°天顶角的卤素灯，配有接触式光纤探头。该仪器波长范围是350～2 500 nm，350～1 000 nm内采样间隔为1.4 nm，1 001～2 500 nm内采样间隔为1.1 nm，光谱分辨率为3 nm@700 nm，6 nm@1 400/2 100nm，输出总波段数是2 151。测量时，将杯状光源置于环刀土壤样品上方，光纤探头直接接触样品。每个样品的上、下两面分别均匀选取9个点进行测量，每个点测得10条光谱。由于光谱在起始波段(350～400 nm)和长波近红外波段(2 451～2 500 nm)受杂散光、样品背景、测量仪器系统等因素的影响而混有噪声，故本文用401～2 450 nm波段范围的光谱数据进行下一步分析[5]。同时，为避免因数据冗余出现过度拟合现象，参考Shepherd[13]和Stenberg[8]的研究，分别以5和10 nm采样间隔对401～1 000和1 001～2 450 nm两个波段进行重采样，共输出265个波段。

光谱测定后的环刀样品经过风干、研磨等一系列处理后，用重铬酸钾容量法测得有机质含量。

1.4 土壤光谱曲线之间的差异计算

不同的光谱曲线具有不同的形状和幅度。本文用光谱角度θ[1]来评价它们之间的差异性，计算公式如式(1)

(1)

式(1)中，xi和yi分别为两个光谱曲线x和y在波段i处对应的反射率值，n表示波段数。θ值越小，表明曲线x和y之间的差异越小，反之则差异越大。

为消除仪器因素引起的误差，以每个测试点10条光谱的平均作为该测试点的光谱，并称为测试点光谱(共4 248条)，以便区分其他光谱。进一步地，计算每个环刀样品上、下两面共18个测试点光谱的平均值，称为环刀样光谱(共236条)；计算每个土层两个环刀样品共36个测试点光谱的平均值，称为土层光谱(共118条)。然后，计算每个环刀样品18个测试点光谱与对应环刀样光谱之间的光谱角度，以评价光谱测试点位置不同引起的光谱测定差异。相似地，计算每个土层2个环刀样光谱与对应土层光谱之间的光谱角度，以评价采样位置不同引起的光谱测定差异。

1.5 土壤光谱估测土壤属性的模型建立与验证

使用PLSR建立土壤光谱与土壤属性之间的模型。PLSR在土壤近地传感研究中应用最广泛，应用效果良好[3-5]。为避免过度拟合PLSR模型，使用留一交叉验证法(leave-one-out cross validation，LOOCV)选择最合适的潜变量(latent variable, LV)个数来建立PLSR模型。然后，再采用随机独立样本对模型进行验证：全部样本(236个)被随机分为建模集和验证集。为避免样本数不同给验证结果带来的影响，验证集的样本数取值为1～40，取剩后的样本全部用于建模。同时，为了降低随机采样的不均匀性对验证结果的影响，对每个验证集样本数重复进行了100次，并取100次的平均结果为该模型的验证结果。验证指标包括：平均偏差(mean error，ME)、均方根误差(root mean square error，RMSE)、决定系数R2和相对分析误差(residual prediction deviation，RPD)，计算公式如式(2)—式(5)

(2)

(3)

(4)

(5)

1.6 误差分析

将每个环刀样品的18条测试点光谱输入到PLSR模型中，得到18个有机质含量估测值。在此基础上，计算这些估测值的平均值、标准偏差和变异系数。用其中的标准偏差表示因测试点位置不同导致的光谱估测土壤有机质的误差。

同样的，将每个土层的2条环刀样光谱输入到PLSR模型中，得到2个有机质含量估测值，接着计算这些估测值的平均值、标准偏差和变异系数，并用其中的标准偏差表示因采样位置不同而导致的光谱估测土壤有机质的误差。

2 结果与讨论

2.1 采样土壤的有机质含量统计特征

表1列出了采样获得的土壤有机质含量的统计特征。所有236个环刀样的土壤有机质含量的变异性较大，变异系数达61%，属中等变异。偏度与峰度值说明样品有机质含量呈向右偏离正态分布，且峰态平缓。

表1同时还列出了每个土层2个重复样的土壤有机质含量统计特征；图2展示了它们之间的对比。表1中的结果表明，重复样本之间的统计特征差别很小，且都接近所有环刀样的统计特征。例如，两次重复的均值分别为20.68和19.81 g·kg-1，标准偏差分别为12.23和12.51 g·kg-1，与所有环刀样本的均值20.25 g·kg-1和标准差12.36 g·kg-1都很接近。由图2可见，当有机质含量低于25 g·kg-1时，每个土层的两次重复实测有机质含量接近1∶1线，而当有机质含量高于25 g·kg-1时，两次重复与1∶1线有一定程度的偏离。这种偏离说明，高有机质含量的土层中，土壤有机质在层内分布不均匀，例如有机质含量丰富的土壤表层过渡到有机质含量较低的下层时，有机质含量并不均匀，而是快速或慢速降低。这一结果说明研究土壤采样位置不同导致的误差具有重要意义。

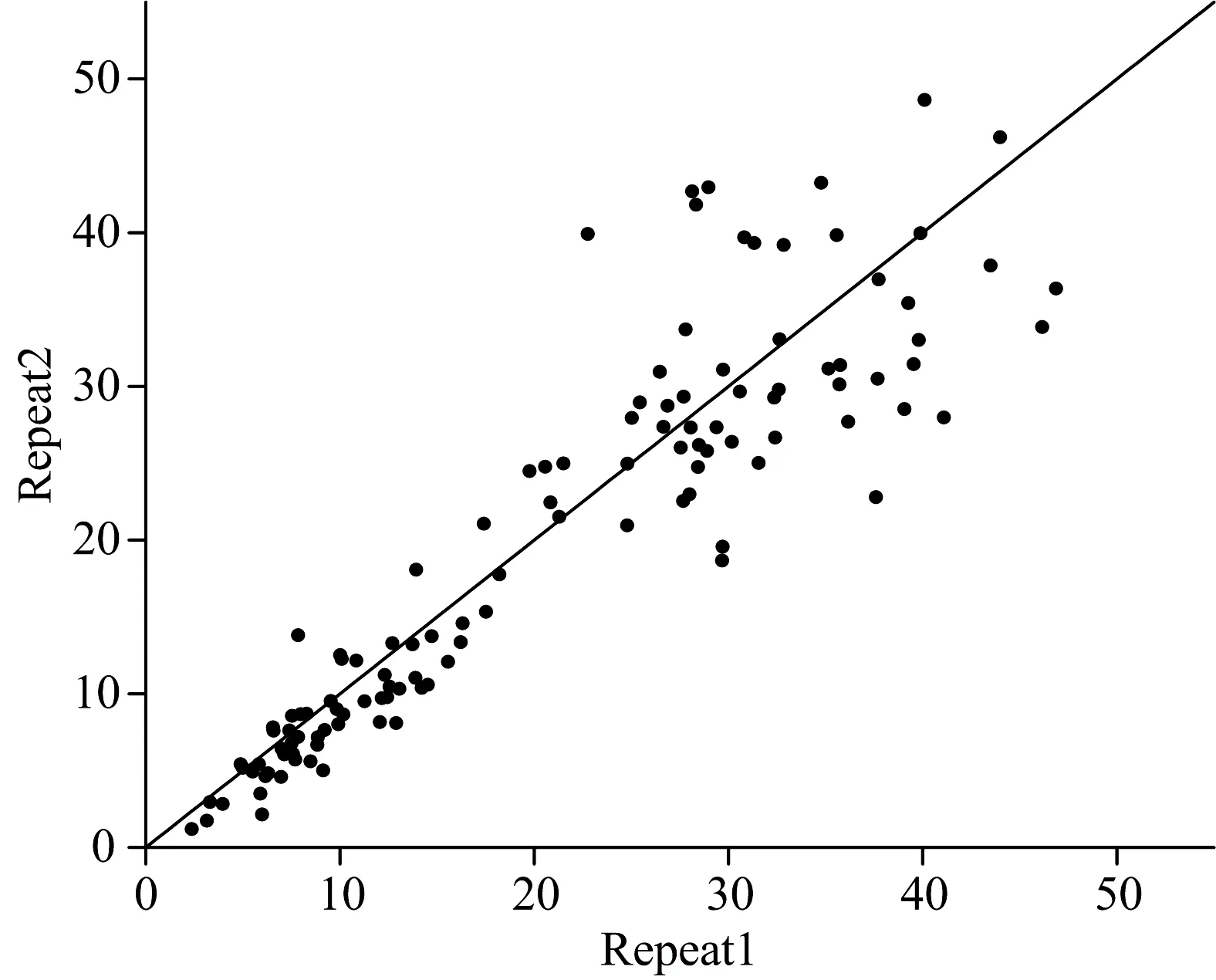
图2 两次重复环刀样的土壤有机质含量测量值对比Fig.2 Comparison of soil organic matter contents of two duplicate sets of samples

表1 土壤有机质含量(g·kg-1)的统计特征Table 1 Statistics of soil organic matter content(g·kg-1)

此外，表1还列出了每个土层的有机质含量，即该土层2个重复样的平均值的统计特征。可见，土层的有机质含量统计特征与上述所有环刀样及2个重复样中有机质含量的统计特征基本一致。

2.2 光谱曲线之间的差异分析

本文以所有样品中有机质含量最低(1.20 g·kg-1)、最高(48.64 g·kg-1)和最接近平均值(20.57 g·kg-1)所对应土层的样品为例，展示本研究测得的光谱，如图3所示。由于有机质含量的较大差异，图3(a)，(b)和(c)中的光谱反射率差异较大，表现为有机质含量越高的土壤，其反射率低[6]。不同环刀样品的光谱在700～1 000 nm范围内有明显的波形差异，尤其是图3(a)中900 nm附近可见明显吸收谷。因690～930 nm波段为铁的氧化矿物对光谱的主要吸收区[16]，故该波段反射光谱主要受土壤有机质和氧化铁的共同影响。本研究采集的土壤类型为赤红壤，含丰富的氧化铁，尤其是有机质含量少的下层土壤中。因此，在图3(a)中表现出了900 nm附近的明显吸收谷。

在图3中，灰色和浅绿色分别表示同一土层2个环刀样品各18条测试点光谱(共36条)；蓝色表示2个环刀样光谱；红色表示土层光谱。可以看到，同一环刀样品上不同测试点位置处的测试点光谱(图3中灰色和浅绿色曲线)在形态上大体一致，但在不同的波段上，反射率值存在着不同程度的差异。较大的差异发生在600～1 350，1 400～1 850和1 900～2 500 nm三个波段范围内。在1 400，1 900和2 200 nm三个波段附近光谱曲线差异较小，分别对应于水分吸收特征明显的波段[3, 15]。

图3还反映出同一土层不同取样位置之间，即环刀样光谱(图3中蓝色曲线)之间，也存在着一定程度的光谱差异，并与土层光谱(图3中红色曲线)有一定差异。这些差异与上述测试点光谱之间的差异相比非常小。

表2列出了测试点光谱与环刀样光谱之间、环刀样光谱与土层光谱之间角度的统计特征。偏度值和峰度值说明两组角度的分布比较相近，均向右偏离正态分布，峰态陡峭。前者的均值、最大值、中值都大于后者，说明测试点光谱与环刀样光谱之间的差异大于后者。这一结果表明，土壤光谱测试点不同导致的光谱差异远远大于采样位置不同导致的光谱差异。前者比后者大约76%。这可能是因为每一个土壤样品的18个光谱测试点分布在环刀样品的上、下两面(每个面各9个点，而环刀深度为5 cm，即上下两面相距5 cm)，因而测试点位置实际上已包含了采样位置不同引起的差异。同时，环刀样光谱是测试点光谱的平均值，因而已消除了部分差异，使得环刀样光谱之间差异缩小。另外，环刀样光谱之间的差异较小也可能与样本数有关，本文中每个土层仅有2个环刀样光谱。

表2 光谱曲线与参考谱线之间的角度差异统计特征(单位：度)Table 2 Statistics of differences in degree between the sample spectrum and reference spectrum

图4列出了土壤光谱之间的角度与环刀样有机质含量之间的对比关系。该图反映出，光谱之间的角度与有机质含量无明显的相关关系。进一步的相关性分析表明，测试点光谱与环刀样光谱之间的角度与有机质含量的最大负相关和正相关分别为-0.061和0.079，最小负相关和最小正相关分别为-0.028和0.008。环刀样光谱与土层光谱之间的角度与有机质含量之间的相关性系数为-0.02。可见，这些相关性并未达到统计学上的显著性水平，说明它们之间的相关性不明显。

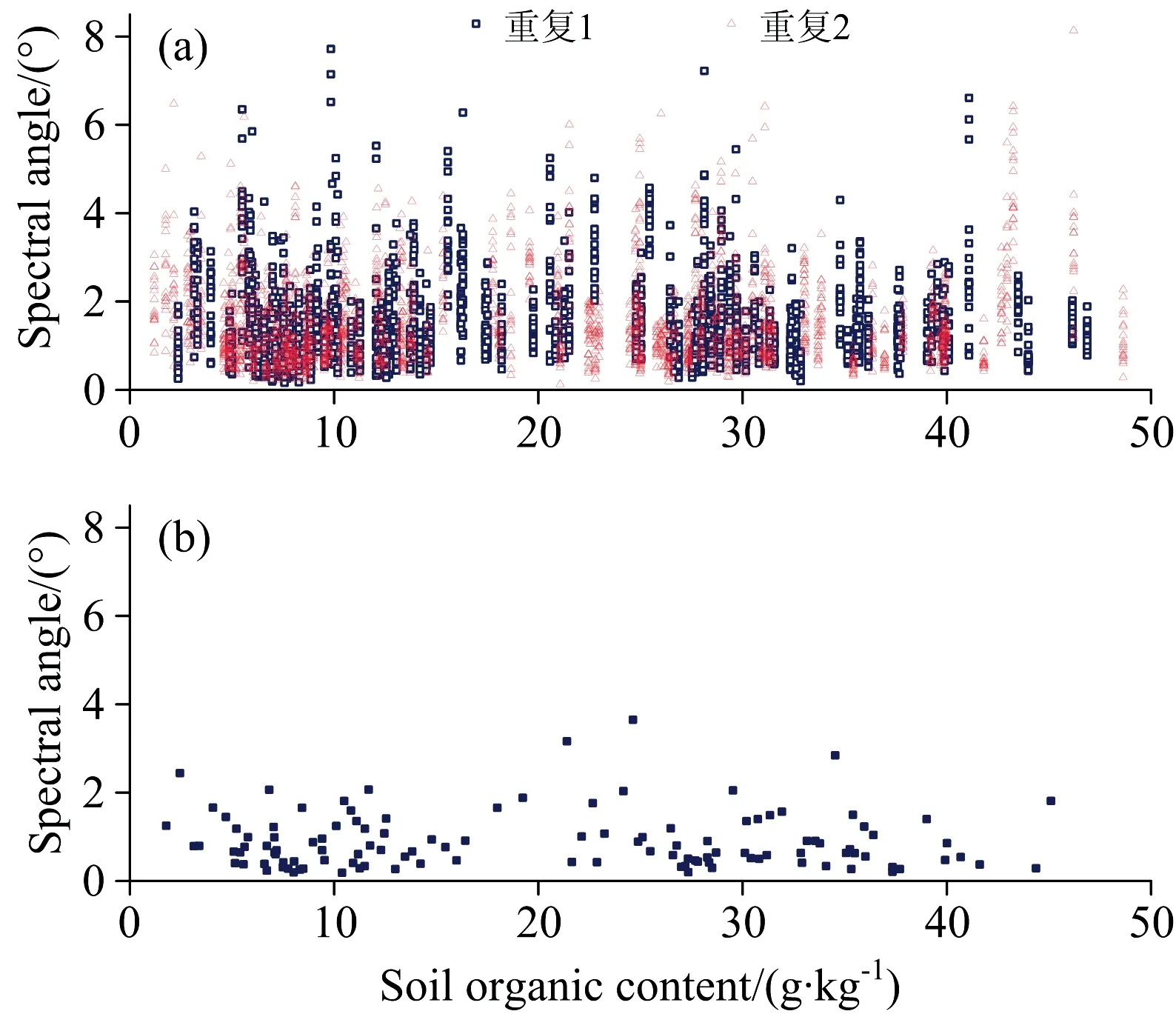
图4 土壤有机质含量与土壤光谱差异(a)：测试点光谱与环刀样光谱间的角度；(b)：环刀样光谱与土层光谱间的角度Fig.4 Soil organic matter content and the differences between soil spectra

2.3 土壤原位光谱估测有机质含量的PLSR模型与验证

用所有(236个)环刀样光谱和有机质含量建立PLSR模型。图5显示了这些光谱与有机质含量之间的相关性。可见，在大部分波段上，光谱反射率与土壤有机质含量之间呈现负相关，最大负相关系数为-0.918，对应波长为1 215.5 nm；只在极小波段范围内(2 196～2 226，2 326～2 406 nm)呈正相关，最大正相关系数为0.163，对应波长为2 205.5 nm。这一结果与Shepherd[13]的研究结果相似，说明可以合理地利用光谱建立估测有机质含量的PLSR模型。

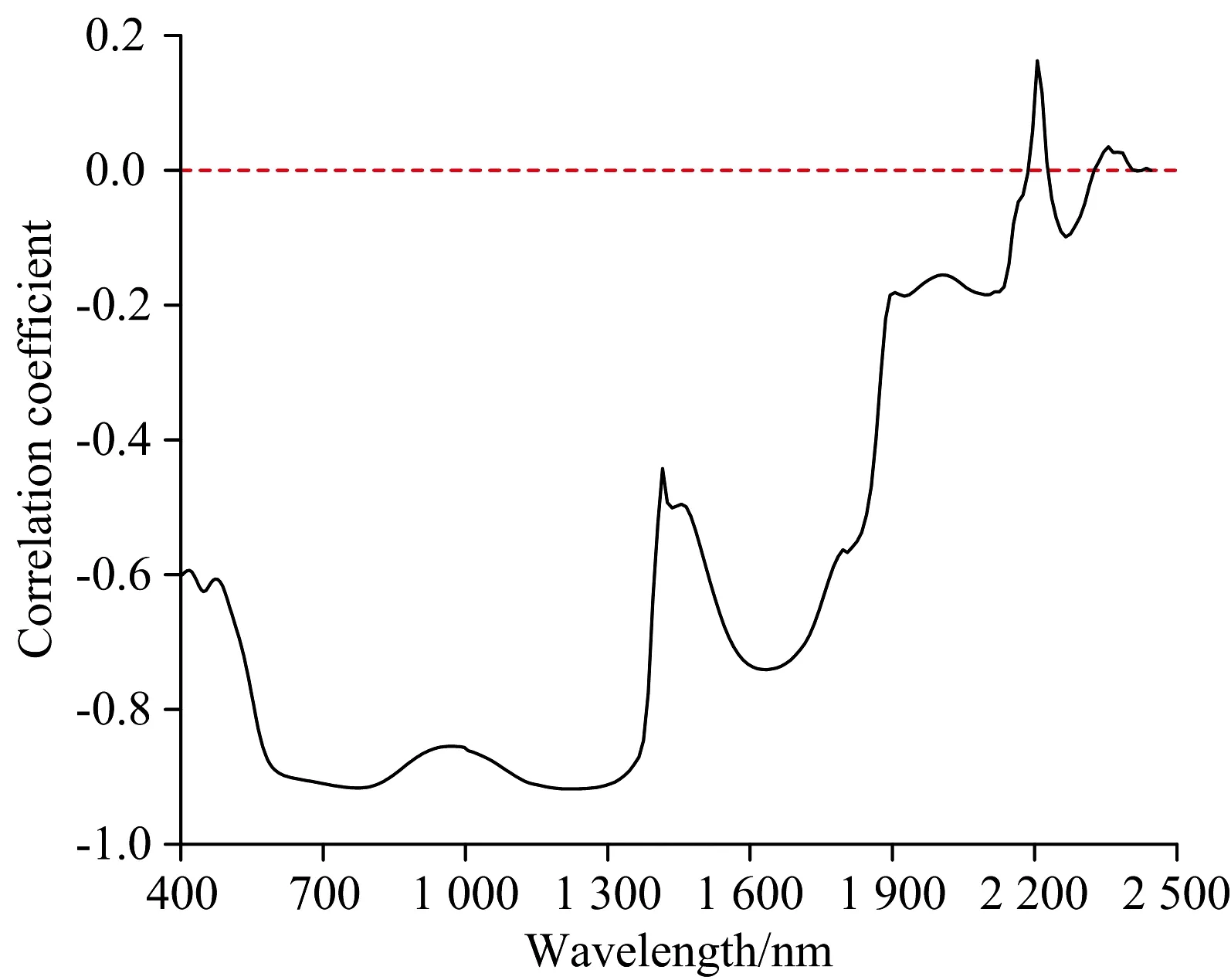
图5 土壤有机质含量与环刀样光谱反射率的相关性分析Fig.5 Correlogram of soil organic matter content to spectral reflectance of each sample

使用一系列不同潜变量个数的PLSR建模和LOOCV验证的结果(图6)表明：当潜变量个数小于23时，估测值的误差平方和呈现总体下降趋势，仅在个别潜变量个数上略有微小增加的趋势；当潜变量个数为23时，估测值的误差平方和达到最低；当潜变量个数大于23时，估测值的误差平方和有微小增加，但并没有太大改变，趋于平稳。因此，使用潜变量个数为23来建立PLSR模型。LOOCV的结果表明，该模型的ME是-0.002 6 g·kg-1，RMSE是3.57 g·kg-1，分别占表1中所有样本有机质含量平均值的-0.013%和18%。其中，RMSE的结果说明该模型具有一定误差。该模型的决定系数R2是0.92，RPD是3.46，与其他研究中的R2和RPD接近[3, 5]。尤其是RPD的结果，说明该模型的预测能力极佳。

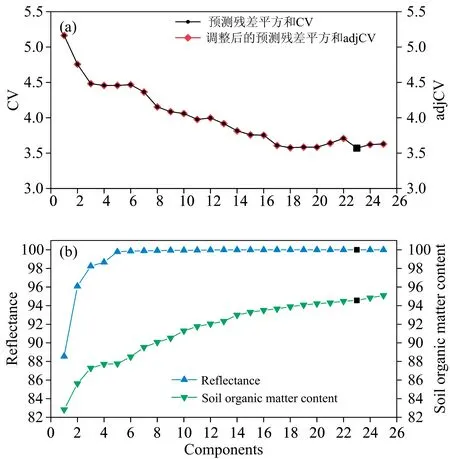
图6 PLSR模拟结果

接着用随机抽取的1～40个样本对该模型进行了验证，每个随机抽取样本数重复100次并取其平均值作为验证结果。如图7所示，当随机抽取的样本数大于3时，验证指标值趋于稳定。而且，由于样本数较小时很可能出现较大偏差而使得评价结果失真，例如图7(c)中R2值在样本数为1时其值为1，显然是因为样本数仅为1造成的。因此，以随机抽取的样本数大于3时的结果来评价模型的准确性。ME在-0.52～0.34 g·kg-1之间，占表1中所有样本平均值的-2.57%～1.68%，可见总体误差非常小。然而，这可能是因为正、负误差相互抵消的原因。相对应地，图7(b)中的RMSE相对较高，在3.15～3.70 g·kg-1之间，占表1中所有样本平均值的16%～18%。这一结果说明该模型具有一定的误差。图7(c)中的决定系数R2在0.91～0.93之间，高于Li等统计文献中曾报道的0.68～0.92之间。同时，RPD在3.38～4.38之间。这些结果说明，该模型具有较高的准确性。

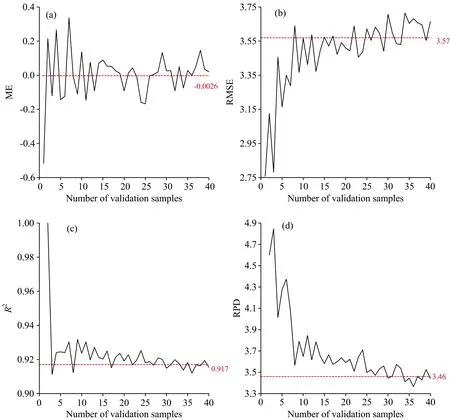
图7 PLSR预测模型的独立随机样本验证结果统计分析

2.4 测试点和采样位置导致的误差分析

图8展示了光谱估测的有机质含量及其平均值、标准偏差与实测有机质含量的对比关系。从图8(a)中可以看到，不同的测试点位置，估测值有较大的变异，说明测试点位置不同导致的误差比较大。用标准偏差表示该误差的结果也展示在图8(a)中，即蓝色点。进一步分析表明，该标准偏差与有机质含量实测值的相关系数为0.23，达到了0.01水平上的显著性。这说明，实测值越大，标准偏差越大。同时，表4列出了该标准偏差的统计数据。可以看到，该标准偏差的平均值、最小值和最大值分别占表1中所有样品有机质含量平均值的17.98%，4.54%和72.40%。可见，测试点位置不同导致的误差并不小。鉴于前述标准偏差与实测有机质含量有显著的相关性，进一步分析了标准偏差占对应有机质含量实测值的百分数，统计结果也列于表4中。可以看到，测试点位置不同导致的标准偏差占实测值的百分数平均可达31%，最小值为3.8%，而最大值可达428%。可见，该标准偏差比2.3节中模型的误差还要大(在2.3节中，模型的RMSE占样品有机质含量平均值的16～18%)。

在分析采样位置导致的误差中，取每个土层两个环刀样实测有机质含量的平均值作为该土层有机质含量的实测值。图8(b)表明，同一土层上环刀采样位置的不同也会导致明显不同的估测值，说明采样位置不同导致的误差比较明显[图8(b)中的蓝色点]。进一步的相关性分析表明，用标准偏差表示的该误差与土层有机质实测值的相关系数为0.30，达到了0.01水平上的显著性。因此，采样位置不同产生的标准偏差也会随着实测值的增大而增加。表4列出了该标准偏差的统计特征。可见，该标准偏差的平均值、最小值和最大值分别占表1中所有土层实测有机质含量平均值的11%，0.03%和57%。因此，由于采样位置不同导致的估测标准偏差也较大。进一步分析了该标准偏差占对应实测值的百分数，并将结果列于表4中。该结果表明，该标准偏差占实测值的百分数平均值为15%。可见，该标准偏差比2.3节中模型的误差要小(在2.3节中，模型的RMSE占样品有机质含量平均值的16%～18%)。

图8和表4的结果都表明，因测试点位置不同导致的标准偏差明显大于因采样位置不同导致的标准偏差。以表4中两者的平均值来看，前者比后者大约60%。这与前述土壤光谱差异有关。如前所述，测试点不同导致的光谱差异比采样位置不同导致的光谱差异大约76%。因此，在原位光谱估测土壤属性的研究中，更应该注意测试点位置不同导致的误差。迄今为止的文献大多采用多点测定和多样本采样取平均值来应对这两种误差，并未定量分析它们的大小。然而，尽管本文指明了这两种误差的大小，但仍然未能提出有效地降低它们的方法。未来，除了研究利用不同的模型来降低误差外，还需要研究更有效的方法来降低这些误差。

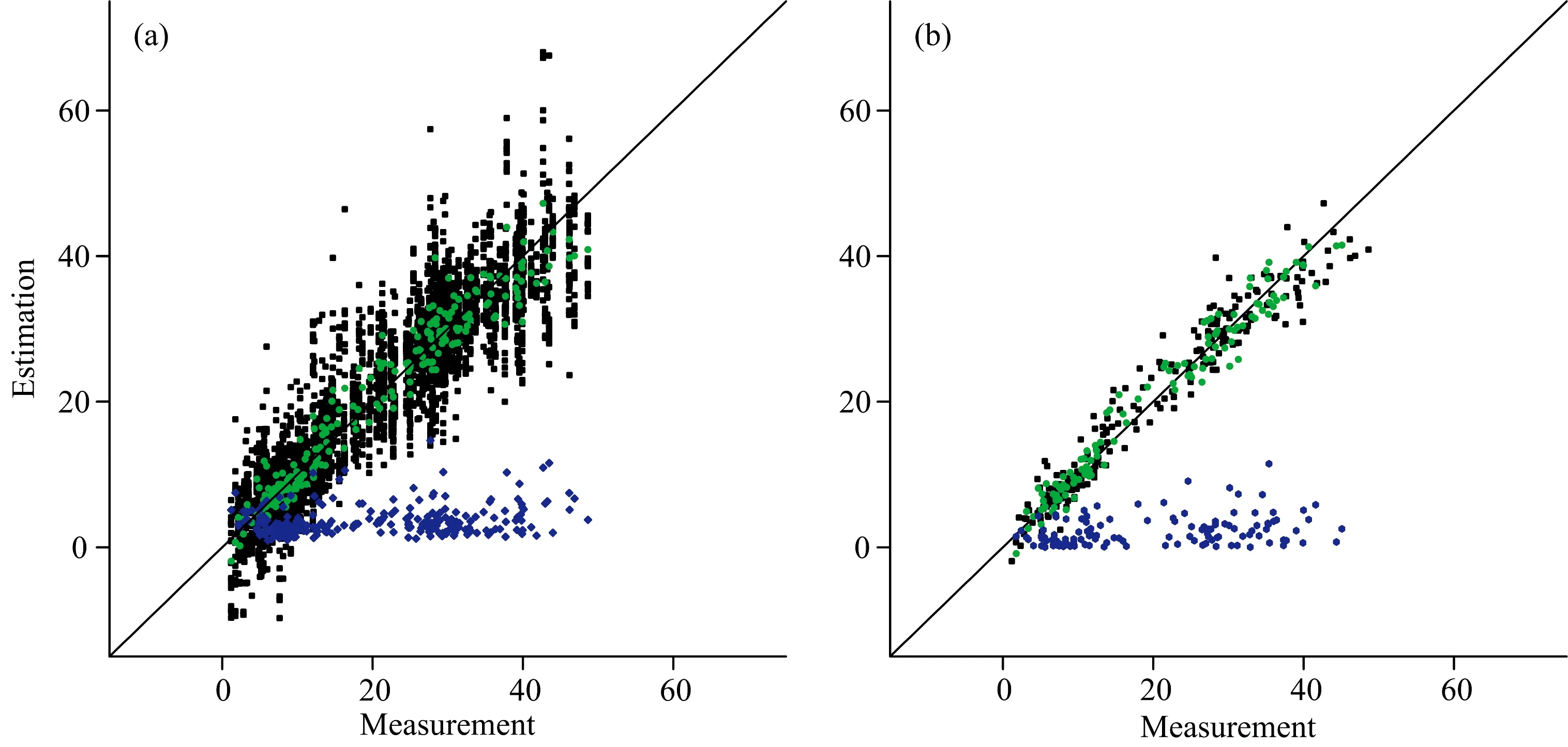
图8 测试点光谱(a)和环刀样光谱(b)估测的有机质含量(黑色)、平均值(绿色)及标准偏差(蓝色)与实测有机质含量的对比；在(b)中，光谱估测值与实测有机质含量进行对比，而其他值都与每个土层的两个环刀样的平均值进行对比

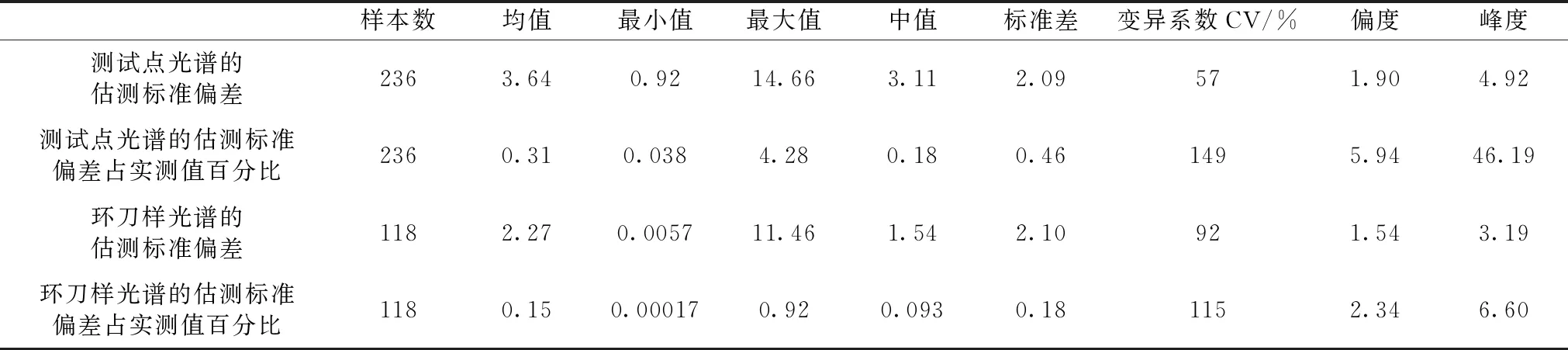
表4 原位土壤光谱估测有机质含量的误差(用标准偏差表示)的统计特征Table 4 Statistics of the error of soil organic matter content estimated by in situ soil spectra (by standard deviation)

3 结 论

以我国南方典型丘陵区林地中的土壤样品为例，定量分析了光谱测试点和采样位置不同导致原位土壤光谱估测有机质含量中的误差。结果表明，光谱测试点不同导致的土壤光谱差异平均为1.55°，而采样位置不同导致的土壤光谱差异则相对较小，平均为0.88°。两种差异导致光谱估测土壤有机质的误差平均值分别为3.64和2.27 g·kg-1，分别占对应实测值的31%和15%。并且，前者大于 PLSR模型导致的误差。结果表明，测试点和采样位置不同导致原位光谱估测土壤属性的误差较大，在今后的研究中应当注意它们的影响。未来研究还需要探讨如何降低这些误差，提高原位光谱估测土壤属性的准确性。