花岗岩硬性结构面剪切强度特性模型试验研究

赖冠宙，黄 帆，温辉波

(1.广东大潮高速公路有限公司，广东 梅州 514000；2.招商局重庆交通科研设计院有限公司，重庆 400067)

花岗岩类岩质边坡失稳滑动区别于土质斜坡变形的一个明显特征就是前者往往具有一个或多个相对明确的滑动面(带)，该滑动面大多为岩体的地质分离面，即岩体结构面，边坡发生失稳变形时，滑体则主要依附此分离面运动[1-2]。因此，从某种意义上说，岩质边坡失稳的变形破坏机理就是结构面所构成的潜在滑动带的变形破坏机理。岩体工程实践表明，只要岩体中存在不利结构面构成的软弱地质界面或分割面，岩体就有可能沿着这些结构面发生变形破坏[3-6]。在边坡设计和稳定性评价时，较多依据各向同性介质理论，采用极限应力方法确定近似圆弧滑面，作为边坡稳定性计算和设计参数选择的依据[7-9]。然而大量的滑坡实例分析和试验结果表明，对于包含强度明显弱于岩体强度软弱层面的层状边坡，发生圆弧滑动的概率是极小的，实际失稳多为受结构面控制的结构体滑坡，多以平面滑动为主[10]。因此，从另外一个角度来讲，对于内部含一组或多组层状缓倾结构面的岩质高边坡，内部结构面往往对其区域稳定性或整体稳定性起控制作用，岩体自身强度则影响较小[11]。

本文通过对花岗岩硬性结构面开展大型直剪模拟试验，并从抗剪强度中剪胀分量和摩擦分量2部分及其在抗剪切过程中各自所发挥的作用进行考虑，对岩体结构面抗剪切强度特性进行分析。

1 试验方案设计

本次试验所用剪切盒尺寸为20 cm×20 cm×10 cm，试验对无填充花岗岩硬性结构面的抗剪力学特性分别开展研究，因此在试验材料制备时，按照岩体(结构体)选择相似材料进行制样。

1.1 试样制备

在对花岗岩相似材料进行制备时，在确保其法向加载后不被破坏的前提下，选择水泥砂浆按照水泥、砂、水质量比为1∶2∶0.4的比例进行试件配制后，制作好试验材料并进行养护，结构体试样基本力学参数如表1所示。

表1 结构体试样基本力学参数

1.2 界面起伏度设计

对于无填充或仅有极少泥膜粘结的花岗岩硬性结构面，结构面的起伏度对于其抗剪强度有较为显著的影响。抗剪强度测算方法采用Barton[12]提出的JRC-JCS模型，其表达式为：

(1)

式中：τp为峰值抗剪强度，MPa；σn为有效法向应力，MPa；φb为基本摩擦角，(°)；JCS为结构面两侧岩石的单轴抗压强度，MPa；JRC为粗糙度系数。

本文对所提出模型中JRC值进行量化处理，结构面采用齿状设计，通过设置不同的齿状受力面倾角来模拟不同的爬坡角，以此研究摩擦分量中剪胀分量对抗剪强度的影响。齿状结构面设计剪胀角为15°、30°、45°，制备得到的齿状结构面试样如图1所示。

(a)15°剪胀角

粗糙结构面的起伏程度通常分为2个级别：一阶突起是与结构面上主要起伏相对应的凸起，二阶凸起是结构面上相对较小的凸起。相对于一阶粗糙凸起，二阶粗糙凸起往往具有更大的爬坡角，但由于二阶凸起角度大，在一定的法向压力作用下，发生切向相对位移时极易被剪断，因此抗剪强度主要由一阶凸起控制。本文所讨论的结构面爬坡角也是指一阶凸起控制的爬坡角,而平直结构面的粗糙度主要由二阶凸起控制。根据结构面设计方案，参照Du[13]提出的JRC修正直边法多量程粗糙尺，对本次试样中结构面的粗糙度系数进行确定，15°、30°、45°三种爬坡角结构面的粗糙度系数分别为7.44、12.12、17.21。

2 花岗岩硬性结构面抗剪强度试验

在进行花岗岩硬性结构面抗剪强度分析时，不考虑结构面间粘聚力作用，假定结构面间抗剪强度由摩擦分量和剪胀分量组成，分别开展平直结构面及齿状结构面剪切试验研究。

2.1 平直结构面剪切试验过程分析

针对平直无填充花岗岩硬性结构面(剪胀角为0°)试样开展了轴压为0.5 MPa、1.0 MPa及1.5 MPa的直剪试验，试验采用应变控制式，剪切速率为5 mm/min，剪切距离为40 mm，剪切试验过程中对切向应力、位移及法向应力、位移数据进行实时监测，数据采样频率为3.9 Hz。

2.1.1 剪应力-剪切位移关系分析

选择平直结构面试样分选设置0.5 MPa、1.0 MPa和1.5 MPa三种不同轴压条件，分别开展大型直剪试验，得到其剪应力及剪切位移之间的关系曲线，如图2所示。

图2 平直结构面剪应力与剪切位移关系曲线

从图2可以看出，试样剪切开始后随着剪切位移的增加，结构面剪切应力不断增加。剪切应力峰值随轴压的增加不断增大，但在0.5 MPa及1.0 MPa轴压条件下，剪应力达到峰值后随即趋于恒定，且峰值应力与残余应力区分度不显著，而在1.5 MPa轴压条件下，花岗岩硬性结构面存在咬合剪断的情况，剪应力曲线达到峰值后回落至残余强度，3种工况应变变形曲线差别明显。

2.1.2 剪胀特性分析

为研究平直结构面的剪胀特性，针对平直结构面分别选择不同的轴压条件开展直剪试验，可得到不同工况下其法向位移与剪切位置之间的关系曲线，如图3所示。

图3 平直结构面法向位移与剪切位移关系曲线

从图3可以看出，整个剪切过程中，剪切试样表现出显著的剪胀特性。随着法向压力的增加，法向剪胀效果越来越明显，剪胀速率与最大剪胀量随着轴压的增加而不断增大，剪缩时间不断推后，不过3种轴压条件下剪缩速率大致相同，均为0.021 mm/min。

2.1.3 平直结构面峰值抗剪强度分析

1)考虑结构面间粘聚力作用

当考虑结构面间粘聚力作用时，选择3种轴压条件所对应的峰值强度进行平直结构面抗剪强度分析，如图4所示。

图4 平直结构面抗剪强度分析

通过对平直结构面分别开展0.5 MPa、1.0 MPa、1.5 MPa轴压条件的直剪试验，获得峰值剪切应力，对其进行回归分析，采用最小二乘法进行线性拟合，如图4所示，可得到平直结构面抗剪强度表达式：

τs=0.006 67+σ0.86

(2)

式中：τs为平直结构面抗剪强度，MPa；σ为结构面法向压力，MPa。由该拟合曲线斜率0.86可以得到平直结构面宏观摩擦角为40.7°，表观粘聚力为0.006 67 MPa，试验中得到的表观粘聚力认为是岩体间的一种咬合作用，是一种隐形的摩擦力，表现为宏观的粘聚力。

2)忽略结构面间粘聚力作用

由于该线性回归中得到的粘聚力数值较小，且无填充花岗岩硬性结构面抗剪强度分析时，可忽略裂隙岩体间粘聚作用，对试验中得到不同轴压下的峰值剪应力重新进行回归分析，同样采用最小二乘法线性拟合，并设定截距为0，即忽略粘聚力作用，可得到平直结构面抗剪强度曲线，如图5所示。

从图5可得到忽略粘聚力作用条件下的平直结构面抗剪强度表达式为：

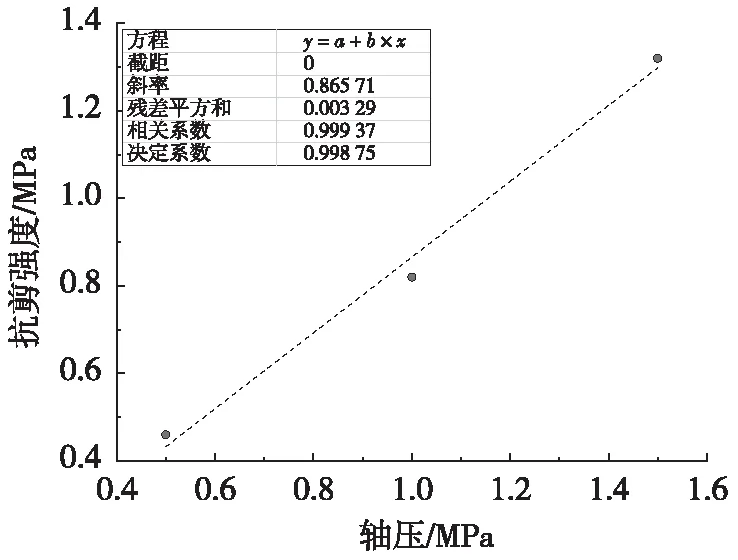
图5 忽略粘聚力作用抗剪强度分析

(3)

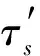
表2 2种回归分析条件得到的拟合参数

回归分析的原则是在设定条件下使得离散数据与拟合曲线间残差平方和最小，因此考虑粘聚力情况(仅设定拟合函数)下拟合得到的残差平方和要小于忽略粘聚力的情况(设定拟合函数和截距)下的，但是忽略粘聚力情况下的相关系数及决定系数较考虑粘聚力情况下的更接近于1，表明拟合曲线与离散数据间的相关程度更高，因此在忽略粘聚力条件下的拟合方程仍可对试验得到的峰值抗剪强度进行拟合，可对平直结构面抗剪强度进行较好的描述，因此无填充硬性平直结构面抗剪强度可以表示为：

(4)

3)JRC-JCS模型分析方法研究

根据Barton[12]提出的JRC-JCS模型对直剪试验结果再次进行回归分析，采用正交距离回归方法进行自定义函数拟合，结果如图6所示。

图6 JRC-JCS模型拟合结果

利用JRC-JCS模型可对该平直结构面等效基本摩擦角、结构面粗糙度系数进行估算。由图6所示拟合结果，结构面抗剪强度可用下式表达：

τJRS=σtan[39.8+0.145lg(2.35/σ)]

(5)

式中：τJRS为考虑结构面粗糙度系数的抗剪强度。利用式(5)对试验结果进行拟合，得到决定系数为0.997 95，较为接近于1，因此该抗剪强度表达式与直剪试验数据的相关程度较高，可用于描述平直结构面抗剪强度。从式(5)可看出，该平直结构面基本摩擦角为39.8°，结构面上下岩体粗糙度系数为0.145，粗糙程度较低。

2.2 齿状结构面剪切试验过程分析

针对齿状结构面起伏程度、轴压对抗剪强度的影响规律，分别选择结构面剪胀角为0°、15°、30°、45°齿状结构面开展直剪试验。试验剪切法向压力分别设置为0.125 MPa、0.25 MPa、0.375 MPa、0.5 MPa，试验同样采用应变控制式，设置剪切速率为5 mm/min。加载方式为分步加载，先施加法向力达到预定值保持不变，然后以一定速率施加切向力至预定剪切位移。试验设置剪切距离为30 mm，剪切试验过程中对切向应力、位移及法向应力、位移数据进行实时监测，数据采集频率为3.9 Hz。

2.2.1 剪应力-剪切位移关系分析

选择爬坡角为30°的齿状结构面试样进行轴压为0.125 MPa、0.25 MPa、0.375 MPa、0.5 MPa的直剪试验，结果如图7所示。

从图7可知，在0.125 MPa轴压条件下，剪切试验初始阶段剪应力增速缓慢，破坏过程具有一定的滑动破坏特征，强度峰值出现后随着剪切位移的持续增加，结构面的抗剪强度不断降低；在0.25 MPa轴压条件下，试样剪切初始阶段剪应力增速加快明显，剪切应力达到峰值后，结构面的抗剪强度快速降低，其破坏过程体现出明显的峰值剪断破坏；在0.375 MPa和0.5 MPa轴压条件下，剪切试验一开始，结构面咬合过程较短，随即发挥较大的抗剪强度，剪切应力达到峰值后结构面剪切应力急剧下降，表明试样已剪切破坏。

图7 30°爬坡角结构面剪应力与剪切位移关系曲线

2.2.2 剪胀特性分析

为分析齿状结构面的剪胀特性，选择30°爬坡角的结构面分别开展0.125 MPa、0.25 MPa、0.375 MPa和0.5 MPa四种不同轴压条件下的剪切试验，结果如图8所示。

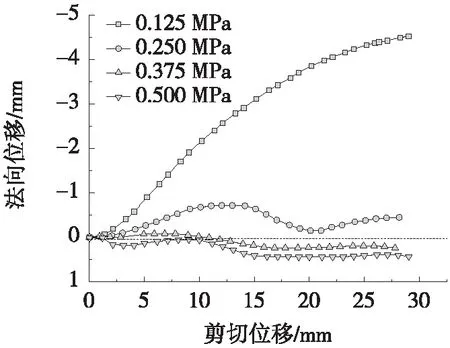
图8 30°爬坡角结构面剪胀特性分析

从图8可见，在0.125 MPa轴压条件下，剪切试验过程中爬坡效应明显；在0.25 MPa轴压条件下，剪切试验过程中同样出现爬坡效应，但剪胀效应相对减弱，法向位移明显小于0.125 MPa条件下，且未出现持续的剪胀；在0.375 MPa轴压条件下，剪胀效应进一步减弱，剪胀量峰值出现时间进一步缩短，由于轴压的增加，试样剪切过程中法向位移速率明显降低，剪胀量达到峰值后随着剪切位移的进一步发展，试验出现剪缩；在0.5 MPa轴压条件下，试样并未出现剪胀，随着剪切过程的不断发展，上下试样不断被压缩至结合紧密，期间由于齿状凸起的存在，法向位移随着剪切过程的发展存在一定的起伏。

2.2.3 爬坡角对结构面剪切过程的影响

选择0.5 MPa轴压条件，针对不同结构面预设爬坡角0°、15°、30°、45°开展直接剪切试验，可得到不同爬坡角条件下的齿状结构面剪切过程，结果如图9所示。

图9 结构面爬坡角对剪切过程的影响

由图9可见，随着结构面初始爬坡角的不断增加，结构面峰值抗剪强度不断增加，抗剪力峰值出现的时间也不断提前。不同爬坡角也反映了结构面粗糙程度，随着结构面粗糙程度的不断增加，结构面剪切刚度不断增大，剪切初期的抗剪强度增速逐渐加快，尽管结构面能够提供的最大抗剪强度不断增大，但特定单轴抗压强度下，结构面随着粗糙程度的不断增加，抗剪强度峰值出现时间越来越早，峰值后下降速度不断加快，即一定的单轴抗压条件下，粗糙程度增加后，材料剪切破坏体现出较为明显的脆性特征。

2.2.4 粗糙结构面抗剪强度分析

1)基于JRC-JCS模型的峰值抗剪强度分析

利用Barton[12]提出的JRC-JCS模型对齿状粗糙结构面的抗剪强度进行计算，结果如图10所示。

图10 JRC-JCS模型峰值抗剪强度分析

由图10可见，当结构面爬坡角为15°、45°时，试验得到的结果与计算结果较为接近，试验测得峰值抗剪强度略大于计算值，而当结构面粗糙度系数为0.15时，即平直结构面在0.5 MPa轴压条件下能够发挥的峰值抗剪强度略大于计算结果，而30°爬坡角的结构面实测峰值抗剪强度与计算结果差别较大，实测值小于计算值0.049 MPa。

2)弹性段剪切刚度分析

通过对粗糙结构面分别开展0°、15°、30°、45°爬坡角条件下的直剪试验，可获得齿状结构面弹性剪切变形阶段的剪切刚度，大致与结构面粗糙度系数成正相关线性关系，通过对其进行回归分析，获得结构面粗糙程度对剪切刚度的影响规律，如图11所示。

图11 结构面粗糙程度对剪切刚度的影响

由图11可得粗糙结构面剪切刚度与结构面粗糙度系数之间大致满足如下关系式：

k=0.013JRC+0.042 97

(6)

式中：k为结构面剪切刚度，MPa/mm。由图11可知，决定系数为0.95，残差平方和为0.001 35，较接近于0，可认为式(6)与试验结果相关程度较高，在一定程度上能反映结构面粗糙度系数与弹性段剪切刚度之间的关系。

3 结论

通过室内模型试验，对不同粗糙程度的花岗岩硬性结构面进行了抗剪强度分析，通过分析试验结果，得到如下结论：

1)岩体结构面抗剪力峰值随着法向压力的增加而增大，结构面剪切刚度随着法向压力的增加而增大。

2)岩体结构面剪切过程中存在抗剪力峰值，在低法向压力作用下，岩体结构面抗剪力达到峰值后，随着剪切位移的增加，结构面抗剪强度无明显回落；而在高法向压力作用下，岩体结构面抗剪力达到峰值后，随着剪切位移的增加，岩体结构面抗剪强度存在较为明显回落现象。

3)岩体结构面在剪切过程中，剪胀分量的发展情况与结构面一阶凸起的抗剪力息息相关，而摩擦分量则随着剪切位移的变化与花岗岩硬性结构面二阶凸起的抗剪力的发挥过程关系密切。