基于LFSTM 的数学课堂“凝聚”*
欧阳亮 胡典顺
(华中师范大学数学与统计学学院,湖北武汉 430079)
现阶段课程体系包含国家课程、地方课程和校本课程,地方课程和校本课程是对国家课程的补充和完善.虽然地方课程和校本课程在设置和选择上有较强的自主性,但教育教学活动依然是以学科知识、方法、技能为主,学科思维为辅.这种教育教学活动重在知识学习的系统性、完整性和严谨性,有助于学生系统地掌握知识,实现“双基”目标,虽然在教育中也渗透着对数学思维的培养,但关注程度依然不够.张景斌、王尚志[1]指出数学教育本质上是理性思维的教育.本文基于LFSTM 的数学课堂“凝聚”,除了关注学生“双基”“六能”的培养外,还注重学生数学思维的建构.
一、LFSTM的分析
(一)中学数学解题的LFSTM模式
把数学解题过程中,指引等价辅助题目链朝着元素化少、化熟和化同的方向进行变换的思维模式称作“少熟同思维模式”(Less-Familiar-Same Thinking Model),即LFSTM[2].LFSTM为中学数学解题等价辅助题目链的产生提供方向.
(二)LFSTM为课堂的转变带来契机
1.LFSTM 体现知识模块间思维习惯的异同,实现不同模块知识之间思维习惯的整合,达到“牵一发而动全身”的效果
传统的数学思想方法严谨而系统,但在问题解决的靶向上缺乏指导,从而导致很多学生在习得知识与技能后,不会应用于实践,不会灵活地分析和解决问题.这和传统教育教学活动主要是按知识、方法和技能开展的有关,这样的方式让学生往往缺少对各种知识、方法、技能之间联系的感知,造成整体思维的割裂.学习是存在迁移的,迁移产生一部分是由于思维能力的提高,而另一部分是由于各种知识、方法和技能之间存在思维的相似性,这种相似性的发现有利于学生对新知识、新方法和新技能的习得以及思维、知识体系网络化的形成.
2.LFSTM回答了数学问题解决活动中的“为什么”,实现对两个“为什么”的明确合理的阐述
现在绝大部分教师在教学中往往对“为什么”没有做出合理的解释,对学生数学元认知和批判性思维的培养有所欠缺,特别是在解决比较复杂的问题上.比如,该问题“为什么”要这样分析和处理?“为什么”要形成这样的思维习惯?“为什么”其他思维方式不合适?等等.这些“为什么”的合理解决恰恰是教师素养和素质的体现.
“为什么”问题要这么解决?“为什么”问题不这么解决就不可以?这两个“为什么”从元认知和批判性思维的角度给出,是数学思维培养的关键点.比如,“为什么”问题要这么解决,是因为前提、背景的原因,还是结论、目标的原因,还是具体思维习惯的原因,还是知识本身发展规律的原因等.这些原因的弄清是一个很有意思的过程,会给学生带来成就感,激发对数学学习的兴趣.
3.知识来源于生活,LFSTM是对生活的提炼、抽象和总结
教师的教育教学要融入生活的元素.这些元素不单单是生活的实例或以生活为背景,更重要的是生活与知识在思维习惯上的融合(比如,生活中我们如何思考解决一个棘手的问题?而在学科问题上是否也有相同的思维习惯?).但这恰恰就是现在教育教学中缺少的一个环节,因为这个环节的缺少导致很多学生觉得学习是枯燥的、无聊的.
数学源于生活,数学的思想方法也源于生活.生活中我们解决问题总是喜欢简洁简单的处理方式,喜欢应用自己熟悉的处理方法.数学的思维模式也是如此.对于高中学生来说什么是容易解决的数学问题?答案是一定的:未知数少、参变量少、次幂少、问题模型熟悉、问题模式相同等.简洁一点说就是要“少”“熟”“同”.所以解决实际生活问题和解决数学问题的思维模式是趋同的.
二、基于LFSTM的课堂实践
我们以高中数学函数值域的求解为例来进行展示、分析和说明.
(一)以“少”解题——案例1:函数值域求法一

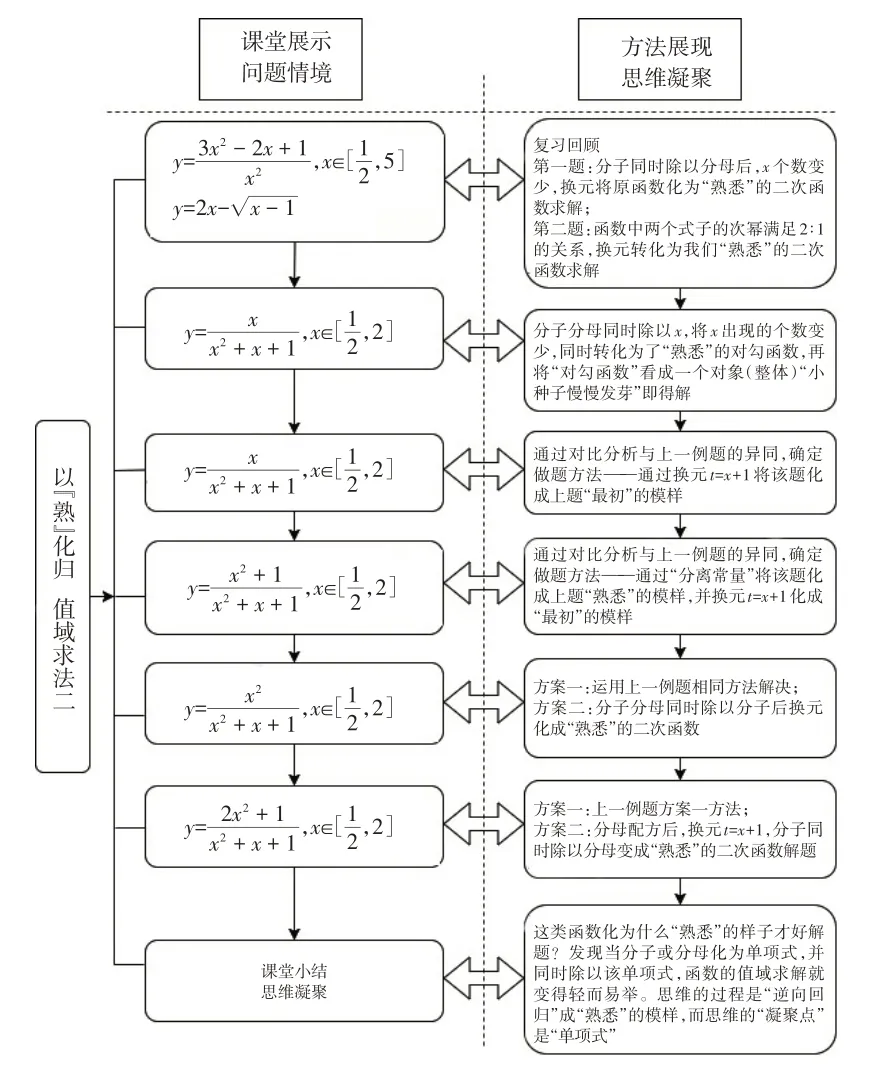
(二)以“熟”化归——案例2:函数值域求法二
三、基于LFSTM的数学课堂“凝聚”
(一)数学方法的“凝聚”
1.案例一课堂分析
在本节课中,教师尽量淡化数学的解题方法,将方法“凝聚”为“化少”,更多地强调数学解题等价辅助题目链的产生是朝着“化少”展开的.在“化少”的思维引导过程中,自然而然地把传统的思想方法渗透进来,达到“润物细无声”的效果.比如,在求值域的化少过程中,就悄无声息地融入“配方法和分离常量法”,避免了生搬硬套和学生在不理解的情况下死记硬背.
2.案例二课堂分析
在本节课中,教师采用变式教学,环环相扣,引人入胜.在变式的设计、利用变式开启学生的思维上,紧紧围绕“化熟”来展开.每一变式的思考方向都是指向前面“熟悉”的例题,将方法“凝聚”为“化熟”.而课堂最后的画龙点睛“在生活中,何尝不是如此.我们在处理新事物时,总是参照我们‘熟悉’的、‘类似’的事物入手,尽量用我们‘熟知’的方式方法来解决”更是将生活与数学相融.由此,让学生从生活中深刻领悟“化归”思想,以达到熟练应用的目的.
(二)数学思维的“凝聚”
1.以“少”为中心的“凝聚”
课堂上,在教师的启发、引导下,学生的学习激情被点燃,思维逐渐深入,拾级而上,最后对问题解决的“画龙点睛”让思维“返璞归真”.如案例1,问题设置x的个数逐渐增多,师生互动紧紧围绕如何将x的个数变“少”而展开,中心目的明确,但思维强度逐渐增加.围绕变“少”这个核心,让思维发散,但“散(sàn)而不散(sǎn)”,特别是“大家回想下我们生活中处理问题的时候,是不是也是寻找‘最简洁’的处理方式,而‘最简洁’何尝不是‘少’呢?”让生活和数学趋同,让数学问题解决的思维“返璞归真”.
2.以“熟”为中心的“凝聚”
课堂中教师提问能有效激发和维持学生的思维,并实现思维的“凝聚”.教师根据关键教学事件设计核心问题串来激发学生的思维[3],一系列提问的背后蕴藏着学生对问题的深入思考.课堂上师生之间是朋友,大家热烈地讨论,相互“质问”,思维在碰撞与交锋中升华.如案例2,问题串的设计将前一个问题作为后一个问题的“熟悉”的范例,让学生在问题解决的过程中体会如何将“陌生”问题转化为“熟悉”范例.而所产生的解题方法分歧与思维碰撞,让学生的思维得到升华.一句“大家可以发现分子和分母中,只要有一个化成单项式后,函数的值域就好求了!”点出问题串最“熟悉”的范例,展示问题串“万变不离其宗”的本质,让思维得到“凝聚”,这种“凝聚”实现思维从“过程”向“对象”的转化.郑毓信[4]指出数学的不少概念在最初是作为一个过程得到引进的,但最终却又转化成一个对象.案例中基于问题串的教学行为引导学生由解决问题的“过程”开始,经过问题变化,使得“过程”得到强化,最终形成学生个体心理图式中的“对象”.思维的“凝聚”过程,涉及学生个体的认知调节,包括计划、检查、监测、修改、评价等,让学生在此过程中体会到元认知策略性思考与调控的重要.
(三)课程内容的“凝聚”
课堂是基于LFSTM 设计的,所以课程内容在落实课程标准的同时对课程内容进行了重新调整.这种调整包括课程内容顺序上的调整和分类的调整.比如在函数值域教学内容的安排上,是以LFSTM 为顺序对内容进行编排的,依次讲解化“少”和化“熟”,这与以往的以问题解决方法为顺序编排的教学内容不相同.以问题解决方法为顺序编排的教学内容没有体现方法之间的联系,没有揭示思维的本质.比如求值域的配方法、分离常量法、辅助角公式、换元法等在以往的课程安排中都是独立的,问题解决方法之间没有联系,但是在LFSTM 下,这些方法都可以划归到化“少”的范畴.由于在LFSTM 基础上设计的课程不再完全按照问题解决的方法来对内容进行划分,所以内容的分类也进行了相应的调整.这种调整就是由以方法为依据进行的课程内容分类变为了以LFSTM为依据的分类.以LFSTM为依据的分类在体现原有问题解决方法的同时,重点强调方法的异同和联系,并从思维模式上对这些方法进行原理分析,从思维上对课程内容进行重新“凝聚”.
通过案例的展示和分析,我们发现LFSTM 体现中学数学问题解决技能、方法之间的联系,有利于学生对数学的整体理解和掌握,有利于思维的“凝聚”,有利于建构学生个体的数学心理图式,也有利于在问题解决过程中对个体心理图式中概念、知识和方法的提取.LFSTM 为中学数学解题等价辅助链的产生提供了方向,同时也为数学方法、数学思维和数学课程的“凝聚”带来契机.当然,这些“凝聚”是以思维的“凝聚”为中心,方法和课程的“凝聚”是为了更好地落实思维的“凝聚”.

