旋转位似“似”成双 定点定形“轨”一致
郭源源
(南京市金陵中学西善分校,江苏南京 210041)
初中几何中,由图形运动而产生的最值问题历来是学生解题的难点,究其原因是图形一直在变化,学生无法捕捉到运动变化背后“不变”的元素,难以分析出最值时的位置,也就无法从具体图形上分析求解.动态问题解题的关键在于动中寻找定的量,再由这些定量探寻出动点形成的轨迹,从而根据轨迹分析出最值位置,即“由动寻定,由定定轨,由轨求最”[1].因初中知识的局限性,初中的动点轨迹以圆和直线轨迹为主,而确定轨迹的方法通常有两种:其一,由“定点对定长”,依据圆定义确定轨迹,或者由“定弦对定角”依据圆周角定理确定圆轨迹;其二,旋转位似变换,因绕定点变换过程中,图形形状始终不变,故可由一个动点的轨迹,确定其他动点的轨迹,即“定点定形轨一致”.相比之下,后者的原理更加隐蔽灵活.本文就以旋转位似变换为例,介绍这类变换所蕴含的性质及在解题中的运用,与大家交流分享.
一、旋转位似变换介绍
旋转位似变换是指一个图形绕一定点作旋转变换的同时,也作位似变换;它是旋转变换和位似变换的复合变换,此时的旋转中心和位似中心相重合.
【结论】若一个图形绕一个定点作旋转位似变换,则图形上所有点的运动轨迹呈现形状一致性,且任意两点运动的路径长之比等于它们到旋转位似中心的距离之比.其中:
(1)若一个点的轨迹是直线,则另一点轨迹也一定是直线,且两直线夹角与这两点和旋转位似中心组成的夹角相等或互补,即如图1,点B的轨迹l和点C的轨迹l′的夹角与∠BAC相等或互补;
(2)若一个点的轨迹是圆,则另一点轨迹也一定是圆,且两圆心和旋转位似中心组成的夹角与这两点和旋转位似中心组成的夹角相等,两圆心到旋转位似中心的距离之比等于这两点到旋转位似中心的距离之比,即如图2,
【证明】
(1)如图1,当点B在直线l上运动,由旋转和位似的性质可得:进一步可证△BAB′CAC′,得和∠ACC′=∠ABB′,再由四边形内角和和邻补角易证∠α=∠BAC为一定值,故C点在与∠α=∠BAC的直线l′上运动.
(2)如图2,当点B在⊙O上运动时,作点O′使进一步可证△ACO′,得由k和OB为定值,可推出O′C始终也为定值,故点C在以O′为圆心的圆上运动,且⊙O和⊙O′的半径之比等于k.
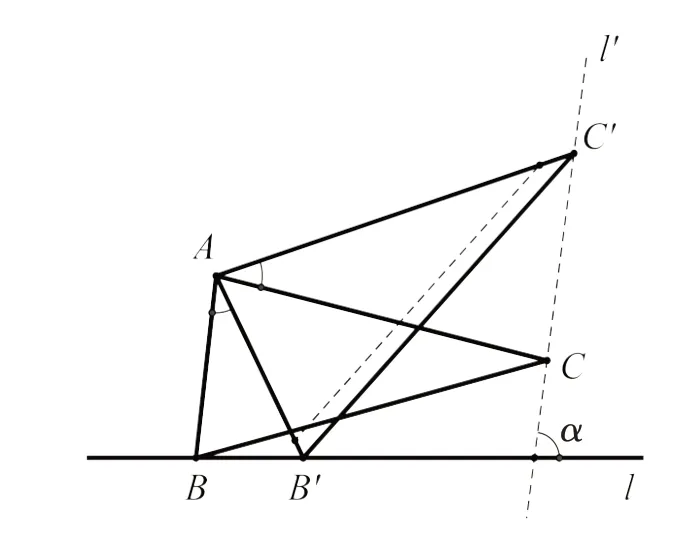
图1

图2
【评注】这种图形运动的实质是旋转和位似,因为旋转中心和位似中心重合,过程中具备“定点加定形”,所以始终存在两对相似三角形,即“双相似”.由双相似致使角的等量关系和边的比例关系一直存在,所以AB以一种关系在变化,AC就以同样的关系在变化,即轨迹形状呈现一致性.所有轨迹中,直线和圆的轨迹最为常见,其他轨迹证法亦是同理.
二、旋转位似变换应用
(一)保“形”不变,调整图形位置
例1如图3,平面上有任意三条不等距的平行线,使用尺规做出一个等边三角形,要求三角形的三个顶点分别在这三条平行线上.
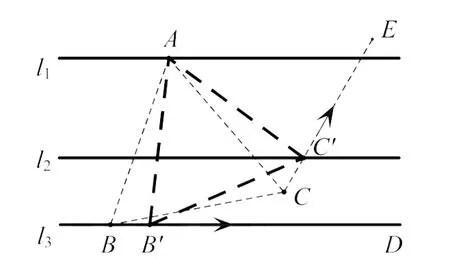
图3
【分析】借助特殊到一般的思想,等边三角形三个顶点都位于三条平行线上若作不出,那思考两个顶点呢?两个顶点位于两条平行线上的等边三角形很容易做出且有无数种,如△ABC.接下来就是在保证等边的前提下转移图形位置,利用旋转位似变换由点B在直线l3上的运动,可确定点C的直线轨迹,当点C运动到l2上时就是等边三角形的目标位置.
【作法】限于篇幅,只写作法思路,如图3.
1.在l1和l2上任取两点A和B,作等边三角形ABC.
2.作射线CE,使得∠ACE=∠ABD,交l2于点C′.
3.连接AC′,以AC′为边作等边三角形AB′C′.
△AB′C′即为所求.
【评注】因等边三角形的旋转位似,所以有△ABB′△ACC′,故第3 步确定点B′的做法还可以是在l3截取BB′=CC′或者是作射线AB′,使得∠C′AB′=∠CAB,交l3于点B′.此题的等边三角形还可以变式为等腰直角三角形或其他特殊三角形,作法思路都是先构造再调整,即借助旋转位似变换,在保证形状不变的前提下,调整图形位置.
变式1如图4,∠AOB的内部有一点P,使用尺规作等腰直角三角形PCD,要求点C、D分别在射线OB、OA上,∠PCD=90°.
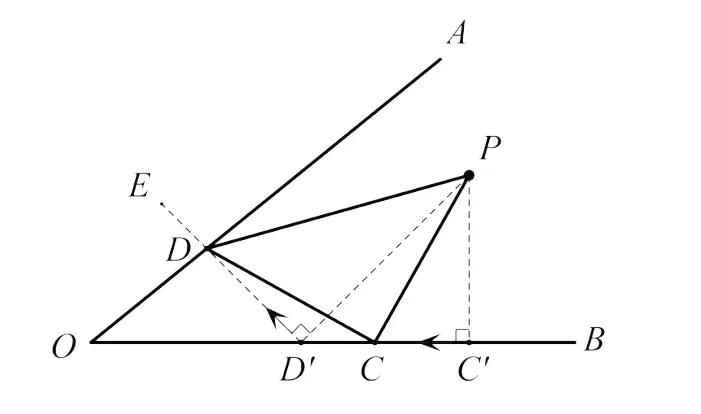
图4
【分析】易构造出等腰直角三角形PC′D′,借助旋转位似变换,当点C′在射线C′O上运动时,点D′也一定在射线D′E上运动,且∠PD′E=∠PC′O=90°.这样D′E与OA的交点即为点D的位置,点D确定则点C随之确定.
【作法】
1.作等腰直角三角形PC′D′,如图4.
2.作射线D′E,使得∠PD′E=∠PC′O,交OA于点D.
3.连接PD,作射线PC,使得∠DPC=∠D′PC′,交OB于点C.
4.连接CD,△PCD即为所求.
变式2 如图5,⊙O外有一点P,使用尺规作等边三角形PAB,要求点A、B分别在⊙O、曲线l上.
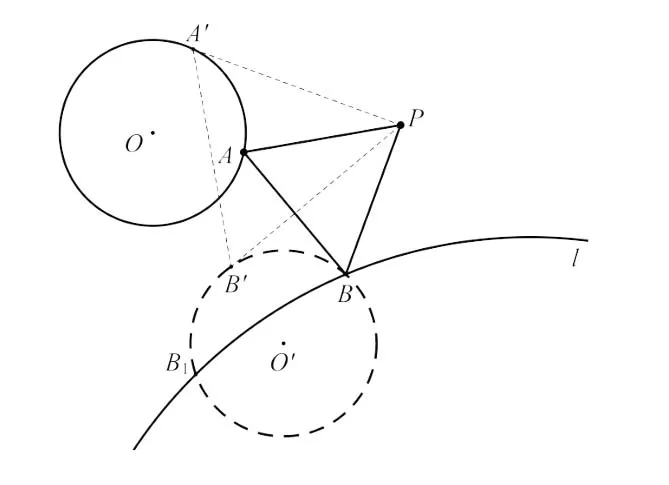
图5
【分析】⊙O上任取一点A′,易构造出等边三角形PA′B′,借助旋转位似变换的结论,当点A′在⊙O上运动时,点B′也一定在⊙O′上运动,且圆心O′的位置满足△POO′为等边三角形.这样⊙O′与曲线l的交点即为点B的位置,点B确定则点A随之确定.
【作法】
1.⊙O上任取一点A′,作等边三角形PA′B′,如图5.
2.作等边三角形POO′.
3.以O′为圆心O′B′为半径作⊙O′,⊙O′交曲线l于点B、B1.
4.连接PB,作射线PA,使得∠BPA=∠B′PA′,交⊙O于点A.
5.连接AB,△PAB即为所求(△PA1B1作法亦是同理).
【总结】三角形多个顶点位于特殊位置的作图,直接瞄准最终位置难度太大,可先着眼于部分顶点,再借助旋转位似变换,确定运动轨迹后调整图形到目标位置.这种从“轨迹”上研究问题的视角,不仅可以解决一类作图问题,还可以进一步培养学生动态分析图形的数学眼光.
(二)定“形”视角,研究内嵌面积
例2如图6,有一张边长为4cm的正方形铁片,现从中剪一个两直角边比为4∶1的直角三角形铁片,则这样的直角三角形最大面积为________cm2.
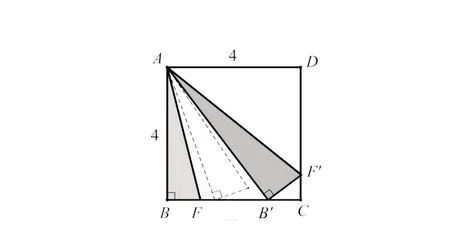
图6
【析解】学生最易想到的剪法是沿着正方形的一边和直角剪,即△ABF,可这是最大的4∶1 直角三角形吗?借助旋转位似变换,4∶1直角三角形的直角顶点在由B向C上移动的过程中,形状不变,面积越来越大.不难发现当F运动到CD上时,此时直角三角形面积最大,即求△AB′F′的面积.
由一线三直角得△ABB′△B′CF′,易求出B′C=1,BB′=3;在Rt△ABB′中,由勾股求得AB′=5,所以
变式3(2017年中考南京卷)用一张正方形铁片剪一个直角边长分别为4cm 和1cm 的直角三角形铁片,所需正方形铁片的边长的最小值为________cm.
【析解】正方形固定,求内部最大内嵌的特定形状三角形;三角形固定,求外部最小覆盖的正方形.这两个问题本质是相通的,所以本题可以转化成例2的问题,当直角边长分别为4cm 和1cm 的直角三角形为△AB′F′时,正方形ABCD就是它的最小覆盖正方形.根据例2相似的方法,易求得
变式4有一张腰长为4cm的等腰直角三角形铁片,现从中剪一个两直角边比为4∶1的直角三角形铁片,求直角三角形的最大面积,并画出示意图.
若“等腰直角三角形”变为“等边三角形”,最大面积又该如何画?

图7
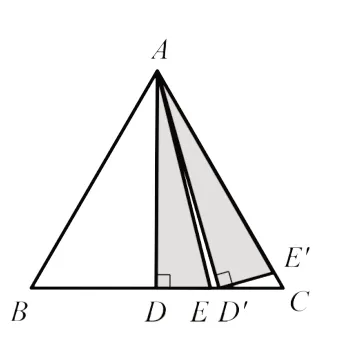
图8
【析解】如图7,首先最易想到的剪法是沿着等腰直角三角形的一边和直角剪,即△ABD;再借助旋转位似变换,当△ABD运动到△A′BD′时,面积最大.△A′BD′面积求法仍然沿用一线三直角构造相似易求得进一步可求出
若变为等边三角形,如图8,首先易想到△ADE,再借助旋转位似变换,当△ADE运动到△AD′E′时,面积最大,求法同上.
【总结】求几何图形面积的最值通常有两种方法.一是解析法,设x建立函数关系式求解;二是构图法,用运动眼光看问题,找到最值位置求解.后者对图形思维要求更高,而旋转位似,这种定“形”变换的动态视角,恰恰是巧妙解决这类问题的方法之一.
(三)由“形”定轨,确定最值线段
例3(2020年中考泰安卷)如图9,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为________.
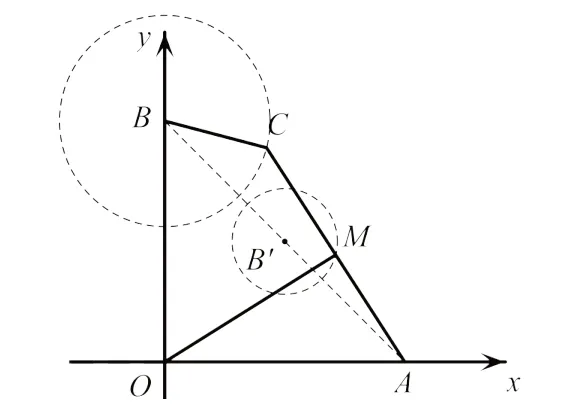
图9
【析解】如图9,由BC=1 易知点C在半径为1的⊙B上运动.因为A为定点,M始终是AC中点,可理解为运动过程中形状不变,借助旋转位似变换可知点M的运动轨迹也一定是圆.由中位线进一步可确定点M在以AB中点为圆心的⊙B′上运动.
由A、B坐标求得B′坐标为(1,1),⊙B′的半径所以OM的最大值为OB′+r
变式5如图10,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,△MAC为等腰直角三角形,∠CMA=90°,连接OM,则OM的最大值为________.
【析解】如图10,点A的位置和△MAC的形状始终不变,即具备定点和定形,所以由旋转位似变换可知当点C在⊙B上运动时,点M也一定在⊙B′上运动,且圆心B′的位置满足△ABB′△ACM,这样点M的轨迹即可确定.

图10
求得B′坐标为(2,2),由旋转位似中存在的双相似易知△AMB′△ACB,所以得故OM的最大值为
变式6如图11,点A,N的坐标分别为A(2,0),N(1,0),点C的坐标为C(a,2),△MAC为等腰直角三角形,∠CMA=90°,连接NM,则NM的最小值为________.
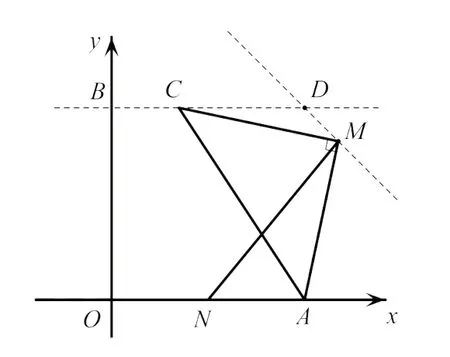
图11
【析解】如图11,点C在纵坐标为2的直线上运动,△MAC同样具备定点A和定形.由旋转位似变换的结论可知当点C在直线BC上运动时,点M也一定在直线DM上运动,且两直线的夹角等于∠CAM为45°,这样点M的轨迹即可确定当点C运动到y轴上时,点M到达点D处,可求得点D坐标为(2,2).由夹角45°可求出直线DM与x轴的交点坐标为(4,0).所以易求出点N到直线DM的距离即为NM的最小值.
三、旋转位似变换感悟
特殊轨迹的形成,究其原因是在运动的过程中存在着一些不变的定量关系,这些定量约束着动点的变化,从而形成特定的轨迹,如本文中的旋转位似变换,过程中始终存在着“双相似”,相似确定则数量关系和位置关系确定,即轨迹确定.这种旋转位似确定轨迹的方法,也仅是轨迹法中的一种,通过原理介绍、题目变式、方法提炼,使学生在解决这类问题中能够化繁为简、化动为定、化隐为显,生成“定点定形轨一致”的感悟.
荷兰著名学者弗赖登塔尔认为数学教学方法的核心是学生的“再创造”,也就是学习过程应注重知识方法的自我发现,并善于总结经验实现再次迁移运用.题目只是知识方法的一个素材,通过解题的过程,让学生理解知识的原理,提炼方法的本质,注重解法的策略,总结问题的归类,从而达到利用有限的题目实现无限的再创造.由解一道题变成会解一类题,乃至通解一种体系的题,这也是解题教学的方向[2].


