不同虚拟横梁对箱形梁桥自振频率的影响探究

张长亮，晋民杰，冯保杰

(太原科技大学 交通与物流学院，太原 030024)

桥梁做为实现交通的基本条件，它的安全与否，对居民安全出行有着重要的作用。为了满足日益增长的交通需求，我国的道路设计越来越宽，桥梁跨度和宽度增大很快。桥梁自振频率，是桥梁结构最重要的基本动力特性之一，也是桥梁安全与否的主要因素之一[1-2]。因此，自振频率的准确获取，在实际工程中显得至关重要。目前，较为常用的方法是脉动试验法与跳车实验法[3]。对桥梁的动力特性研究可以追溯到20世纪中叶，以Willis[4]对Britannia桥进行的动力特性试验。谭国金教授建立了多个车辆作用下桥梁的固有频率频率计算方法[5]。本文在前人研究的基础上，模拟不同虚拟横梁的截面形式，分析桥梁的自振频率，并与实桥测试频率进行对比分析，其研究成果可为该类桥梁的频率计算提供参考。

1 梁格法基本原理

梁格法采用等效梁格代替实际结构，将等效梁格的刚度代替邻近实际结构的刚度，如截面的抗扭刚度和弯曲刚度等，当两者在相同荷载下，其挠曲线相同，因两者结构特性上的差异，等效梁格的内力只能近似等效实际结构的内力[6-8]。

1.1 梁格法基本假定

(1)各纵梁横截面尺寸与桥梁纵向长度比值较小(一般L/B>3即可)，实际结构简化为集中在沿梁纵向轴心的弹性杆件。

(2)在钢筋混凝土和预应力混凝土桥梁结构中，截面受到翘曲正应力和剪应力与结构所受弯矩和扭矩的应力值相比很小，采用纯扭转理论分析。

(3)刚性截面假定，梁体受力后截面不发生形变。

(4)平截面假定，梁体受力形变后截面仍然保持在同一平面(即不发生翘曲)。

1.2 梁格划分应考虑的因素

(2)横向联系一般采用间隔1 m的虚拟横梁进行横向连接，并应增加支点、1/8跨、3/8跨、1/4跨、3/4跨和跨中处的横向联系，以保证横向传力。

(3)由于梁格划分后边纵梁几何形状的非对称性，这显然与实际受力情况不符，在计算结果的分析中应消除平面外弯矩产生的效应。

1.3 慧加梁格法

慧加梁格法，即在已有的梁格法理论基础上，无需要求各纵梁形心位置均和原截面保持一致，即分割截面后各纵梁的形心位置不变，采用横向梁格将各纵向梁格联系在一起，形成一个单层的折面格构式模型，实现截面任意位置和个数的划分，梁格刚度修正方便，缩短建模时间[9]。

在进行桥梁建模时，为了缩短工作时间、提高工作效率，采用简便快捷的建模方法显得至关重要，因此采用慧加梁格法对桥梁模型进行建立。

2 建立仿真模型

2.1 工程概况

本文以某匝道18 m+20 m+18 m连续单箱双室宽翼缘板箱梁桥为例，采用通用有限元分析软件Midas civil，基于慧加梁格法的基本理论，建立仿真模型，其支点，跨中截面如图1所示。

图1 依托工程截面尺寸示意图Fig.1 The schematic diagram of project section size

2.2 梁格划分

因为梁格体系与实际工程结构存在一定偏差，因此在运用梁格体系对结构进行模拟时不可能达到理想效果。在运用慧加梁格法对桥梁上部结构进行划分时由于截面划分方法的不同，各纵梁横向连接形式的不同，模拟出来的结果也不尽相同。为建立各纵梁的横向联系加强整体性，还应设置虚拟横梁[10]。

2.2.1 截面划分

本文基于慧加梁格的基本理论，采用Midas civil建立有限元模型，其仿真如图2所示，其中单元数为380，节点数为171.横截面梁格划分参照慧加梁格理论进行划分，其划分形式如图3所示。

图2 仿真示意图Fig.2 Simulation diagram

图3 截面梁格划分示意图Fig.3 Schematic diagram of section girder division

2.2.2 虚拟横梁选取

黑洞——一种密度大到连光都无法逃逸的天体——是爱因斯坦广义相对论的一个惊人产物。广义相对论认为，我们称之为“引力”的这种现象，实际上是时空几何的一种扭曲。根据这个理论，当某个地方集中了太多物质或能量后，时空就会产生变化：时间会变慢，物质会收缩并且消失在那些宇宙天坑（也就是黑洞）里。

利用慧加梁格法对箱梁进行划分，并设置横向连接虚梁来进行各纵梁之间横向力的传递。但由于虚拟横梁的选取方法较多，不同的截面形式，对应的结果也不尽相同，本文基于工程的相关经验，采用三种不同的虚拟横向的截面形式，分别为矩形截面、I字形截面、工字形截面三种横向连接截面形式，具体截面形式如图4所示，各截面特性如表1所示。

图4 三种截面形式Fig.4 Three cross-sectional forms

表1 截面特征对比表Tab.1 Comparison table of cross-section feature

注：Asz——单元局部坐标系y轴方向的有效抗剪面积；Asy——单元局部坐标系z轴方向的有效抗剪面积；Ixx——单元局部坐标系x轴的扭转惯性矩；Izz——单元局部坐标系z轴的扭转惯性矩；Iyy——单元局部坐标系y轴的扭转惯性矩；Qyb——单元局部坐标系y轴方向的剪切系数；Qzb——单元局部坐标系z轴方向的剪切系数。

2.3 Midas civil建模分析

2.3.1 建立仿真模型

本文采用慧加梁格方进行建模仿真，根据不同的虚拟横梁，建立三种有限元模型，具体如图5所示。

图5 不同横梁截面模型示意图Fig.5 Schematic diagram of models of different beam sections

2.3.2 不同虚梁连接形式

理论计算根据有限元理论采用Midas civil计算程序进行仿真模拟计算，在Midas civil中通过改变不同虚梁的截面形式，分别提取不同虚拟横向的自振频率，具体如图6所示。

图6 不同横梁截面自振频率图Fig.6 Frequency diagram of natural vibration of cross section of different beams

将三种桥梁的自振频率整理，具体见表2.

表2 不同虚拟横向截面下结构频率一览表Tab.2 List of structure frequencies under different virtual cross sections

3 动力特性测试方案

3.1 动力性能测试

目前，公路桥梁荷载试验方法主要包括静载试验法和动载试验法，为了有效的测取结构的动力性能，采用TMR-211动态数据采集仪采集动态数据[11]。依据桥梁振型图确定，在测试桥跨中截面附近桥面上安装传感器作为动载测点。为测得此桥的自振频率，试验过程见图7.

图7 动载试验图Fig.7 Dynamic load test drawing

3.2 结构频率测试分析

采用脉动试验得到的自振信号的各阶频率，时域曲线见图8.

图8 脉动时域曲线图Fig.8 Fluctuating time-domain curves

3.3 实验结果对比分析

提取桥梁结构的前两阶竖向频率，并与模型计算出来的理论值进行对比，结果如表3-4所示。

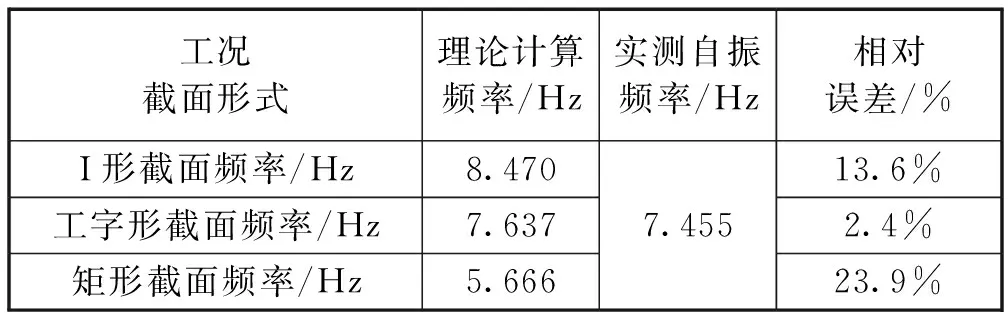
表3 结构一阶自振竖向频率实测值和计算值对比表Tab.3 Comparison table of measured and calculated natural frequencies of the first-order structure

从表3、表4可知，无论是梁的一阶自振竖向频率还是二阶竖向自振频率，虚拟横梁为工字形截面的自振频率理论值与实测桥梁自振频率最为接近，因此，本文建议采用工字形截面进行模拟，能够更真实的反映桥梁实际自振状态。

表4 结构二阶自振竖向频率实测值和计算值对比表Tab.4 Comparison table of measured and calculated natural frequency of second-order structure

4 结语

本文以某三跨箱梁桥为依托工程，基于慧加梁格法进行梁格划分，采用Midas civil进行建模仿真，模拟不同横向连接方式下，结构的自振频率值，并与桥梁的实际频率进行对比分析，得出虚拟横梁为工字型截面时，计算结果与实际频率更为接近，相对误差在5%以内，研究结果可为该类桥梁的仿真建模分析提供参考。