“判别式法”在追及、相遇问题中的巧妙运用
毛广文
“判别式法”是数学中常用的一个解题方法,若将此方法引入到物理的学习中,则可以使得物理问题的解答更加严谨和灵活。比如,在处理追及、相遇问题时,根据两物体的位移关系列出关于时间t 的一元二次方程,得出相遇时间t 的表达式,就可以通过对时间t的解来讨论相遇的可能性及相遇的次数,即通过对关于时间t 的一元二次方程的判别式“Δ=b2-4ac”的讨论来确定物体是否能够相遇,以及相遇的次数。下面举例说明。
例1 甲、乙两物体相距s,同时同向沿同一直线运动,物体甲在前面做初速度为零、加速度为a1的匀加速直线运动,物体乙在后面做初速度为v0、加速度为a2的匀加速直线运动,则( )。
A.若a1=a2,则两物体只能相遇一次
B.若a1>a2,则两物体可能相遇两次
C.若a1<a2,则两物体可能相遇两次
D.若a1>a2,则两物体可能相遇一次或不相遇
讨论:
(1)当a1<a2时,判别式“Δ”一定大于零,且 Δ >v0,时间t 有两解,但因时间t 不能为负值,故只有一解有物理意义,即两物体只能相遇一次,选项C错误。
(3)当a1>a2时,判别式“Δ”的值由v0、a1、a2、s共同决定,可能小于零、等于零或大于零,且 Δ <v0。若v20<2(a1-a2)s,即判别式“Δ”的值小于零,则关于时间t的方程无解,故两物体不相遇;若v20=2(a1-a2)s,即判别式“Δ”的值等于零,则关于时间t的方程只有一个解,故两物体相遇一次;若v20>2(a1-a2)s,即判别式“Δ”的值大于零,则关于时间t的方程有两个正解,故两物体相遇两次。因此当a1>a2时,两物体可能不相遇、相遇一次或相遇两次,选项B、D 正确。
答案:ABD
本题采用一元二次方程的判别式进行分析、解答,显得简洁、明快。为同学们进行抽象思维和逻辑推理训练提供了有效方法。
例2 甲、乙两质点相距s,质点乙在前,质点甲在后,沿着同一条直线,向同一方向同时开始运动。质点甲以速度v 做匀速运动,质点乙由静止开始以加速度a 做匀加速运动,在什么情况下质点甲才能追上乙? 在什么情况下质点甲追不上乙?
设两质点运动的时间为t,则甲、乙两质点的位移分别为
讨论:
(1)当Δ=v2-2as<0,即v< 2as时,方程无解,表明当质点甲做匀速运动的速度小于 2as时,质点甲不可能追上乙。
(2)当Δ=v2-2as=0,即v= 2as时,方程有唯一解,表明当质点甲做匀速运动的速度等于 2as时,质点甲可以追上乙,且两质点只相遇一次。
(3)当Δ=v2-2as>0,即v> 2as时,方程有两解,表明当质点甲做匀速运动的速度大于 2as时,质点甲可以追上乙,且第一次追上质点乙时的速度大于乙,之后将超过乙,随着质点乙速度的增大,质点乙将追上甲并超过甲,故两质点相遇两次,相遇的时间分别为方程的两个解。
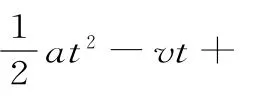
火车甲正以速度v1匀速行驶,司机突然发现前方距自己d 处有火车乙正以较小速度v2同向匀速行驶,于是他立即刹车,使火车甲做匀减速运动而停下。为了使两列火车不相撞,加速度a 应满足什么条件?

