结合虚拟迭代技术的整车级道路模拟试验方法

刘瑜瑾，王毅，段凯欣，张凯，胡玉倩

（北京福田戴姆勒汽车有限公司，北京 101400）

据统计数据表明，在现代工业领域中，约80%以上的机械零件破坏为疲劳破坏[1]。因此耐久性试验成为研发流程中揭示产品问题，同时提升产品质量的重要一环。相对于整车道路试验与CAE仿真试验，道路模拟试验具有不受天气条件制约、试验周期短、试验结果精度高、可重复性和可控性好等优点，有利于提高产品研发质量和效率[2]。与此同时，如何进一步结合计算机仿真提高试验精度，解决多系统同时验证时的迭代不收敛问题是本文关注的重点。

1 道路载荷谱采集

采集方案的制定需秉承着整车、台架、仿真联合验证的思路进行制定：根据待测系统特性、布置形式等判定台架试验形式，计算机分析需基于模态与疲劳分析提出意见，最后实地采集时还需要根据实际布点环境评估得到最终布点策略。

1.1 模态分析

试验模型由车架与各悬挂系统组成：油箱、电瓶箱、尿素罐等。它们的模态分析对布点策略及台架试验有重要的指导意义：1）在采集过程中关注其模态节点与波峰波谷点，以在台架试验过程中复现其振型；2）可在台架试验过程中规避迭代不收敛问题；3）通过频响计算可分析试验过程中失效问题。台架试验模型的前两阶模态振型如图1所示。在进行包含8 Hz与16 Hz的路段进行迭代时，由于振型被激发，可能会出现不收敛情况。因此若该两阶次振型与实车不一致，则需要进行试验模型修正，或避开振型的波峰波谷位置。

1.2 采集策略

道路载荷谱采集方案的确认是综合的，既要考虑试验关心，设计改进部位，又要兼顾实际操作的可行性，并尽可能反应车架及油箱运动姿态与应力分布特征。

1）模态节点与波峰、波谷点。为了进行道路激励再现，复现待测系统在整车行驶过程中的模态振型，模态节点与模态振型峰值点的选取可有效表征整个待测系统的模态振型。

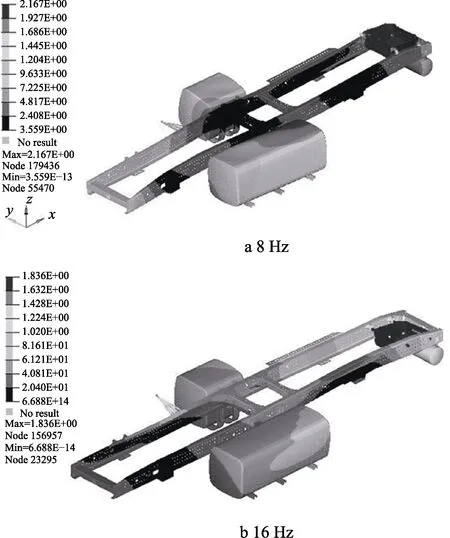
图1 试验系统模态分析结果Fig.1 Modal analysis result of system under test

2）台架试验关注点。即满足台架试验要求，使迭代收敛程度较高的点位。

3）布置便捷性。车架上搭载总成系统较多，且线束布置复杂，这会影响到应变片桥路策略选择和传感器、应变片粘贴[3]。

4）疲劳热点。即参考仿真疲劳分析，损伤较大寿命较短的位置，方便后期进行寿命对比。

2 疲劳损伤理论

2.1 线性损伤模型

线性损伤模型一般指的是Miner Rule。在本项目里，数据处理和损伤计算均采用LMS系列软件，所用的模型是Miner Rule。使用数学方法表示[5]：

2.2 循环计数法

循环计数法是将复杂的变幅加载历程简化为离散的简单横幅加载过程的有效手段。循环计数法包括单参数循环计数法（幅度穿越，波峰-波谷，区间计数）和双参数循环计数法（三点雨流计数法，四点雨流计数法）[4]。雨流计数法最早是由 Matsuishi and Endo在1968年提出的[6]。在LMS与Ncode软件中均运用四点雨流法，因为其对时域信号信息的保留更为完整。通过前期收集的道路载荷谱信号划分为Bin，产生新的采样点序列，使该序列仅包含波峰波谷（图2）。

图2 载荷谱简化Fig.2 Load Spectrum Simplification

四点雨流计数的原理为：对连续四个点进行计数，若内应力区间小于等于外应力区间，提取一个循环，并将中间两点丢弃，连接首位继续进行计数。无法计数的计为剩余点（Residue），跳过继续按上述规则计数。计数完毕后，所有剩余点拼接进行计数，最终剩余点无法计数的将载荷里程重组进行计数，直到所有点计数完毕。将所有循环信息统计至雨流矩阵中。该统计数据便是计算累积损伤的参数之一。试验过程中，将采集到的路谱按照该方法，每一段都进行预雨流计数，得到如图3所示的雨流矩阵。该矩阵给出了各应力水平下的循环次数，同时通过S-N曲线可知道各循环应力下的疲劳寿命，带入到公式（1）中便可以计算出损伤值了。

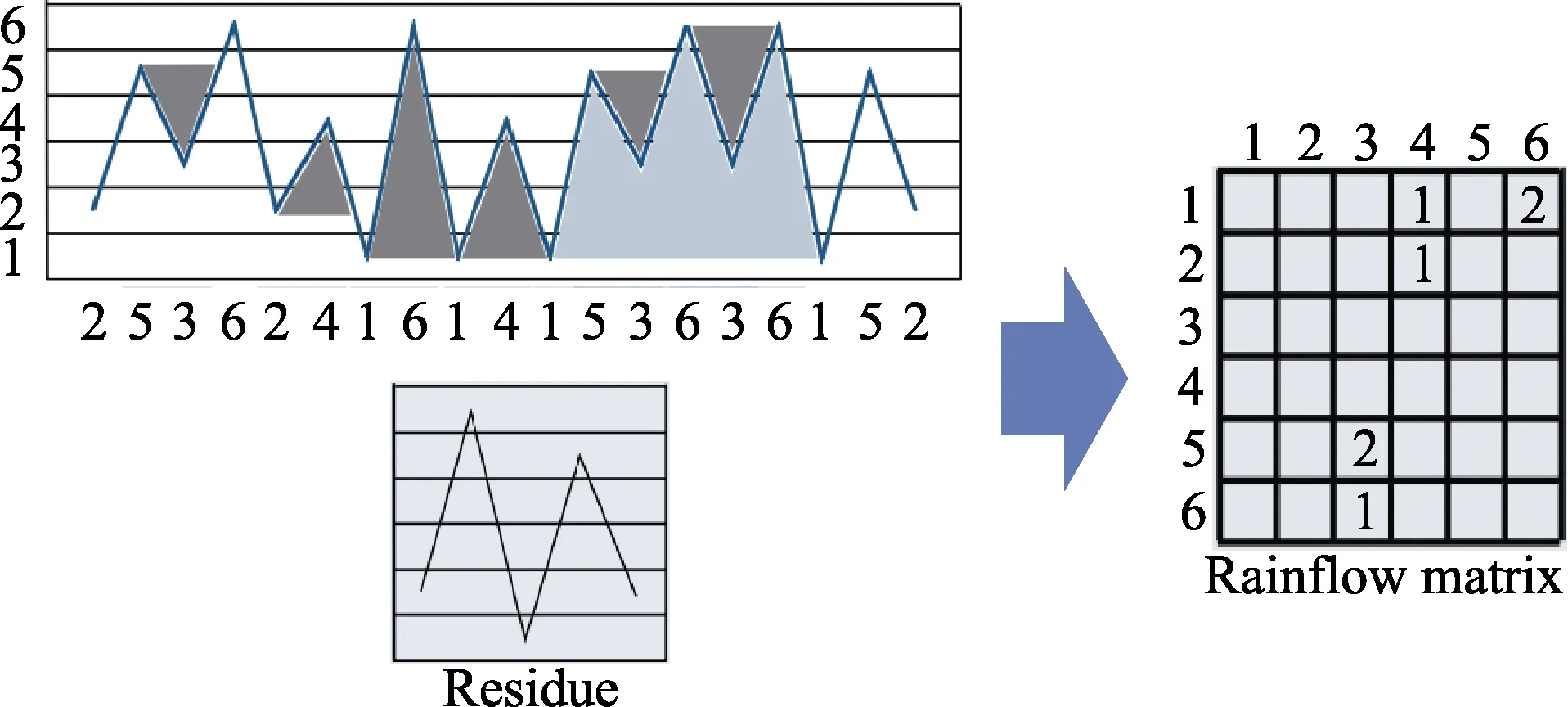
图3 雨流矩阵Fig.3 Rain-flow matrix

2.3 平均应力修正

影响疲劳寿命有两大关键因素：外加应力范围与平均应力。为补充平均应力在高周疲劳的影响，使用古德曼模型进行平均应力修正。如式（2）—（5）所示。

式中：Sr为应力范围；Sa为应力幅值；Sm为平均应力；R为应力比。同种材料，每个R值对应 1条S-N曲线，R对应的应力均值和疲劳极限点对应的应力幅值作为等寿命曲线的横、纵坐标，绘制成如图4所示的Goodman修正模型。对应力幅为Sa、平均应力为Sm的非对称循环Goodman修正模型等效为平均应力为0的对称循环，从而修正S-N曲线以关联损伤及平均应力。在试验中通过S-N曲线获取疲劳寿命计算损伤时，便需要按照上述过程进行S-N曲线的修正，随后再计算损伤。

图4 Goodman修正模型Fig.4 Goodman correction module

3 道路载荷谱编辑技术

在试验场采集到的道路载荷谱，由于采集信号链噪声、机械冲击及物理环境等因素会造成采集到的时域信号出现非正常表征：奇异点与趋势项。这些异常问题，需要在路谱正式编辑之前进行预处理。预处理完成后，进行路谱的正式编辑，使其满足台架试验需求。

3.1 道路载荷谱采集

通过长周期在全国范围内跟踪用户进行载荷谱采集，基于大数据关联的方法制定出试验场采集规范。采集序列包括：卵石路、坑洼路、直搓板、带角度搓板、甲种水泥路、乙种水泥路、长波路、短波路、小扭曲路、中扭曲路、比利时路等11种特殊路面。各路面以特定车速和次序进行采集。

3.2 幅值域筛选

需要对同一循环进行多次采集，选取统计学一致性较好的路谱，避免信号的偶然性干扰。如图5所示，同一循环采集了7次。其中Full-1-1最小值相对其他组过大；Full-1-6的最大值与最小值相对其他组较小；Full-1-5的最大值相对其他组过大，RMS值相对较小，Full-1-3的RMS值相对较大。初步可将1-1、1-5、1-6、1-7筛除。

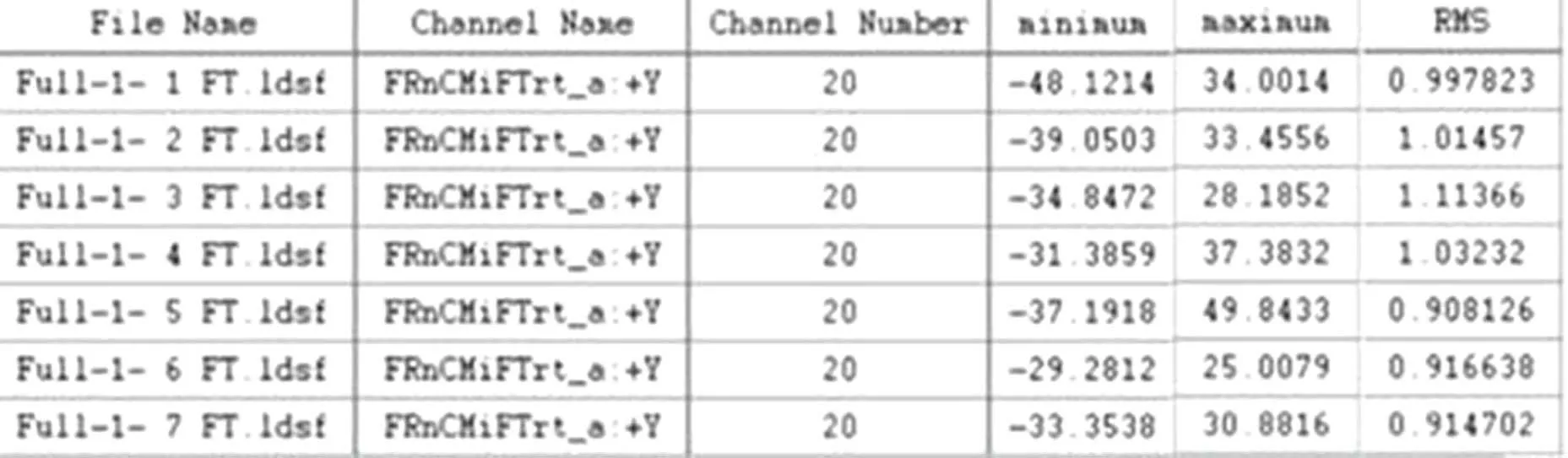
图5 载荷谱统计学指标Fig.5 Load spectrum statistic index

3.3 消除奇异值

在路谱采集过程中，由于采集信号链的电子元器件干扰、采集线路上的非正常冲击等因素，会造成采集到的载荷谱出现异常的高频信号点，一般称为奇异值，也称毛刺（如图6所示）。奇异值是幅值极大、具有随机性的高频信号。该信号会在很大程度上影响道路模拟试验的精度。

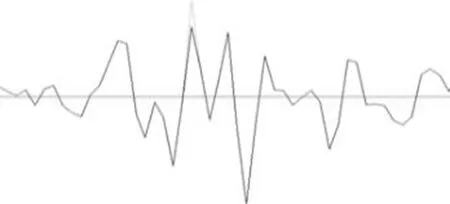
图6 奇异值

奇异值常用莱茵达准则进行判定[10]：对于采集的数据列x1,x2,x3,…,xn，先求得算术平方根：再根据贝塞尔法求得均方根偏差：σ=时，则xi为粗大误差，应剔除；若为正常数值，予以保留。k≥3，取值根据由小到大保证删除点较少的原则而定[11]。在3.2节筛选剩下的路谱中，再将奇异值较多的进行进一步筛除。

3.4 消除趋势项

趋势项亦成为漂移（如图7所示，采集到的载荷历程偏离了零线）是信号整体上的一个异常倾向，一般由于信号的采集、测量、传输过程的各种因素导致。一般可通过商业软件修正。将经过3.1至3.3筛选剩下的路谱，最后再将趋势项较为严重的筛除，可选出最优的1～2组进行下一步使用。

图7 趋势项Fig.7 Trend term

3.5 道路载荷谱编辑

载荷谱的编辑关系到能否进行准确且合理的室内加速试验。故进行载荷谱编辑时，应满足以下要求：编辑前后应保持损伤相差不超过95%；编辑前后应保证相位同步，即同一文件名下的所有通道应同步编辑；编辑后的信号应满足台架迭代需求。

该项目中基于等损伤的原则实现道路载荷谱的编辑。对采集到的载荷谱，进行时域分析，辨识出特征路段（如坑洼路、甲乙种水泥路面、搓板路等），将特征路段之间的过渡路段减去，不仅实现了载荷谱压缩，也保留了车辆的运动姿态，如图8所示。由图8 b中的横坐标也可看出，编辑前后损伤的差值非常小，满足要求。

3.6 傅里叶低通滤波

由于汽车产品在使用过程中一般只受到0～40 Hz低频载荷的作用，故需对采集到的载荷谱进行傅里叶低通滤波。道路载荷谱是时间序列，通过傅氏变换将原信号转换到频域，再与滤波函数相乘实现滤波[12]。滤波完成后，进行傅里叶逆变换，便可得到滤波后的时域信号。由图9可看出，滤波后的信号只含有0～40 Hz的频率成分了。

4 室内道路模拟试验台搭建

试验模型包括待测系统与测试系统。首先待测系统的确定，直接关系到待测模型的外观尺寸与工装安装位置、安装形式和作动缸的加载位置。

图8 载荷谱编辑Fig.8 Load spectrum edit: a) time-domain signal edit; b) damage comparison before and after edit

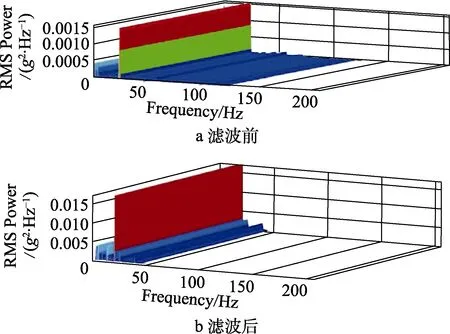
图9 低通滤波Fig.9 Low-pass filtering: a) before filtering;b) after filtering

4.1 试验模型的确定

该项目待测系统包括蓄电池系统、双油箱系统、空滤器系统。由于待测系统在车架上布置较为分散，车架前中后部分都有待测样件，因此本次项目采用整车级道路模拟试验，即保留整个车架进行试验，如图10所示。

图10 七轴试验系统总观Fig.10 7 axel test bench test system

4.2 试验系统基本参数

试验模型确认后，车架在整车状态受力形式主要集中于前轴与平衡轴，同时考虑到复现六自由度所需通道数量。作动缸布置形式可以确认：垂向四个作动缸，可实现垂直方向位移；横向两个作动缸可实现横向位移；一个纵向作动缸，可实现纵向位移；三个方向作动器结合可实现滚转、俯仰、偏航。

七轴液压伺服振动试验台主体由七个作动器和液压伺服控制系统构成，对设备有以下要求。

1）作动器伸长量：z向作动器：≥110 mm；y向作动器：≥125 mm；x向作动器：≥125 mm。

2）作动器推力：z向作动器：≥10 t；y向作动器：≥2.5 t；x向作动器：≥2.5 t。

3）自由度：纵向、横向、垂直、滚转、俯仰、偏航。

液压伺服控制系统（如图11所示）由分油器、蓄能器、二级阀、三级阀、位移传感器、力传感器、控制器和 RPC控制软件共同组成。该系统可通过计算机实现对信号的编辑、分析生成控制指令信号。控制系统可将指令信号转换为电信号，伺服系统可将电信号转换为液压油的流量及压力。最终作动缸将液压油的流量与压力转化为机械运动并反馈至电控系统，电控系统通过多重闭环严格控制执行机构。

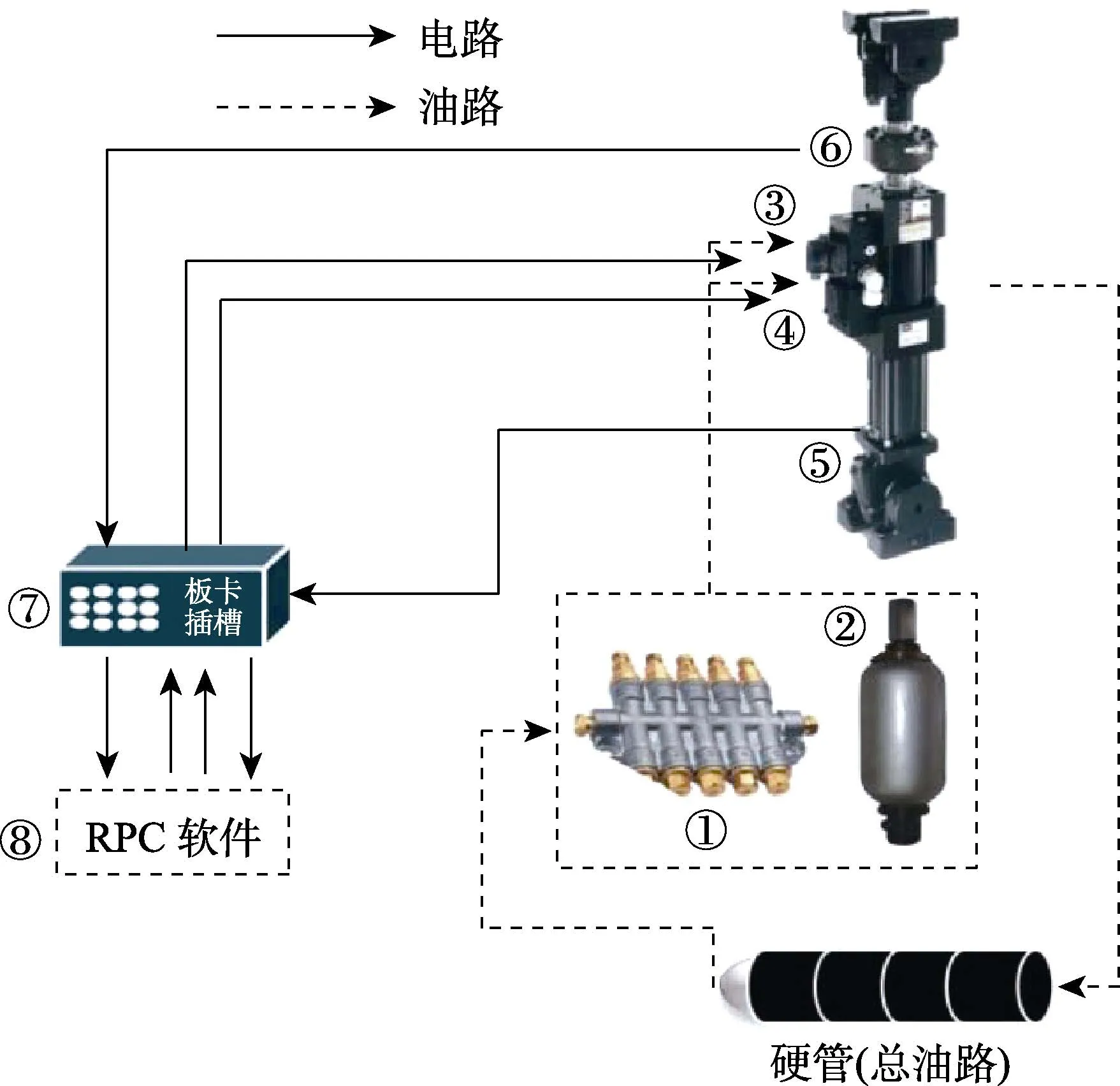
图11 液压伺服控制系统Fig.11 Hydraulic servo control system

4.3 自由度校核

确定工装及作动缸与车架的连接形式后，根据不同连接副的约束数对整个试验系统的自由度进行计算：

式中：n为空间机构构件数目；F为空间机构的自由度数；i为运动副；pi为运动副级数。

根据试验模型计算结果，系统16个剩余自由度中包括3个局部自由度及7个原动件，其余6个为车架的自由度。原动件数目应小于整个系统的自由度，符合试验要求。试验台工装如图12所示。

图12 七通道道路模拟试验台工装形式Fig.12 Frock clamp form of bench test

5 虚拟迭代与结构动力学修正

台架试验的模型与整车的模型始终无法保证一致，即在质量、刚度、阻尼上存在差异。该项目为多系统携带模态振型的同时验证，试验过程中需要保证激励与响应与实车一致，模型的不一致会给后续迭代工作带来困难。故在正式物理试验开展之前，根据虚拟迭代的结果，通过多体动力学软件进行模型修改，实现迭代结果的改善。

5.1 多体动力学分析原理

该项目的多体动力学分析是基于Admas软件的，在 Adams多体动力学软件建立虚拟样机模型时，首先是将所建模型的基本尺寸参数输入软件中，软件后台的求解器将自动建立起系统的拉格朗日运动学方程，并且同时建立起各个组成部件广义坐标系下的六阶微分方程，同时建立起系统各个组成部件的约束方程[17]。

5.2 虚拟迭代应用

当准确的动力学模型建立完毕后，将模型输入至Femfet.lab中就可以进行基于采集好的载荷谱的虚拟迭代了。与物理迭代的原理与步骤一样，以第一章中收取的道路载荷谱为目标信号，选取物理试验所需的七个通道进行迭代。虚拟迭代信号与路谱实测信号的比较包括2个方面：RMS error与损伤值。由图13可看出，各通道RMS error 均可控制在15%以下。

图13 虚拟迭代结果Fig.13 Virtual iteration result: a) resonance road A;b) washboard road A

5.3 响应信号的载荷提取

完成虚拟迭代后，以虚拟迭代完成的驱动信号对模型施加激励，提取待测样件油箱、空滤器、电瓶箱上的响应加速度信号。对比提取的信号和实际车辆采集的响应信号，通过不断调整台架试验模型的质量、刚度使所有待测样件的提取信号与实际采集信号接近。模型的修改原理主要基于式（7）：

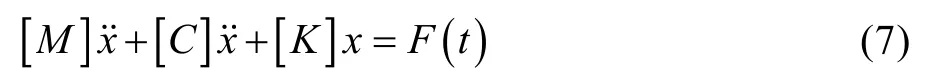
式中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；F(t)为外界激励；x为系统位移。

通过多轮次的迭代，对比各响应点的信号，最终建议在平衡轴中心线处添加一个横梁以增加整个试验模型的刚度。模型更改后，在甲乙种水泥路上，油箱上的迭代信号与实采信号对比如图14所示。可以看出，整体趋势几乎一致，也没有明显的相位差，符合试验要求。

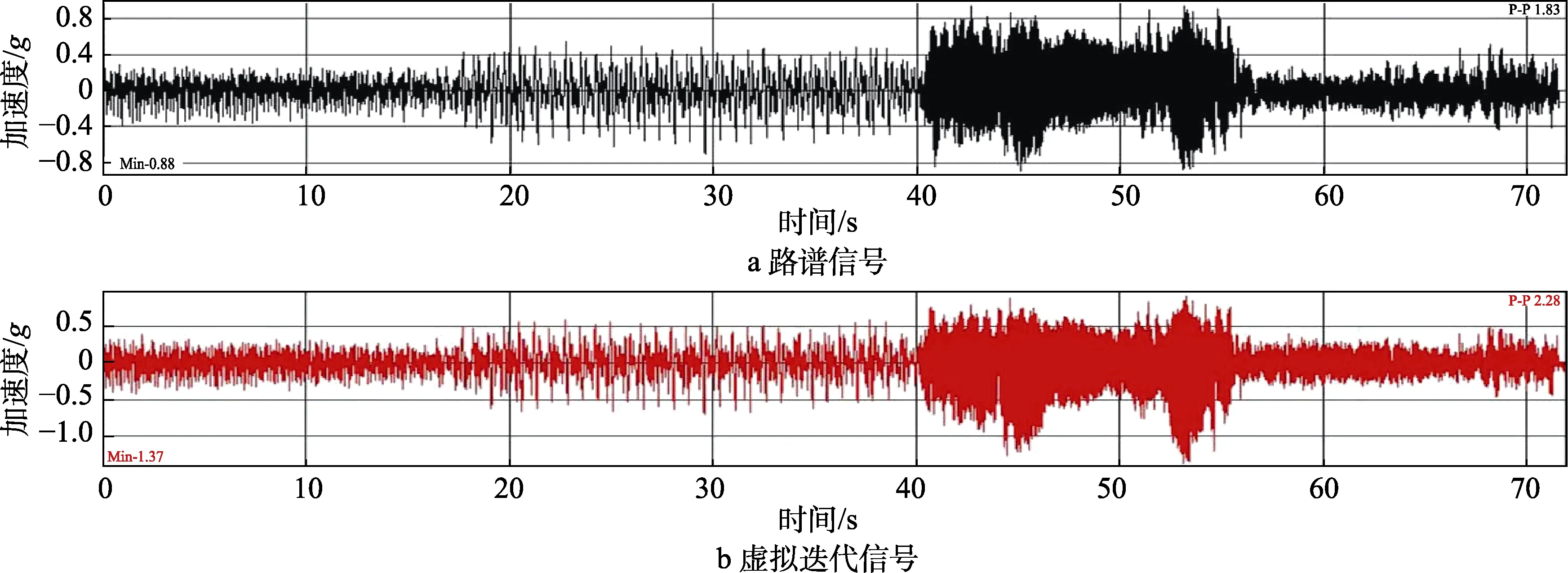
图14 路谱信号与虚拟迭代信号对比Fig.14 Load spectrum (a) and virtual iteration signal (b) comparison

5.4 驱动信号的对比

通过虚拟迭代，可实现输出七个激励施加点的位移信号，与之对应的是物理台架的作动缸施加点的激励。下面对坑洼路虚拟迭代出的驱动信号与台架实际物理迭代信号进行对比，其他路段不在此一一列举，由图15可看出，虚拟迭代驱动信号与实际物理台架迭代的驱动信号在时域上有很好的重合度，整体走向与统计学特性是基本一致的。

图15 甲种水泥路驱动信号对比Fig.15 Drive Signal Comparison in Resonance Road A

6 多通道道路模拟试验

为了重现车辆在试验场的加速度历程，需要通过系统计算过程反推出试验台作动缸对迭代点的驱动信号。一般道路模拟试验分为系统识别与道路模拟迭代两个过程，其中系统识别对后续迭代结果精度有着重要的影响[13-14]。

6.1 迭代点准备

根据整车的受力形式，选取前轴中心线，平衡轴中心线处车架上端面，4个z向加速度和2个y向加速度，以及车架前端1个x向加速度共7个通道为迭代通道。油箱、电瓶箱、空滤器上的通道为监控点。

6.2 试验系统识别技术

试验系统识别技术即频响函数识别技术，频响函数矩阵的精准识别是进行迭代的基础。与模态参数识别方法一致，试验系统识别技术分为单点激振法与多点激振法。

单点激振包括单点激振单点响应（SISO）和单点激振多点响应（SIMO），常用SIMO方法进行系统识别，算法上利用H1估计模型。通过对每个激振点施加激励，拾取各控制点响应从而获取整个频响函数矩阵。单点激振一次可以识别出频响函数矩阵的一列，其优点是便于控制激励信号的能量，噪声信号水平低，对样件损伤较小。缺点是识别周期较长，频响函数识别精度不高。[15]

多点激振即多点激励多点响应（MIMO），同时对所有的激振通道，算法上使用Hv频响函数识别算法，一次激振可以得到整个7×7频响函数矩阵。多点激振的优点是能量分布均匀，识别精度较高。缺点是对样件损伤较大，同时当频响函数识别出现问题时，不便于反查。

6.3 频响函数矩阵识别算法

对于频率函数矩阵识别算法，理想的模型如图16所示。

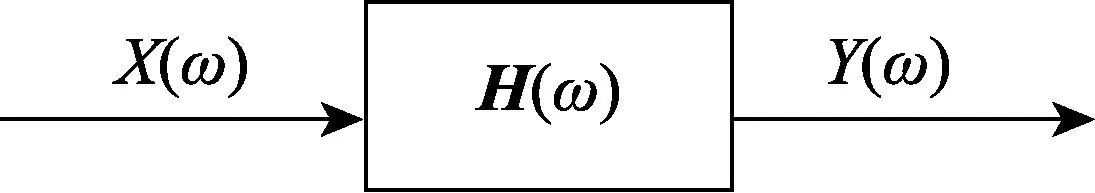
图16 频率函数矩阵识别算法理想模型Fig.16 Ideal model of frequency function matrix identification algorithm

图16中，Y(ω)为测量响应y(f)的频域信号；X(ω)为激励x(t)的频域信号；H(ω)为待测系统的频响函数矩阵。

一般测量误差按照出现规律可分为系统误差、渐变误差、随机误差与粗大误差[16]。随机误差是没有任何规律的，故假设在频响函数矩阵识别的时候至少存在随机误差。该项目中使用单点激振法，算法上为H1法，其模型如图17所示[12]。

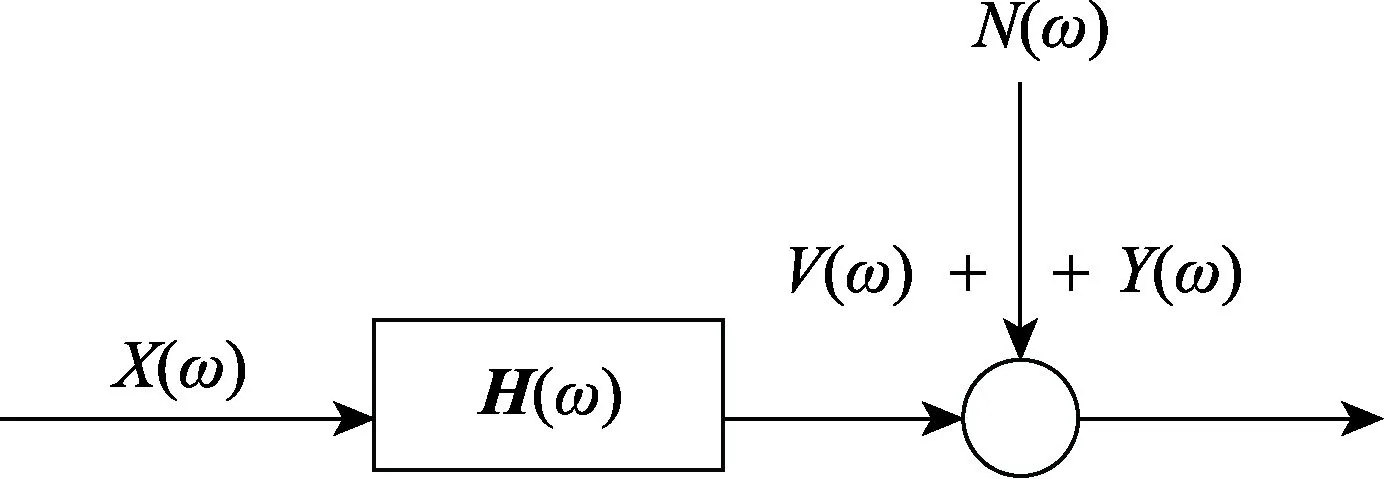
图17 H1法模型Fig.17 H1 model

图17中，Y(ω)为测量响应y(f)的频域信号；X(ω)为激励x(t)的频域信号；H(ω)为待测系统的频响函数矩阵；N(ω)为输出误差的频域信号。

对于待测系统，在既定的频率下，X(ω)与Y(ω)已知，图17所示模型为线性模型，因此求解频响函数矩阵就变为一个线性估计问题。即使用了最小二乘法：所选择的回归模型应该使所有观察值的残差平方和达到最小。

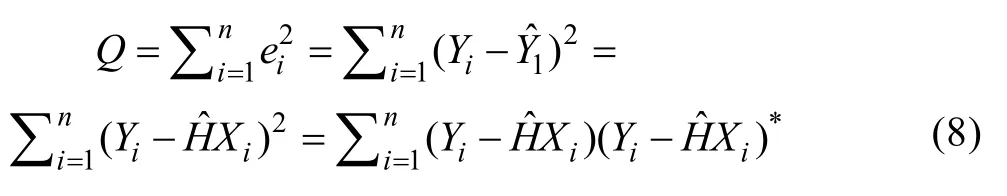
将Q对 ˆ*H求偏倒数，并使其为0，即可得为输出与输入的单边互谱密度；Gxx为输入的单边自功率谱密度系统识别的质量，一般由相干函数来评判，相干函数越接近1，识别的质量越高。

6.4 初始驱动信号的产生

在已知期望信号Y0(f)并完成频响函数矩阵识别后，可求得初始驱动信号X0(f)。

式中：H－1为频响函数。对式（11）进行逆傅里叶变换，可得时域下初始驱动信号X0(t)[18]：

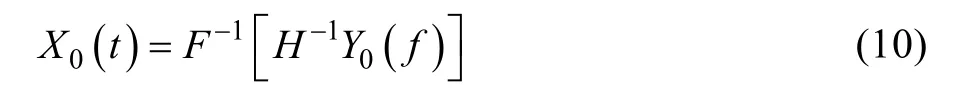
6.5 多轴向多激励迭代原理[15]

首次迭代后，误差信号ΔY为期望响应信号与首次迭代后的实际响应之差：

若 ΔY(f)不满足试验精度要求，需对驱动信号进行修正：

则理论上的时域修正量为：

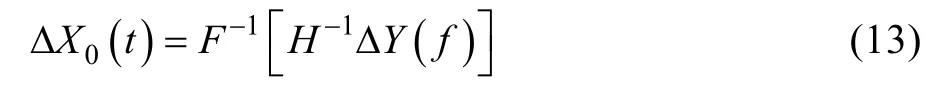
进而获取新一轮迭代的驱动信号：

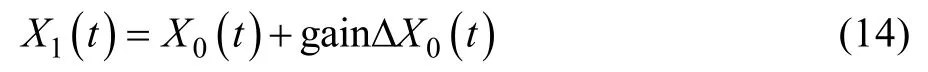
式中 gain为增益系数，由新的驱动信号进行激励，从而得到新的响应信号，再进行修正，如此周而往复，直到误差信号的均方根误差与期望信号的均方根误差满足试验要求。迭代流程如图18所示。

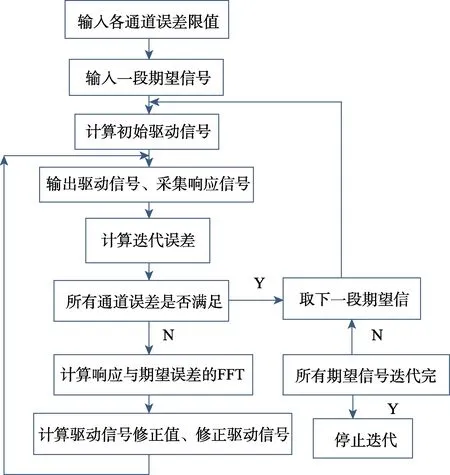
图18 迭代流程Fig.18 Iterative process

6.6 迭代质量评价

以均值、最大值、最小值及均方根误差值等统计学特性为统计项目，将迭代点信号与期望信号在幅值域对比。通常要求各迭代点与期望信号的均方根误差值控制在20%以内，视为迭代质量较高。

迭代完成后，应比对各通道的迭代响应信号与期望信号的自功率谱密度，应保证两者能量分布在各频段基本一致。各通道的损伤值、迭代响应信号与期望响应信号的损伤值相差应在10%以内，可视为迭代较为成功，该拟合度在可以接受的范围。

6.7 耐久试验

迭代完成后，就可按照设定好的程序进行室内耐久试验。根据不同产品的耐久要求，需要在控制软件中输入循环次数。3.1中提及的11种路段全部跑完一遍为一个完整循环，本项目油箱要求完成2500循环不出现疲劳问题，故试验总时间为所有路段编辑后路谱时域信号的长度相加再乘以 2500。试验前在各关键零部件安装位置螺栓上进行标记，试验中每隔2 h进行一次检查，观测各安装处螺栓力矩是否有衰减，各待测零部件表面是否有裂纹等。

7 结语

该项目针对多系统的“整车级”道路模拟试验过程中出现的迭代不收敛的问题提出了技术路线与解决方法。通过前期的模态分析，制定出了合理的路谱采集方案，同时通过虚拟迭代技术修正了台架试验的模型，最终在油箱上的通道迭代过程中取得了良好的效果（均方根误差＜15%)。与此同时，该项目也存在着一定的不足与缺陷，受限于虚拟迭代的工作量以及液压伺服系统的限制，空滤器系统没有到达预想的迭代准确度。

最后，该方法实现了结合多体动力学仿真、模态与疲劳分析、基于液压伺服七轴试验台物理验证的联合验证形式，也涉及了模态分析、疲劳耐久理论、数字信号分析理论、结构动力学理论多门学科，为现代验证技术的典型代表。同时也为后续虚拟台架的研究奠定了良好的基础。