基于路谱的随机振动耐久试验研究

段凯欣，胡玉倩，刘瑜瑾，张凯

（北京福田戴姆勒汽车有限公司，北京 101400）

结合北京福田戴姆勒汽车有限公司发动机排气管新产品开发项目，进行整车级道路模拟试验的研究，提出整体解决方案。围绕台架关联试验场坏路，基于累积损伤模型、雨流计数法和危险截面损伤分析、色谱分析、疲劳损伤谱分析、冲击响应谱分析展开研究，通过道路载荷谱的采集、预处理、色谱分析、危险点危险截面分析、道路冲击响应谱、疲劳损伤谱和台架冲击响应谱、疲劳损伤谱对比分析，最终使产品在台架试验危险点和危险截面的位置、角度、损伤与道路试验保持一致，达到合理验证产品耐久性的目的。主要解决了多轴疲劳无法转化单轴疲劳、发动机振动激励和路面振动激励同时复现困难、路谱时序信号加载成本高周期长、正弦振动信号频率无法和道路载荷信号关联等疑难问题。建立了车辆道路时序信号与模拟试验台架加载谱的相关性转化映射关系，执行了基于电磁振动试验台的单轴耐久试验，并形成多轴耐久转化为单轴耐久试验的分析方法。

1 随机振动耐久试验理论

1.1 适用范围

该试验方法多用于考核汽车电子电器产品耐久性。

1.2 位移响应谱

将路谱信号按照特征路段截开，保证每段信号是宽带平稳随机过程。将n自由度系统转化为n个单自由度（SDOF）系统，如图1所示。利用杜哈梅积分公式，将加速度激励信号转化为n个单自由度系统相对位移冲击响应信号。

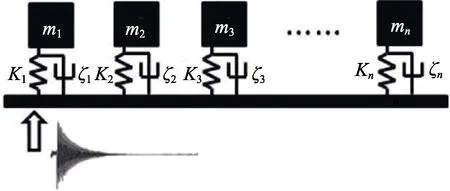
图1 n个单自由度（SDOF）系统Fig.1 n SDOF systems

受随时间变化的外载F(t)和黏性阻尼作用下的线性单自由度（SDOF）系统的运动方程是一个二阶常微分方程。

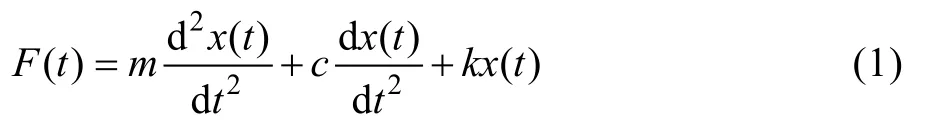
式中：m为等效振子的质量；x为系统振幅；t为时间；c为黏性阻尼系数；k为系统刚度。

单位脉冲响应函数，如公式（2）所示：

式中：ωd为系统在当前存在的阻尼c作用下的实际振动圆频率，为系统在无阻尼状态下振动的固有圆频率；ζ为系统的阻尼比，。

推广到任意时刻τ的单位脉冲响应函数，如公式（3）所示：

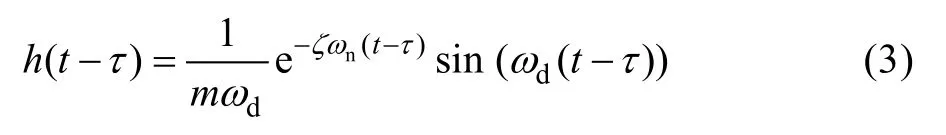
阻尼比在0～1之间的n个单自由度（SDOF）系统的位移响应x(t)是时域信号a(t)和推广到任意时刻τ的单位脉冲响应函数的卷积，即杜哈梅积分形式，如公式（4）所示。

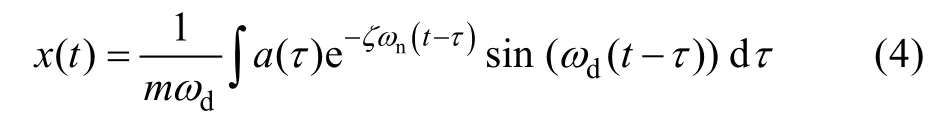
通过公式可以计算线性系统以a(t)为激励，在ω0下产生冲击响应的相对位移时域信号。可以通过卷积在不同ω0下的冲击响应谱，得到在不同ω0下产生冲击响应的相对位移时域信号。

1.3 移除毛刺

分辨路谱中的异常波峰和波谷如图2所示，应将异常波峰、波谷移除[1]。

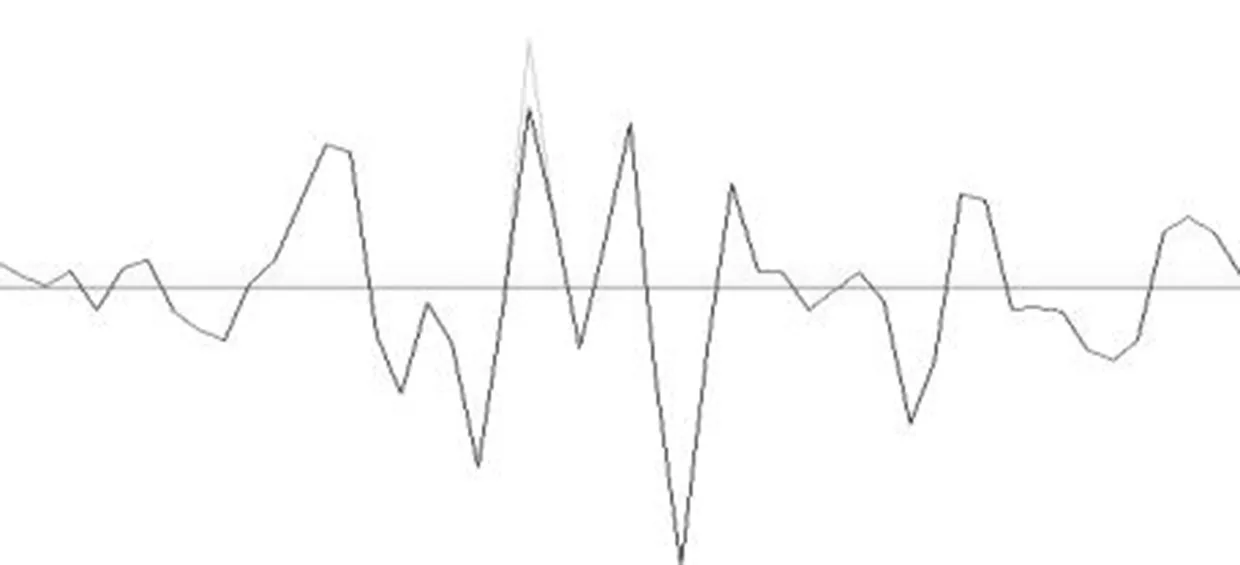
图2 毛刺移除Fig.2 Burr removal

移除量按公式（5）计算[2]，计数 1个毛刺的构成点数N，取3×3×N个点，计算其均值u1。

式中：Xi为时域信号中以毛刺波峰或波谷为中心3×3×N个点的纵坐标。

取3×N个点，求3×N个点的偏移量均值u2：

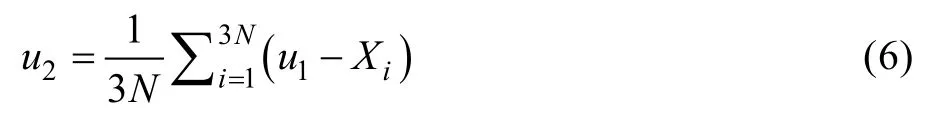
求移除量G，如公式（7）所示。

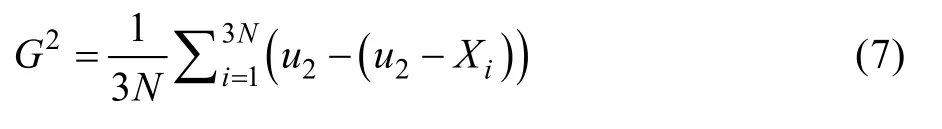
1.4 移除奇异点

对于信号本身不连续的时域段和信号一阶导数不连续的时域段，需要移除。

1.5 漂移修正

对于零线明显上偏的情况，需要进行零线修正，将零线偏移至整段路谱均值处。

1.6 疲劳损伤谱（FDS）

分析频带带宽通常为5～2000 Hz时，依据宽带、平稳、随机原则将路谱分段，每段需要卷积分析频率ω0从5～2000 Hz的单位冲击响应信号，分别得到1996个时域信号。如图3所示，每段按上述步骤处理，每段分别得到1996个时域信号。

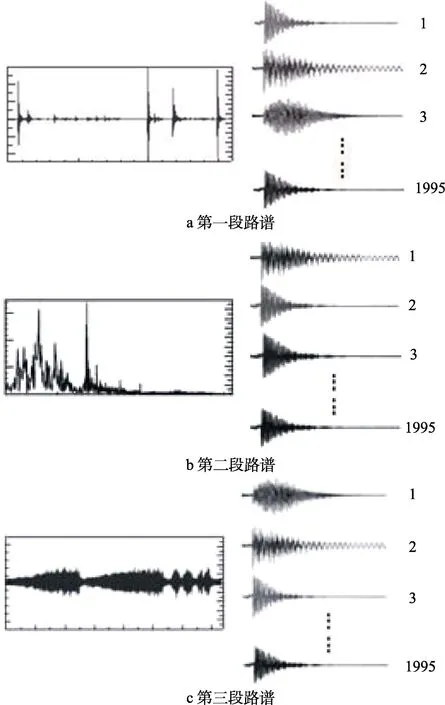
图3 各态历经路谱卷积各个频段的路谱Fig.3 Ergodicity road spectrum convolution integral in each frequency band: a) section I of road spectrum; b) section II of road spectrum; c) section III of road spectrum

将滤波后的时域信号分别进行雨流计数[3]，先将时域信号纵坐标划分 bin，以达到简化计数的目的。bin的个数建议划分为10倍纵坐标最大值，最高值建议设定为纵坐标最大值的5%。划分bin处理路谱的方法如图4所示，将采集点移至其所在 bin区的中间，然后仅依次连接最高点和最低点，生成新的时域信号。

图4 划分bin的简化计算法Fig.4 Simplified calculation method of dividing bin

以四点计数法为雨流计数的计数原则[4]，通过古德曼等寿命曲线进行平均应力修正。当试样存在缺口或倒角时，计算损伤时需要进行集中应力修正。应力集中系数Kt[5]是集中应力和名义应力的比值，可以修正S-N曲线。

最后通过 Miner Rule[6]线性损伤模型来计算损伤值。

1.7 冲击响应谱（SRS）

由于路谱按照宽带、平稳、随机原则将路谱分段，每段按照杜哈梅积分处理后，每段卷积分析频率ω0从5～2000 Hz的单位冲击响应信号，分别得到1996个时域信号。按照图5把ω0作为频域信号的横坐标，卷积相应ω0后形成的时域信号的极大值作为频域信号纵坐标，能形成该段激励信号产生的冲击响应谱。分别求出每段冲击响应谱，每段冲击响应谱相同横坐标取最大值，可以求得整段路谱的冲击响应谱。

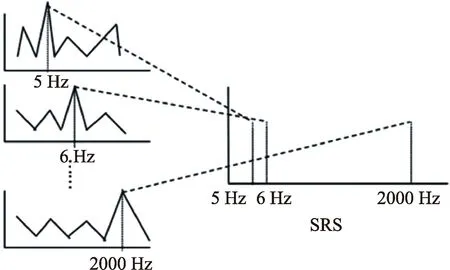
图5 SRS生成Fig.5 SRS generation

1.8 冲击响应信号功率谱密度（PSD）

通过公式建立FDS、耐久试验时间t和功率谱密度PSD的关系。通过目标路谱的FDS确定目标损伤值，设定耐久试验时间t，随机振动功率谱密度PSD将是唯一未知数。求解即可，如公式（8）所示：

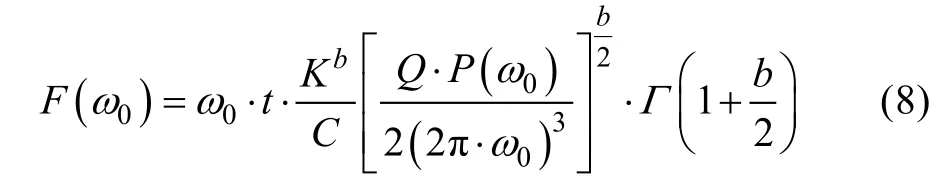
式中：F(ω0)为每段各态历经性时域信号卷积ω0后得到的冲击响应谱通过四点法、miner模型以及损伤修正方法计算出的损伤叠加值；t为振动耐久试验时间；C、b为 Basquin方程参数C=NSb参数，（C为疲劳耐久系数，N为应力幅值S的循环次数，b为疲劳耐久指数）；K为单自由度（SDOF）系统弹簧刚度系数；P(ω0)为频率ω0对应的功率谱密度；Q是动态幅值参数，（ζ为阻尼系数，通常取5%）；Γ(1+b/2)为 Gamma 函数，。

FDS生成的PSD通过平直化处理，将成为随机振动的输入。以ω0为冲击响应频率的单自由度系统，用加速度响应均方根值和位移响应均方根值表示PSD整体程度，达到定量评价PSD的目的。

1.9 极限响应谱（ERS）

FDS生成的PSD通过平直化处理，将成为随机振动的输入。通过公式（9），可以由P(ω0)和振动耐久试验时间t计算极限响应谱。ERS与SRS类似，表示以ω0为冲击响应频率的单自由度系统的P(ω0)对应的加速度或相对位移极大值。在1978年，lalane针对窄带单自由度（SDOF）系统提炼 Miles方程，提出并证明了公式（10），该公式被称为极限响应谱（ERS）或最大响应谱（MRS）。

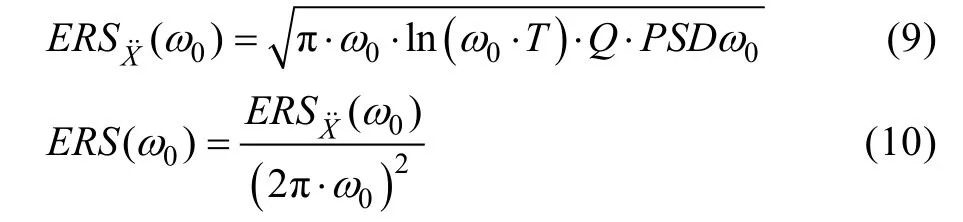
式中：ERS(ω0)和ERS(ω0)分别是以0ω为冲击响应频率的单自由度加速度极限响应值和位移极限响应值。

1.10 振动耐久试验频率分析

路面激励分析频率为0～80 Hz，根据采样定理，采样频率应为160 Hz。由于计算机识别二进制数制，A/D转换位数为2n，控制系统的分辨率为量程/位数，选择2.56的倍数，可以减少分辨率小数点后的位数，系统通常会保留小数点后一定位数，四舍五入进行显示。因此选择204.8作为采样频率，为进一步降低系统误差，选择256 Hz为采样频率。

传动系统激励分析频率以发动机点火频率为基频，其余旋转构件引起的振动激励为谐频进行分析。发动机怠速是600 r/min，分析转速1800 r/min的四冲程六缸发动机点火频率为3阶，因此分析频率范围为30～90 Hz，30齿的变速箱齿轮振动谐频为 300～900 Hz，可以选择2048 Hz为采样频率。

2 排气管振动耐久试验

以排气管的振动耐久试验为例，介绍随机振动试验流程。重点在于什么情况下多轴振动可以转为单轴振动，如何转化，以及与发动机相连时，如何确定定频冲击的激励源阶次和定频频率。

2.1 道路载荷谱采集

由于与发动机连接，排气管受到的激励主要来自于发动机和路面，采集来自发动机和路面的激励，将两个加速度传感器分别布置于发动机缸盖和近排气管末端的车架平面上，采集路面载荷谱。由完整路面载荷谱发现，发动机端传感器加速度幅值远大于车架端（如图6所示），排气管所受激励主要来自于发动机，且对比实际不同特征路面采集时间及车架端路面载荷谱观察，发动机端路面载荷谱不具有受到特征路面影响的现象。

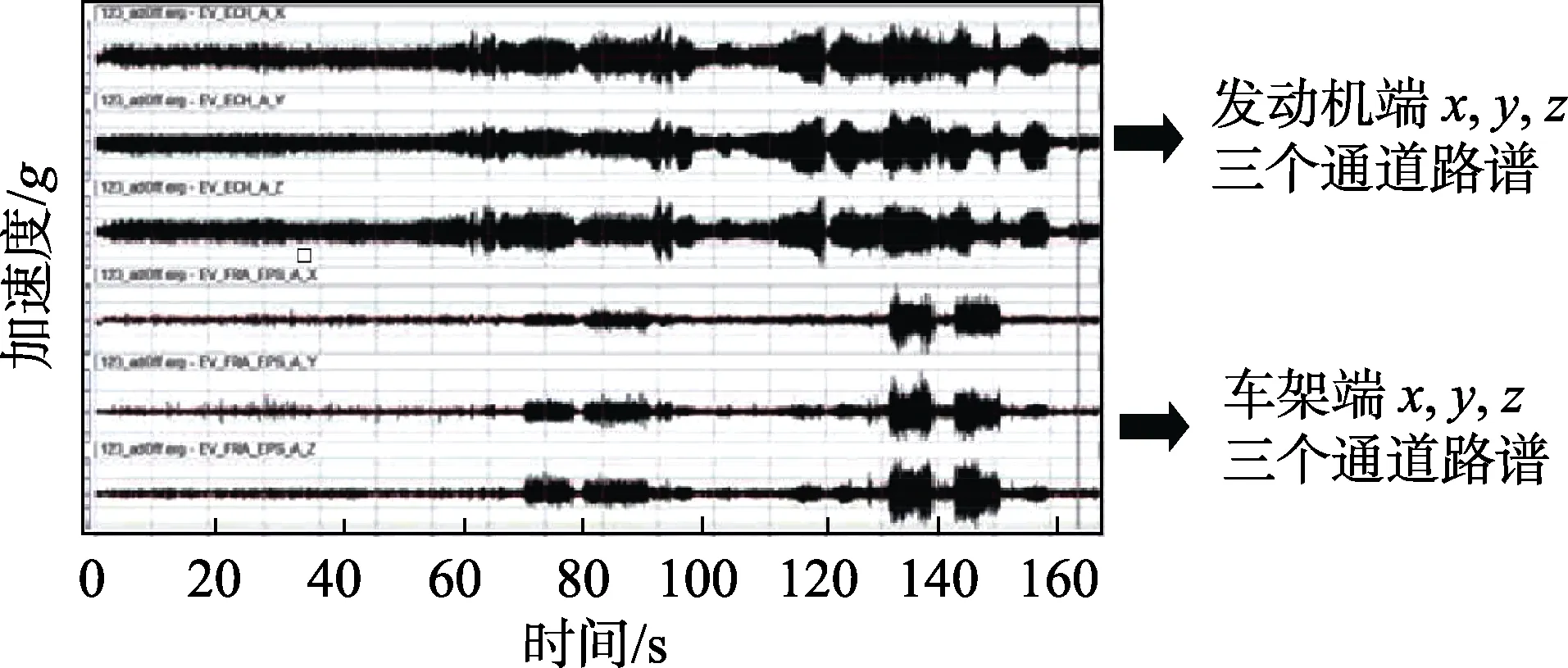
图6 发动机端和车架端路谱Fig.6 Road spectra of engine end and frame end

2.2 多轴转单轴

采用发动机端原始完整加速度数据进行分析，通过CriticalPlane方法，对排气管数模进行仿真模拟分析。通过计算危险点、危险截面，分别比较单个x/y/z通道危险截面角度与整车三通道危险截面角度是否接近，损伤值相差多少倍。分析结果（如图7和图8所示）显示，只有z通道危险点、危险截面与三通道危险截面角度一致，损伤值仅相差20倍，而x、y通道与三通道损伤值相差几个数量级，故判定z方向为排气管主要激振方向。该排气管振动试验可简化为z向单轴振动试验。因为该道路载荷谱波形杂乱，随时间的变化不具有一定规律，无法用确定性函数表示，故采用随机振动的试验方法。由于三通道损伤值是z向通道损伤值的20倍左右，所以进行z向单轴振动时，最终耐久试验时间要考虑损伤值的倍数。

图7 z通道危险点、危险截面角度与三通道危险截面角度Fig.7 z-channel critical point, critical plane angle and 3-channel critical plane angle

图8 z通道危险点损伤值与三通道危险点损伤值Fig.8 Damage of z-channel critical point and 3-channel critical

2.3 确定定频频率及加速度幅值

由于与发动机相连，发动机内的旋转部件运转时，会产生一定幅值的响应，因此排气管会受到发动机内结构旋转件的影响。为了确定定频冲击激励源与定频频率，对原始完整加速度数据进行 colormap分析，进而得到瀑布图（waterfall），见图9和图10，可以得到主要激励源阶次，进而计算定频频率。

图9 瀑布图Fig.9 Waterfall

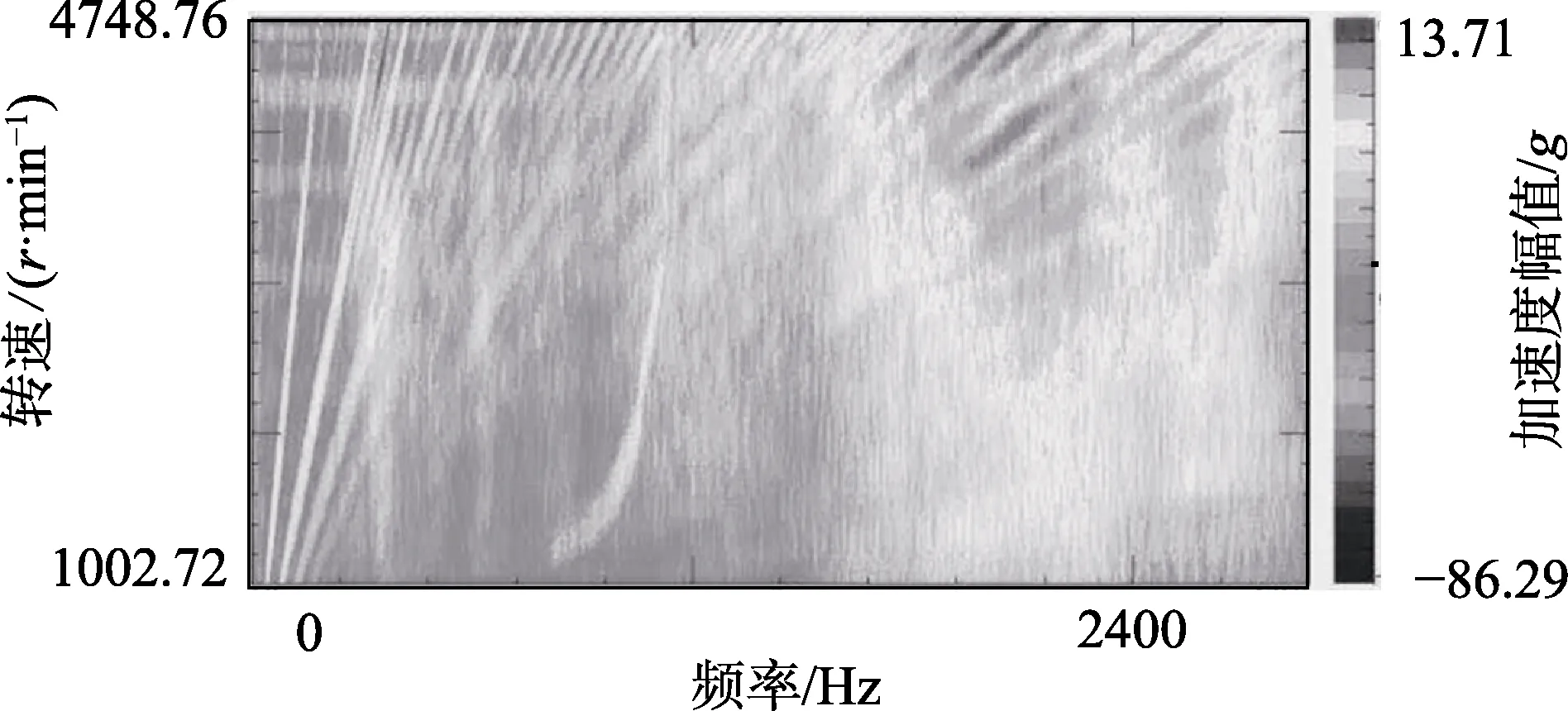
图10 色度谱Fig.10 Colormap

由于时域信号时间很长，一次傅里叶变换不足以将整个信号处理完，因此将时域信号按一定的时间将信号截断，对每段信号进行 FFT（Fast Fourier Transform）分析，进行一次 FFT分析所截取的时域信号长度为1帧或frame size。相邻两个时域数据点的采样时间差称为时间分辨率，等于采样频率的倒数，采集到的时域信号是离散的。同理，频谱也是离散的，相邻两条谱线的频率差称为频率分辨率。每次FFT计算采用固定长度的时域块，数据长度由频率分辨率决定，每块时域数据与下一块时域数据的时间间隔由步长决定。瀑布图分析可以采用跟踪转速的方式，跳跃的步长为等转速步长，而非等时间步长。FFT计算得到的结果只位于频率分辨率的整数倍处，也就是谱线处，谱线与谱线之间没有结果，频谱的这种离散效应称为栅栏效应。以等转速步长计算瞬时 FFT频谱，如转速步长为 10 r/min，则表示转速每变化10 r/min，计算一次瞬时频谱，每次FFT变换对应的时域数据长度为频率分辨率的倒数。每个数据块对应一个转速，然后按照转速的先后顺序将各个瞬时频谱排列得到三维瀑布图（waterfall），colormap图是瀑布图的平面形式，是用颜色冷暖来表示幅值的二维图。在瀑布图中可以看出，各频谱有间距，但在colormap中看不出间距。colormap图中颜色最亮的线即为最主要激励源，同时可以显示主要激励源阶次。

阶次是结构旋转件因旋转造成的振动和噪声的响应，阶次代表的是旋转一圈事件发生的次数。例如一个旋转轴上有齿轮盘，齿数为23，即齿轮啮合时，每旋转1周，齿轮碰撞发生23次，该齿轮的阶次数为23。进行colormap分析时，导入发动机转速与道路载荷谱，即视曲轴旋转为1阶1倍转速，分析主要激励源阶次为K阶K倍转速。转频即为转速的1/60。所以定频频率的计算公式为：定频频率=发动机常用转速/60*阶次。

为了确定定频冲击的加速度幅值，导入发动机端道路载荷谱，过滤出频率在89.5～90.5 Hz的道路载荷谱，去除异常毛刺点，取最大幅值即为定频冲击的加速度幅值。为了确定随机振动试验的频率范围，计算原始完整加速度数据的功率谱密度，观察功率谱密度曲线，选取幅值较大的曲线所在的频率范围，即为最小频率和最大频率的范围。

2.4 路谱处理

对路谱进行去除毛刺、移除奇异点、漂移修正等处理，根据各态历经性，将路谱截成平稳随机过程的各段。为了后期计算方便，考虑先对疑似可以组合为一段平稳随机过程的不同路谱段进行合并。视幅值大体相同，波形平稳相似的路段为疑似路谱。如何判定疑似路段是否可以组合，先算出不同路段的功率谱密度，比较同一频率下PSD幅值的变化趋势是否一致，一致则可以视为同一平稳随机过程，可以合并。合并后将两段路谱连接部分进行平滑（smooth）处理，以保证振动的平稳连贯性。

2.5 冲击响应谱（SRS）和疲劳损伤谱（FDS）的计算

以杜哈梅积分为运算原理，卷积各个频率下的单位冲击响应，计算并输出每段路谱的冲击响应谱和疲劳损伤谱。最小和最大频率（Minimum &Maximum Frequency）取决于原始路谱的PSD，路谱PSD幅值较大且有效的频率区间即为最小和最大频率区间。

循环圈数（Custom Repeat Count）：试验件要求寿命里程数/单圈有效里程数A、C、b指的是S-N曲线（以材料标准试件疲劳强度为纵坐标，以疲劳寿命的对数值l gN为横坐标，表示一定循环特征下标准试件的疲劳强度与疲劳寿命之间关系的曲线，称应力-寿命曲线，也称S-N曲线）中的系数。

由于各态历经性，将路谱截成若干段，因此会输出若干个SRS和FDS，分别计算SRS和FDS的总和，用求包络线的方法计算SRS，计算公式为max（test1，test2），用求和的方法计算 FDS，计算公式为（test1+test2）。输出总SRS和FDS。

2.6 随机振动试验条件确定

处理后得出总FDS，计算功率谱密度值。由于台架只能识别平直谱，故使用若干点的坐标来描绘PSD曲线，选点多一些为好，与 PSD曲线拟合得越接近越好，如图11所示。记录平直谱上点的坐标，将坐标点输入给试验台模块，计算ERS（Extreme Response Spectrum），可以输出随机振动试验的ERS和FDS。通过显示，将试验台模块计算出的ERS与原谱的SRS进行比较，如图12所示。同时将随机振动试验的FDS与原谱的FDS进行比较，如图13所示。

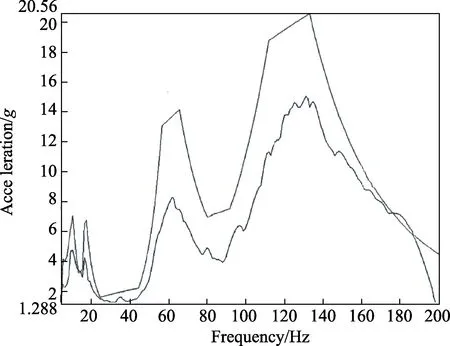
图12 随机振动ERS与路谱总SRSFig.12 SRS of random vibration ERS and road spectrum

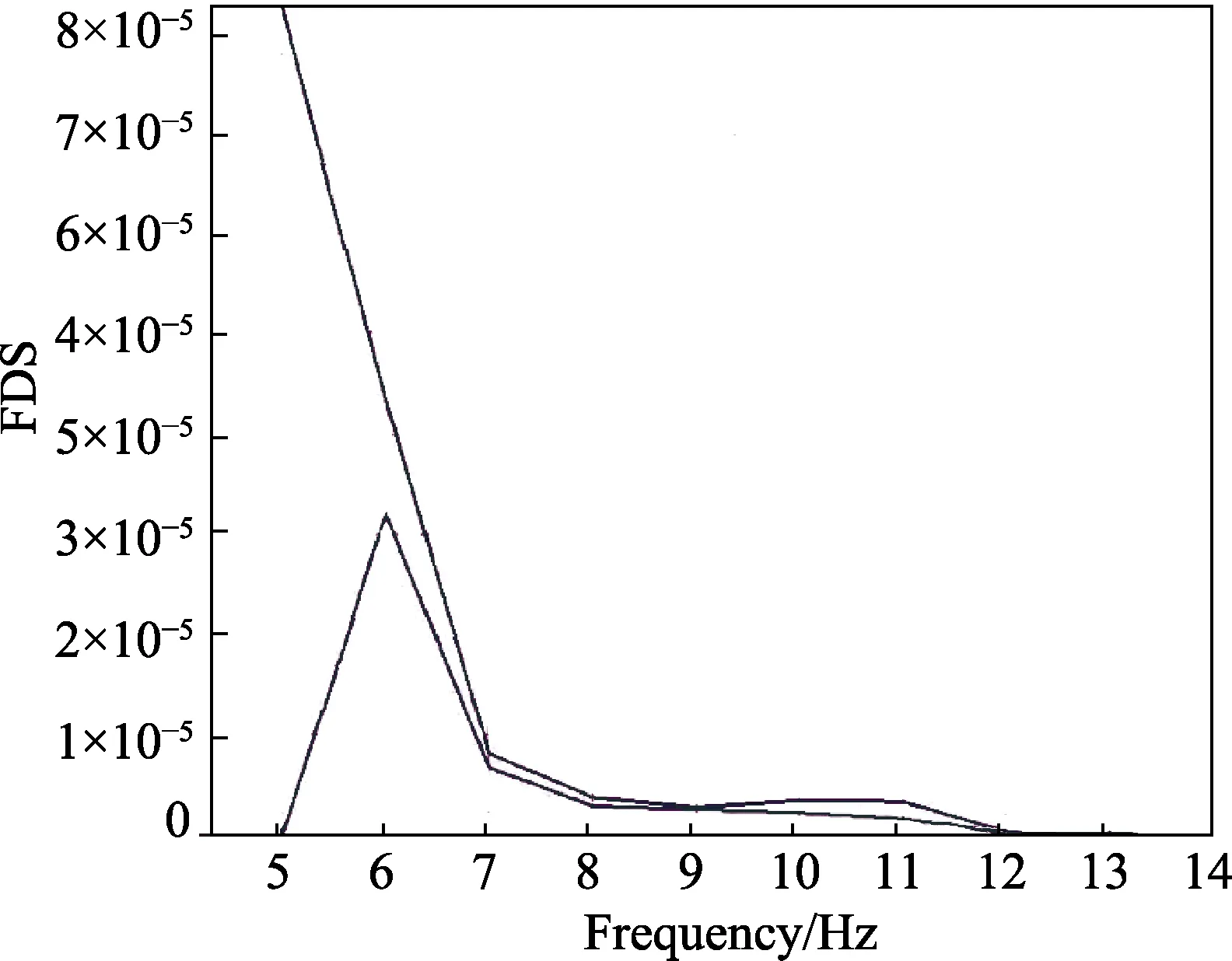
图13 随机振动FDS与路谱总FDSFig.13 PSD of random vibration FDS and road spectrum

将路谱总和的SRS和FDS与随机振动试验条件的ERS和FDS进行曲线比对。一般情况下，随机振动试验的ERS比较大，需要将原振动试验条件PSD平直谱中坐标点适当降低，以使随机振动 ERS与路谱总 SRS曲线拟合得越来越接近。但是随着随机振动PSD坐标点降低，其FDS也会降低。当低于路谱总 FDS时，可以通过调节试验时间来增大随机振动的FDS，但试验时间不宜调至过高，否则加速效果降低。总之通过调节随机振动 PSD坐标点及试验时间来使得图11、图12、图13中各曲线拟合程度达到最佳，此时便得到了随机振动试验的PSD及试验时间，确定了试验条件。

3 结语

通过上述的理论和过程，便可以将零部件的整车道路试验，在等损伤的前提下转化为台架振动耐久试验，从而实现了加速试验效果，缩短了试验周期，降低了验证成本。台架振动试验操作相对简便，试验环境良好，且试验过程便于监控。