汽车行驶诱发地表振动的解析研究1)
王立安 赵建昌 王作伟
(兰州交通大学土木工程学院,兰州 730070)
引言
随着我国城镇化进程的加速以及交通基础设施的大规模建设,很大程度上促进了社会经济发展,但也带来了诸多负面影响,例如噪声污染、环境振动等.交通网络的密集布置使得越来越多的民房和古建筑处于道路沿线,加剧了汽车行驶引起的振动危害.有鉴于此,深入研究汽车行驶诱发的环境振动响应,并给出可靠的预测模型显得极为重要.
近些年出现的文献中,关于轨道列车引起地基振动响应研究已有很多[1-6],而针对汽车载荷的地基振动响应研究却较少.最早研究汽车载荷引起地基振动,是将汽车载荷简化为移动点源或面源载荷进行研究[7-10],而这种简化是最理想的状态,没有考虑汽车悬架和轮胎的刚度、阻尼,以及地面状况对车--地相互作用的动态影响.Fryba[11]提出一种考虑汽车悬架和轮胎刚度、阻尼的两自由度1/4 汽车模型,该模型在后续研究中得到了广泛应用并取得大量成果.如:孙璐等[12]利用两自由度1/4 汽车模型分析了车--路动力相互作用;孙璐等[13]、黄新艺等[14]利用该模型分析了车--桥耦合振动响应;文献[15-19]同样利用1/4 车体模型对车--路面--地基系统的耦合振动响应做了研究.但值得注意的是,该模型尽管考虑了汽车悬架和轮胎的刚度、阻尼,但并未考虑轮胎在汽车行驶过程中的动态变形,将轮--地接触假设为点接触或接触面积恒定不变的面接触,这样的假设无法反映轮胎包容性对车--地相互作用的影响,而且上述研究中都只考虑了车--地之间的竖向作用,并未考虑轮--地之间的纵向滚动摩擦.孙加亮等[20]对近年来多柔体系统的动力学建模、分析方法以及相关成果做了系统总结和综述,并提出关于柔性部件动力分析的问题.郭孔辉等[21-24]在两自由度1/4 汽车模型的基础上考虑轮胎几何滤波效应和弹性滤波效应,提出反映轮胎包容性的弹性滚子接触模型,并做了实验验证.胡海岩[25]通过研究振动系统在状态空间中的可达流形后发现,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少半个自由度.刘志浩等[26-27]建立轮胎欧拉梁模型进一步分析了轮胎包容性对振动特性的影响.范纪华等[28]基于绝对节点坐标的弹性线方法对履带式车辆的动力学问题做了仿真分析.此外,也有学者采用现场实测的方法研究了汽车行驶诱发地面振动的特性,如叶茂等[29]、贾宝印等[30].但由于问题本身的复杂性且影响因素较多,实测方法未能得出有效的振动预测模型.
基于上述分析,本文在两自由度1/4 汽车模型的基础上结合郭孔辉[31]提出的弹性滚子接触模型,建立汽车与地基系统的耦合振动模型,并同时考虑车--地之间的竖向和纵向作用,利用Fourier 和Laplace 积分变换推导出地表振动位移的解析解.经过数值计算,系统分析了车速、地面不平度和轮胎包容性对地表振动的影响规律.
1 计算模型
图1 为1/4 汽车与地基相互作用的力学模型,车轮沿x方向以速度c匀速运动,o-x1为固定在车轮上的一维局部坐标系,方向平行于x轴,-r0≤x1≤r0,r0为轮胎半径.图中m1,m2为车身和车轮质量,z1=z1(t),z2=z2(t)为车身和车轮的竖向位移;z0=z0(t)为地面不平度(路形函数);K1,C1为汽车悬架刚度系数和阻尼,Kw,Cw为轮胎刚度系数和阻尼.2a,2b为轮胎着地长度和宽度,其中轮胎半宽b为常数,轮胎着地半长a=a(t)为随时间的变化量.本文着重反映汽车行驶载荷的激励特征,将地基考虑为均质弹性半空间.
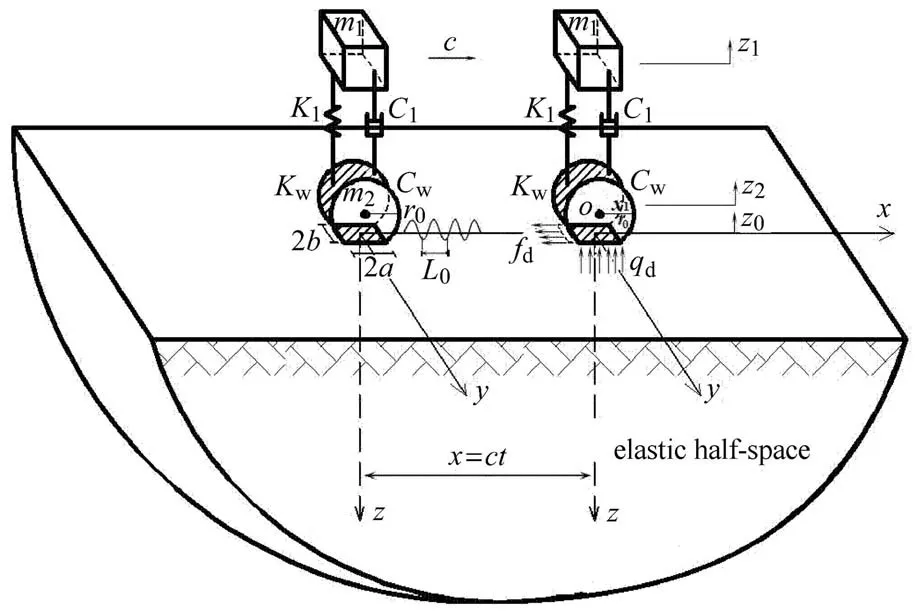
图1 模型示意图Fig.1 Diagram of calculation model
地面不平度z0(t)采用简谐波函数描述[24]

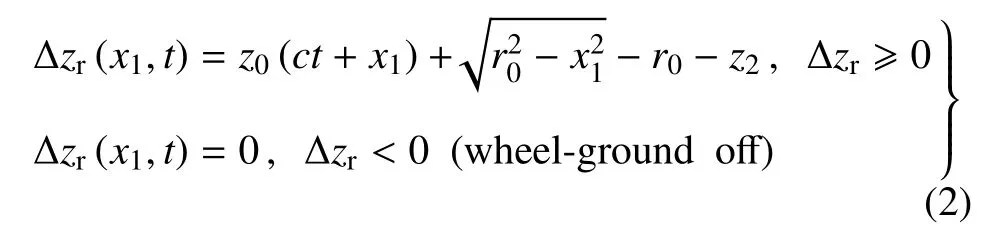
假设轮胎与地面间的接触力均匀分布,轮--地间的相互作用力可分别由下式表示.
竖向作用力
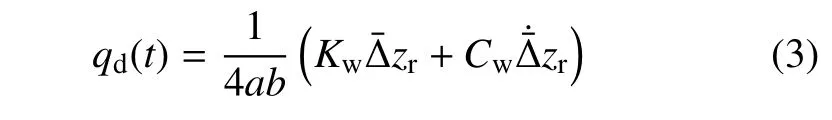
纵向摩擦力

2 问题求解
2.1 汽车系统动力方程及求解
根据D’alembert 原理,两自由度体系1/4 汽车系统的运动方程为

将式(7)、式(1)代入式(6),得到
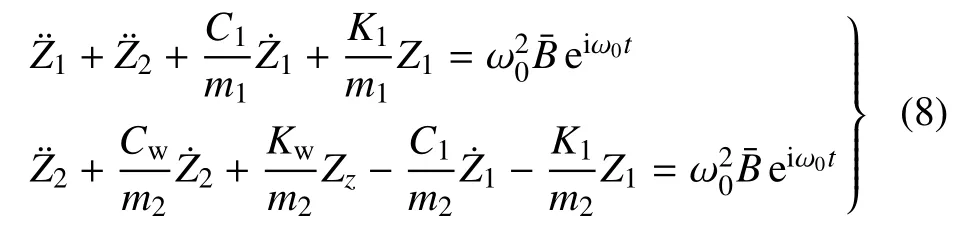
常微分方程组(8)的通解形式为
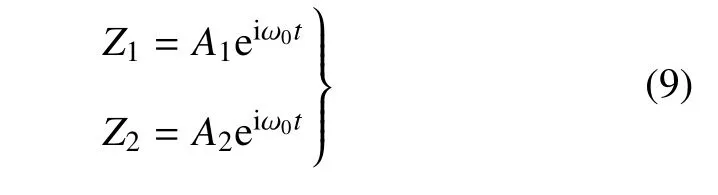
将式(9)代入式(8),解得

式中
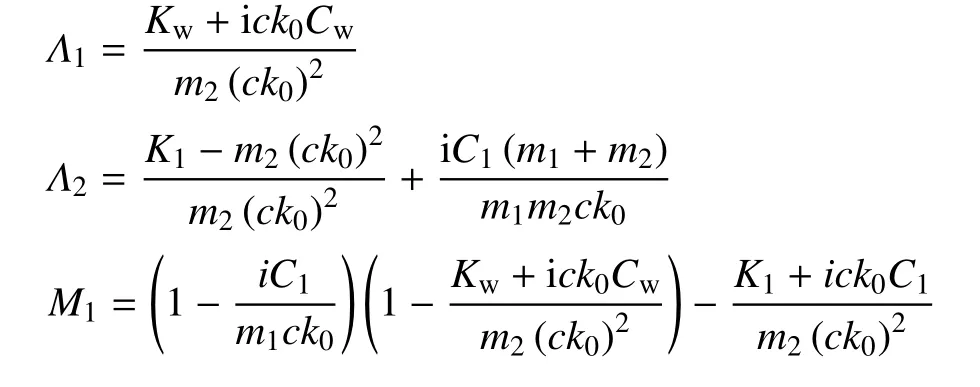
将式(10)依次回代到式(9)、式(7)、式(2)中,即可确定出轮胎的动态压缩量

将式(12)分别代入式(3)~式(5),则确定出qd(t),fd(t),a(t).

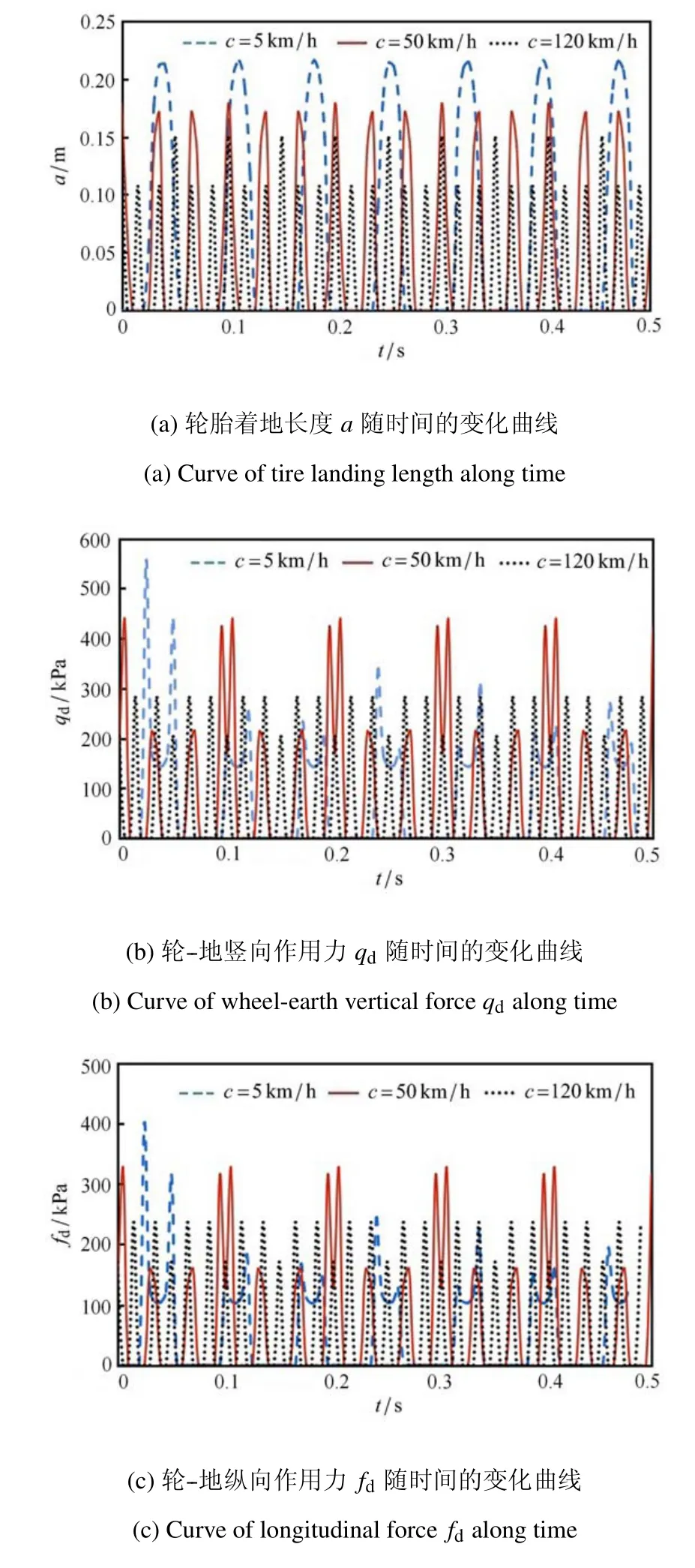
图2 a,qd,fd 随时间的变化曲线Fig.2 Curves of parameters a,qd,fd along time

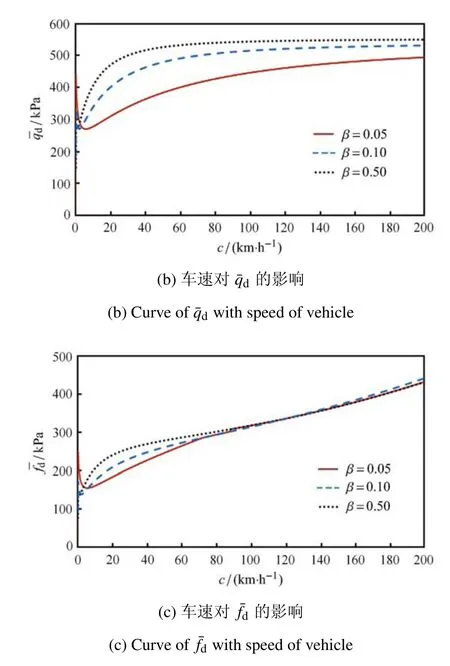
图3 物理量幅值,?, 随车速的变化曲线Fig.3 Curves of,?,with speed of vehicle
实验研究发现,轮胎充气压力增大,轮胎刚度增大而阻尼减小.为综合反映轮胎包容性的影响,利用实验拟合公式将轮胎刚度系数Kw和阻尼系数Cw统一用轮胎充气压力表示[32-33]
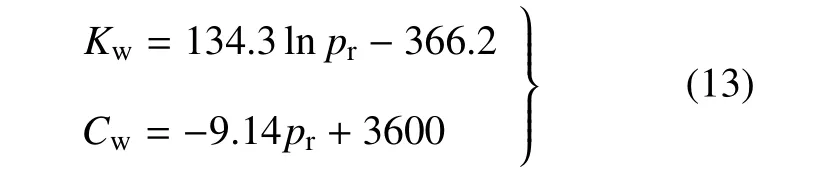
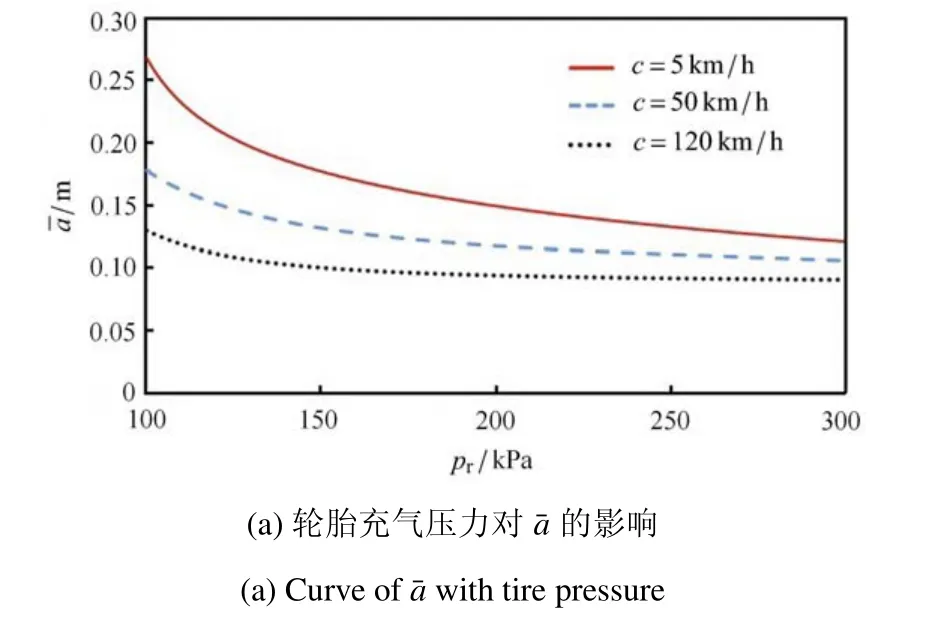
图4 轮胎充气压力对,,的影响Fig.4 Curves of,, with tire pressure

图4 轮胎充气压力对,, 的影响(续)Fig.4 Curves of ,, with tire pressure(continued)
式中,pr为轮胎充气压力(kPa).图4 为三物理量幅值,,与轮胎充气压力的关系曲线.图中发现,汽车在中、低速行驶时,胎压对,,影响显著;随着pr增大,轮胎着地长度减小,轮--地作用力,增大.而高速行驶时,胎压对三物理量幅值几乎无影响.
2.2 地基动力方程及求解
均质弹性半空间直角坐标系下的运动方程为

本构方程
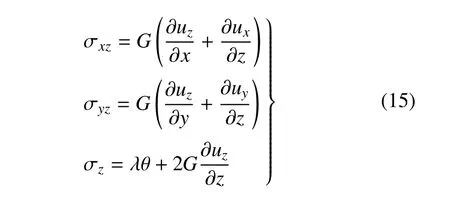
式中,σxz,σyz,σz为地基中一点的应力分量;对时间坐标引入如下Laplace 变换

式中,“ˆ”表示对应物理量的Laplace 变换,s为变换参数.对式(2)进行Laplace 变换后,写为

对x,y坐标引入如下双重Fourier 变换对
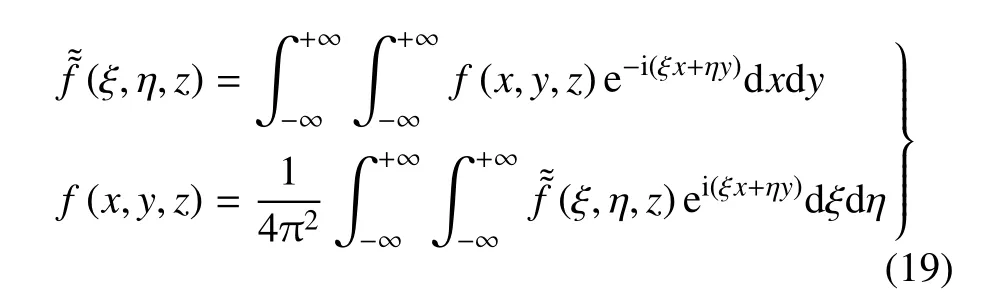
式中,ξ,η 为Fourier 变换参数,“≈”表示对应物理量的双重Fourier 变换.对式(18)进行双重Fourier 变换,将其化为关于(ξ,η,z,s)的二阶常微分方程
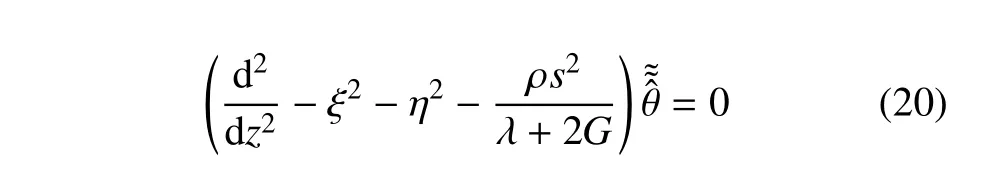
求解式(20),得到

对式17(a)~式17(c)也进行双重Fourier 变换,
并将式(21)代入,整理后得到
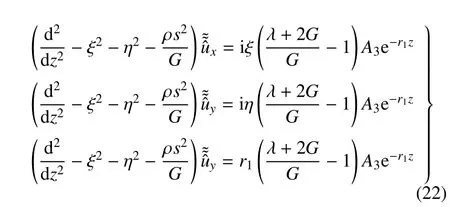
求解常微分方程组(22),得到变换域中地基的位移解

对本构方程(15)做Laplace 和Fourier 变换后,并将式(21)、式(23)代入,得出变换域中地基的应力解

半空间表面(z=0)处的边界条件写为
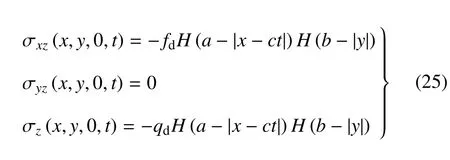
式中,H()表示Heaviside 阶跃函数.对式(25)进行双重Fourier 变换和Laplace 变换后得到
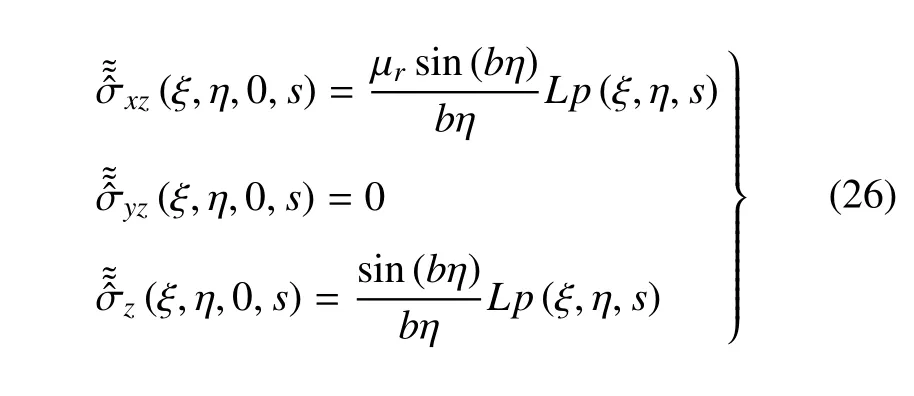
式中
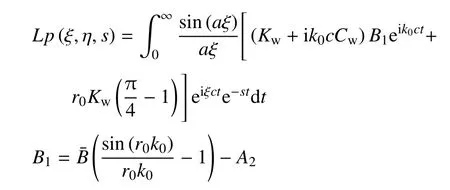
将式(23)、式(24)代入式(26),得到

将式(28)回代到式(23),则得到地基位移在变换域的解析式

通过对式(29)做双重Fourier 逆变换和Laplace逆变换,并取z=0,则可得到空间域中地表位移(x,y,0,t),(x,y,0,t),(x,y,0,t).
3 算法验证
根据前文推导出的公式,编写程序计算地表振动位移,其中Fourier 逆变换采用离散傅里叶逆变换(IDFT)实现,Laplace 逆变换采用Crump 法[34]做数值反演.为了进行对比,地基参数取值与文献[35]相同,杨氏模量E=2.69 × 108Pa,密度ρ=1550 kg/m3,泊松比ν=0.257,P波波速=263 m/s.通过观察式(3)、式(5)、式(12)能够发现,若取地面不平度幅值˜B=0,则qd,a都变为定值,再取轮胎滚动阻力系数μr=0,则fd=0,本文模型即可退化为弹性半空间表面作用移动矩形载荷的地基动力响应问题,退化模型与文献[35]相同.图5 为观测点A(350,0,0)处的竖向位移,图中显示本文结果与文献解能够很好的吻合.图5 还反映出,当同时考虑竖向和纵向作用力时,地表振动位移明显增大.

图5 计算结果对比Fig.5 Comparison of calculation results
4 数值结果和讨论
将2.1 节的汽车模型代入地基模型,即可算出汽车行驶诱发的地基振动位移.图6 为计算出的t=0.1 s 时刻,地表竖向位移uz的空间分布,对比图3(a)与图3(b)的位移坐标值可以发现,车速增大时地表位移明显增大.并且从图3(a)中发现,振动位移沿纵向(x方向,汽车行驶方向)和横向(y方向)的分布存在差异.为进一步考察该问题,图7 绘出了振动位移分别沿x,y方向的衰减曲线.图中显示,在近场区域,沿纵向分布的振动位移明显大于横向,位移衰减距离也略大于横向.通过对比图8(a)~图8(c) 还能发现,汽车行驶速度越低,则振动位移沿纵、横向分布的差异越大.需补充的是,图7 和图8 给出的位移分布曲线与文献[30]的实测曲线分布规律一致,进一步验证了本文模型的可靠.

图6 地表竖向位移uz 空间分布Fig.6 Distribution of vertical displacement
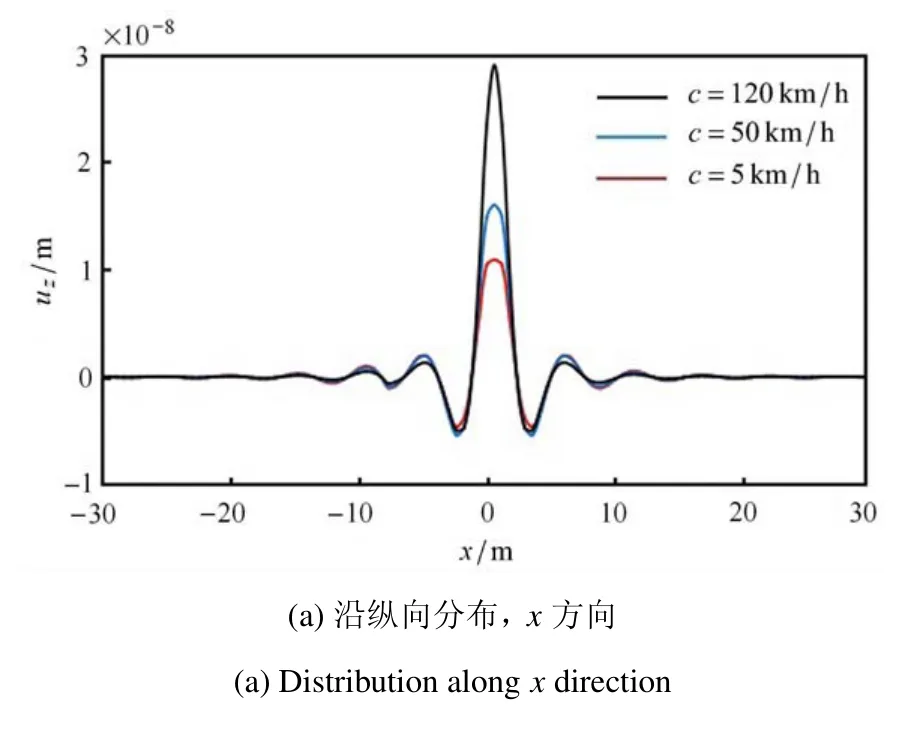
图7 竖向位移沿纵、横向的分布Fig.7 Distribution of vertical displacement along longitudinal and lateral directions

图7 竖向位移沿纵、横向的分布(续)Fig.7 Distribution of vertical displacement along longitudinal and lateral directions(continued)
图9 为不同地面不平度因子β 取值下,地表振动位移的横向分布图,由图可知,地面不平度对地表振动影响非常大,地面越不平顺,振动位移越大,纵向分布具有相同性质.图10 反映了轮胎充气压力pr对地表振动位移的影响,对比图10(a)和图10(b)发现,汽车在高速行驶时,pr对地表振动几乎无影响;而在较低车速时产生一定影响,pr越大,地表振动位移越大.

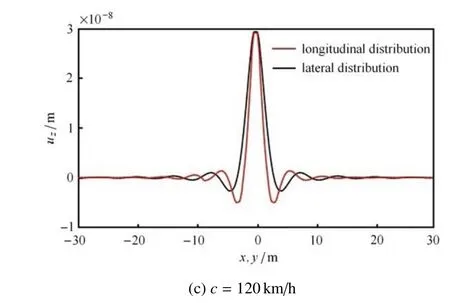
图8 不同行驶速度下振动位移纵、横向分布对比Fig.8 Distribution comparison between longitudinal and lateral directions at different velocities
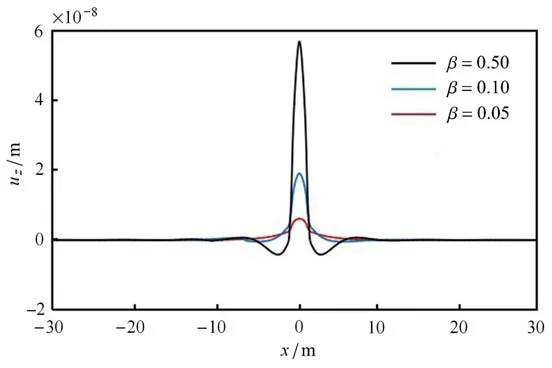
图9 地面不平度对振动位移的影响Fig.9 Influence of ground irregularity β on vibration displacement
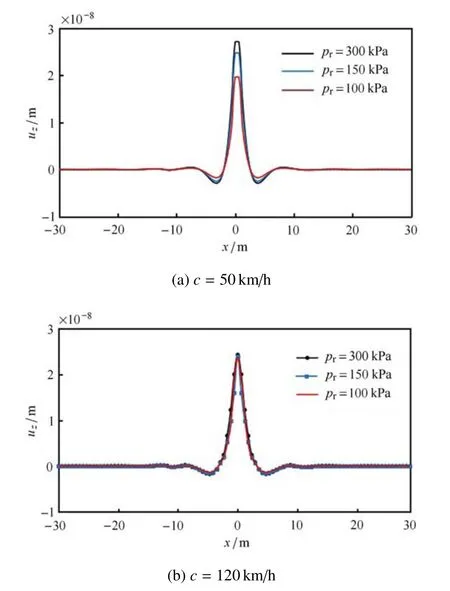
图10 轮胎充气压力对地表振动的影响Fig.10 Effects of tire pressure on surface vibration
5 结论
利用1/4 车体模型和弹性滚子接触模型建立车--地耦合系统的振动分析模型.模型中所有参数都物理意义明确,均可通过查表或试验确定(地基参数).因此,本文给出的模型和算法可以作为一种预测汽车行驶诱发地基振动的理论方法.
文中通过理论推导和数值计算,分别讨论了汽车行驶速度、地面不平度及轮胎充气压力对车--地相互作用和地表振动的影响规律.可总结出以下几点结论:
(1) 相对而言,车速对于轮--地作用力的峰值影响有限(尤其高速行驶时),而对载荷激励频率影响较大.故,车速主要通过改变车--地相互作用的激励频率来影响地表振动.
(2)地面不平度对车--地相互作用力和地表振动的影响最为显著.
(3)轮胎包容性在较低车速时对车--地相互作用力和地表振动有一定影响,随着车速增大,影响逐渐消失.

