基于内聚力模型的高速水流聚脲基涂层剥离破坏模型研究
李炳奇 张振宇 李 斌 刘小楠 杨旭辉
*(中国水利水电科学研究院流域水循环模拟和调控国家重点实验室,北京 100083)
†(河北丰宁抽水蓄能有限公司,河北承德 068350)
**(南水北调中线干线工程建设管理局河南分局,郑州 450000)
引言
水工建筑物的冲磨和空蚀破坏是水利水电设施最为常见的病害之一,特别是在水流量和水流速均较大的工程中,这种破坏更为严重.通常水利水电设施采用一些防护措施提高水工建筑物的抗冲耐磨性能[1-2].如采用具有抗冲耐磨性能的混凝土[3]、钢渣高性能混凝土[4]和钢板衬护[5].这些抗冲耐磨技术只能在一定程度上满足普通条件下水工建筑物的抗冲磨要求.但对于一些温度和湿度变化较大条件,通常采用聚脲弹性技术作为泄水建筑的防护材料.聚脲弹性体材料在普通环境下具有抗磨蚀、耐老化、抗腐蚀、抗冲击及独特的施工性能,在泄洪建筑物防护体上得到广泛应用[6-7].但在泄水水流速度较高的高水头水电工程中,聚脲涂层的剥离破坏和泄水建筑物的磨损破坏问题仍较严重.
许多学者采用试验和数值分析方法对不同堤坝特性[8-9]、防护材料[10-12]和厚度的防护层、冲刷特性[13-14]在高速水流冲刷作用下的冲刷破损和侵蚀机理进行了研究.上述研究中对高速水流作用力分析时,主要考虑高速水流的冲刷和磨损作用.但是泄洪建筑物在高速水流作用下不仅仅包含高速水流的冲刷和磨损,由于泄洪时水流呈现复杂的湍流模式,水流对建筑表面还会产生脉动压强和空蚀作用,这些载荷对泄洪建筑物表面冲刷破损有重要影响.并且聚脲涂层一般均能满足抗冲耐磨要求,破坏形式表现为聚脲涂层与混凝土基底的剥离破坏.
由于聚脲涂层材料为超弹性材料,聚脲基涂层与泄洪建筑物间的剥离破坏问题是非常复杂的高度非线性、非连续问题,传统的理论模型很难准确描述界面由裂缝萌发直至破坏的过程,目前对高速水流作用下聚脲基涂层与泄洪建筑物之间的剥离破坏研究尚无.对于此类问题,通常采用内聚力模型[15-16].很多学者采用其来描述不同界面的剥离破坏,如采用内聚力模型对均质材料[17]、复合材料[18]、接触界面[19-23]、钛合金支架与聚脲涂层[24].
为了探究高速水流作用下泄洪建筑物与聚脲基涂层之间的剥离破坏机理,本文建立了泄洪高速水流对泄洪建筑物的剥离破坏模型.模型中采用内聚力模型来描述聚脲基涂层与泄洪建筑间的剥离破坏;高速水流对泄洪建筑物的力学作用模型考虑了水流作用对泄洪建筑物的拖曳力、冲击力、脉动压强和托举力作用.并采用剥离破坏试验验证了模型的可行性,为泄洪建筑物的抗冲耐磨设计提供理论依据.
1 高速水流剥离破坏模型
高速水流作用下聚脲涂层一旦产生剥离破坏,水流作用力则全部作用在泄洪建筑物上,使其产生严重的侵蚀破坏.对此进行修复不仅影响水电站的正常运行,而且花费巨大.为了使得水电站能够健康、持续的运行,根据聚脲基涂层与混凝土之间的剥离破坏过程,基于内聚力模型理论,建立了高速水流作用剥离破坏模型.
1.1 高速水流作用力
泄洪洞泄洪时,泄洪建筑的聚脲基层承受高速水流的冲刷作用,由于水流流动过程为复杂的湍流,作用在聚脲基层上的载荷非常复杂,目前还未有合理的模型能够准确描述这样的水流运动形态.因此,在分析水流对聚脲基层的作用时,假设水流作用在聚脲基层上的载荷主要有拖曳力、冲击力、脉冲力、托举力,各载荷计算方法分别如下.
1.1.1 拖曳力
高速水流作用下,聚脲基涂层所受到的水流作用力一般分解为水平拖曳力和垂直上举力.受力体受到的拖曳力与其自身的形状相关,在本研究中,由于聚脲基涂层为平通的平面形式,因而采用如下的经典的拖曳力计算公式
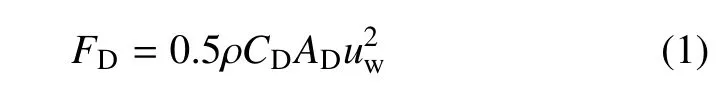
其中,FD为拖曳力,AD为参考面,即水流投影面积,uw为无扰动流的水流流速,ρ 为水密度.CD为拖曳系数,对于水流对聚脲基涂层的拖曳系数,根据文献[25]对其进行取值,CD=0.09.
1.1.2 高速水流冲击力
高速水流以一定流速作用在聚脲涂层,对其产生一定的冲击作用,冲击载荷可根据牛顿动能定理进行计算

其中,F为高速水流对聚脲基涂层的冲击力,u2为水利初始速度,u1为水利冲击后的速度.
1.1.3 高速水流脉动压力
紊流的脉动流速遇到边界或其他障碍时,动能转变为压能,水流产生脉动压力.如果认为湍流为均质各向同性,脉动压力公式可表示为
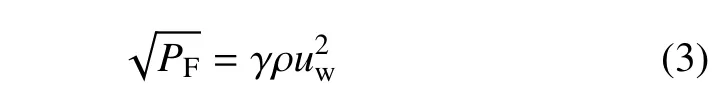
1.1.4 托举力
高速水流在泄洪建筑物混凝土表面产生垂直于潜在的流动方向的力称作为托举力.与拖曳力对比,托举力是平行于水流方向的力,上浮力通常作用于一个向上的方向以抵消重力,但它可以作用与流动方向成直角的任何方向.水流对建筑物表面的上浮力可表示为[28]

式中,Ff为托举力,S为水流在建筑物表面的投影面积,Cf为上浮力系数,其由水流的方向、马赫数和雷偌数决定,计算时取值Cf=0.08[29].
1.2 剥离破坏模型
泄洪建筑物泄洪时,泄洪建筑物聚脲基涂层遭受水流冲击和拖曳等载荷作用,当水流作用超过聚脲基涂层与混凝土之间的粘接强度时,涂层与混凝土界面之间开始产生裂缝,并且在水流载荷作用下不断扩展,直至产生完全破坏.采用内聚力模型描述界面的剥离破坏,建立了高速水流作用剥离破坏模型来描述此过程,模型如图1 所示.

图1 界面剥离破坏模型示意图Fig.1 Schematic of debonding failure model in interface
根据内聚力模型思想[15-16],模型中剥离破坏区域可以分为两部分,一部分为聚脲基涂层与泄洪建筑物完全分离;另一部分为聚脲基涂层与泄洪建筑物未完全分离,并且二者之间还存在黏聚作用,如图2 所示.
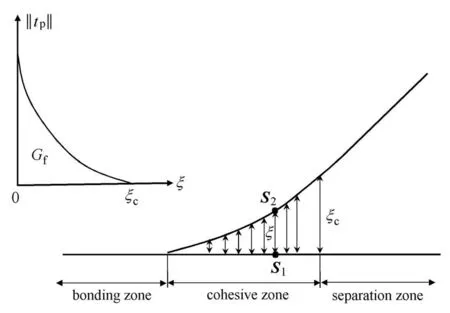
图2 内聚力模型示意图Fig.2 Schematic of the cohesive zone model
采用内聚力模型来描述黏聚裂缝区的力学性能,聚脲基涂层与泄洪建筑物间由开始产生裂缝,一直到完全分离,内聚区中的应力--位移关系可由下式表达

其中,ft为界面表面力,Gf为界面的断裂能,tp为界面的拉应力,ξ 为内聚力单元界面间的相对位移,可由下式表示

其中,s1为变形前位置坐标,s2为变形后位置坐标.
黏聚裂缝区内聚力模型的牵引力表达式如下

Kc为内聚区界面应力与相对位移关系中的刚性系数,K为界面材料的弹性模量,当相对位移ξ ≪0时,此时Kc=K.
采用界面材料的强度特性来判断界面是否产生裂缝,界面牵引力与相对位移之间的关系式表达如下

当表面力tp在向量法向(n)方向的分量应力超过材料的抗拉强度(ts)时,即发生破坏,表达式如下
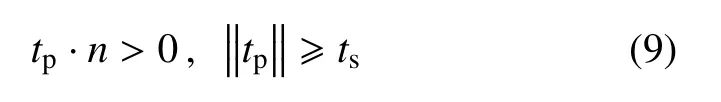
1.3 模型在有限元中形式
通过在有限元模型中添加无厚度的内聚力单元,表征聚脲基涂层与泄洪建筑物防护体界面的剥离破坏过程,采用标准的应力单元描述基体材料的力学行为.模型的有限元形式方程、本构关系以及计算时的损伤起始原则、演化原则和接触碰撞介绍如下.
(1)有限元方程
剥离缝处考虑流固耦合、内聚力单元,根据虚功原理有限元方程[30-33]如下
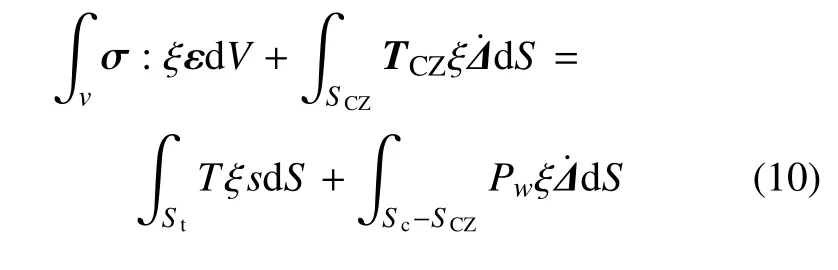
其中,St表示力学边界;SCZ表示内聚力要素边界;SC表示裂缝边界.其中σ 和ε 分别为体元素的应力和应变矢量,Tcz为内聚力单元牵引力矢量,Δ 为内聚区界面的相对位移矢量,T为外部载荷矢量;Pw为劈裂水压力,如图3 所示.
根据流固耦合理论,水压P计算如下
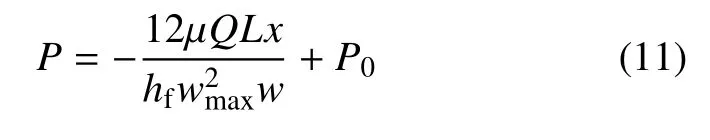
式中,Q为任意时刻剥离缝处水流流量,剥离缝最宽处宽度为Wmax,水压力为P0,剥离缝高度为hf,w为以剥离缝最宽处的中心为原点,沿剥离缝扩展方向建立X轴,则与原点距离为x处的剥离缝宽度;L为剥离缝长度,μ 是水的黏度.
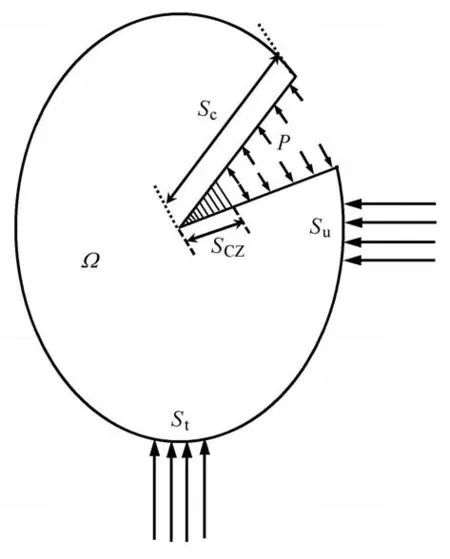
图3 裂缝边界条件示意图Fig.3 Schematic of crack boundary conditions
计算时采用Newton-Raphson 迭代法进行迭代计算,内聚力所做虚功可用下式表示

其中,Tn和Tt分别为法向和切向牵引力,ξΔn和ξΔt分别为法向和切向张开位移,A为外载荷作用的外表面的面积,J为内聚力表面变形前后的转换矩阵.将内聚力单元形函数代入上式,当前形态的离散虚功ξWc可表示如下

其中,N为内聚力单元形函数.虚功的第一变量dξWc可由下式表示
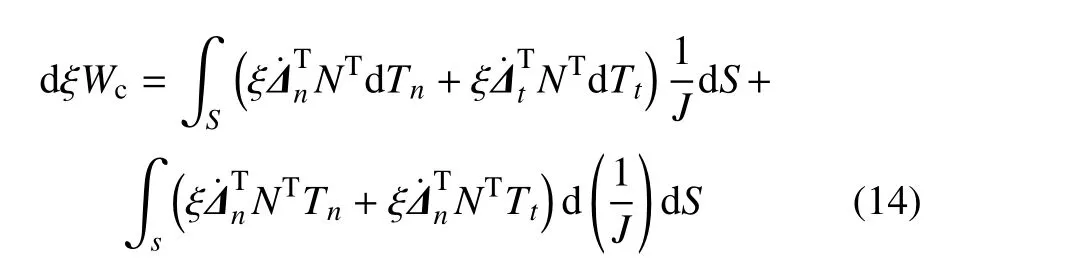
上式中第二项考虑了内聚力单元的延伸.对于内聚力单元延伸量较小时,式(14)可以简化为
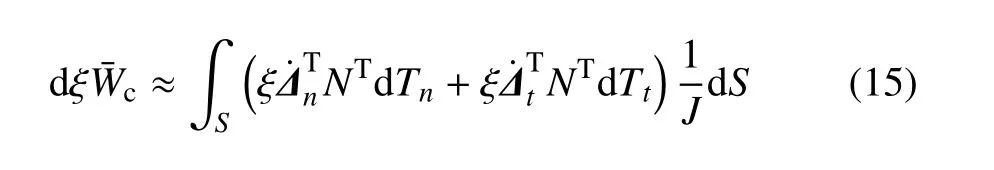
牵引力增量与位移关系如下

将式(16)代入式(15),可得内聚力单元刚度矩阵形式,如下
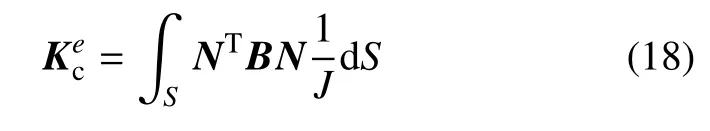
因此,总的单元刚度矩阵如下式
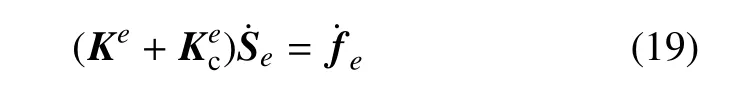
式中,Ke为基体单元刚度矩阵,为单元位移矩阵,为外载荷矩阵.
(2)本构关系
内聚力单元的本构关系通过牵引--分离法则(TSL)表征,其失效机制可分为损伤起始、损伤演化和断裂失效3 个阶段,即当内聚力单元的应力或应变状态满足损伤起始准则后,内聚力单元进入损伤演化阶段,达到相应的断裂失效条件后,内聚力单元进而完全破坏并被移除.
牵引--分离法则[34]中内聚单元的本构关系如下

其中,t为内聚单元牵引应力矢量,由法向应力分量t1和切向应力分量t2;ξ 为内聚单元张开位移矢量,由法向张开位移分量ξ1和切向张开位移分量ξ2,K为内聚单元刚度矩阵,其由法向刚度分量K11和切向刚度分量K22及剪切刚度分量K12组成.
(3)损伤起始准则
当内聚单元的应力或应变满足某种损伤初始准则时,衰减过程即开始发生.计算中通常采用二次名义应力准则[31],准则中当两个方向应力率的二次方相加达到1 时,损伤演化开始,公式表示为
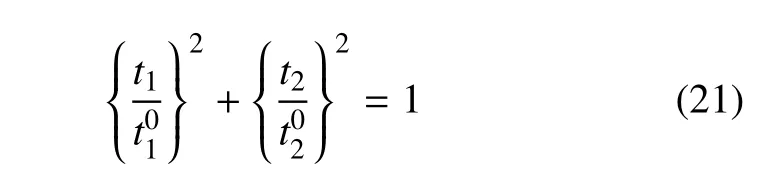
式中,t1,t2分别表示内聚单元法向应力和两个切向应力,,表示内聚单元法向和切向能承受的最大应力.由于内聚单元在纯受压状态下不可能遭受损伤破坏.
(4)损伤演化准则
为了描述内聚力单元的损伤演化,引入了等效位移δm,其计算公式如式(23).在损伤出现后,继续对其进行加载,通过损伤变量D描述内聚力单元的损伤程度,其计算公式如式(24).损伤变量D初始值为零,即内聚力单元未出现损伤;D从0 单调增加至1,即内聚力单元进入损伤演化阶段;当D=1 时,内聚力单元完全破坏,即界面完全断裂.内聚单元各应力分量与损伤变量关系式(25)和式(26).

采用B-K 断裂准则[35]进行判断,内聚力单元达到断裂准则后,则将被移除.
(5)接触碰撞
聚脲基涂层与混凝土之间剥离破坏后,此时内聚力单元将被移除,分离区的聚脲基涂层自身以及和混凝土之间在水流作用下均会产生相互接触作用.此时采用通用接触算法来分析接触面的法向作用和接触面的切向作用两个部分,其中切向作用又包括接触面间的相对运动和接触面间可能存在的摩擦剪应力.
通常接触面法向行为定义为只有在两物体未产生分离时才会传递法向的压力P,一旦两个接触面间产生间隙就不会存在法向压力,此种法向接触行为称之为硬接触[32],即接触面上任意点的接触压力P是其咬合过度(h)的函数,即P=P(h),其中

这种法向行为在接触碰撞计算时物体表面就不可能会发生穿透现象.
接触面切向的接触作用遵循库伦法则,当接触面等效接触应力小于临界应力,接触面之间无相对滑动时,即处于压紧粘结状态;当接触面等效接触应力大于临界接触应力时,接触面之间产生相对滑动.其中等效接触应力和临界接触应力可分别由下式计算.

2 模型验证
2.1 聚脲涂层与混凝土剥离破坏试验
为研究聚脲基层与泄洪建筑物防护体界面在高速水流作用下的剥离破坏,采用剥离试验研究其界面的剥离特性,并探讨了界面在不同剥落角度作用下的玻剥离破坏.
(1)试验条件
试验中采用剥离试验系统对界面剥离试验进行加载,试验系统中包括加载设备、数据采集设备和试件固定设备,试验试件和试验条件分别如图4 和图5 所示.试验试件主要有聚脲基涂层与混凝土,二者通过底漆粘接在一起,尺寸为60 mm×20 mm×2 mm.试验时将粘贴好的试件固定到试验架上进行加载,直至界面产生剥离破坏,数据采集设备记录试验过程中的载荷--时间、位移--时间等数据.

图4 试验试件Fig.4 Test specimen

图5 剥离破坏试验系统示意图Fig.5 Schematic of the debonding failure tests system
此外,通过调整剥离界面角度,即界面与水平面之间的夹角,探讨不同剥离界面角度条件下界面的剥离破坏.试验中共包括了6 个剥离界面角度,即15°,30°,45°,60°,75°,90°,由于聚脲基层与混凝土界面采用底漆粘接,界面粘接强度存在离散,因而每组试验做3 组平行试验.
(2)试验结果分析
三组试验界面拉应力与张开位移关系曲线如图6所示,由图6 可发现,3 组试验结果拉应力与张开位移关系曲线形式基本相同,均可分3 个阶段;首先是界面在拉应力的作用下,界面黏聚层开始产生位移,并且其随拉应力呈线性变化;随后,随着界面载荷的增大,粘结层变形达到一定程度,产生了不可恢复的变形,界面出现塑性变形,在此阶段界面载荷达到最大值;第3 阶段为界面完全张开,当拉应力在垂直界面方向的分量超过粘结层的抗拉强度时,聚脲基涂层与混凝土产生完全分离,在拉应力与张开位移曲线中表现为拉应力值的突降.

图6 界面拉应力与张开位移关系曲线Fig.6 The curve between the tensile stress and opening displacement

图6 界面拉应力与张开位移关系曲线(续)Fig.6 The curve between the tensile stress and opening displacement(continued)
不同剥离倾角条件下,界面拉应力达到最大值时的张开位移基本相同,即界面产生完全破坏的张开位移,均约为0.11 mm.由于当剥离倾角较小时,拉力在垂直界面方向上分离也较小,需要更大的载荷使得界面产生剥离破坏.当剥离倾角在75°~90°时,界面剥离破坏时的拉力相差很小,基本相同;当剥离倾角在15°~75°时,界面剥离破坏时的拉力随着剥离倾角的增大而减小.
2.2 模型验证
高速水流作用下,拖曳力和冲击力作用方向为平行于聚脲基涂层,脉动压力和托举力作用方向为垂直于聚脲基涂层,其合力方向为斜向上.如此可知,高速水流作用下聚脲基涂层的受力特性与剥离试验中的聚脲基涂层受力特性相同.因此,采用上述剥离模型对试验进行计算,验证模型的可行性.
根据试验建立仿真模型,模型共包含混凝土板、聚脲基涂层两部分(如图7 所示).模型中采用实体单元描述聚脲基涂层和混凝土的力学行为,采用内聚力模型描述界面的剥离破坏特性.计算时在混凝土底板上施加竖向和水平位移约束.根据1.1节中高水流作用下各载荷计算公式对其分别进行计算,为了使界面能够产生剥离破坏,水流流速应尽量选取大些,选取为30 m/s.计算得出拖曳力、冲击力、脉动压力和托举力分别为40.5 kN,30 kN,23.23 kPa,36 kN,剥离倾角为40°.计算中冲击力垂直于聚脲涂层端部,拖曳力平行于聚脲涂层,脉动压力和托举力垂直于聚脲方向,有限元模型中载荷施加示意图如图7 所示.
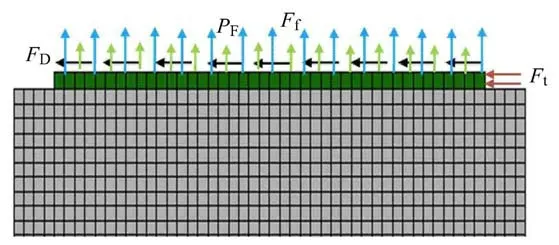
图7 试验有限元模型Fig.7 Numerical model of tests
混凝土材料应力--应变关系采用弹性变形模型进行描述,混凝土弹性模量和泊松比分别为32.5 GPa 和0.2;聚脲基涂层也采用弹性模型进行描述,弹性模量和泊松比分别为49.5 MPa 和0.37.
由试验曲线可知,当剥离倾角为90°时,界面破坏时的载荷基本为粘结层拉伸破坏所需的载荷,约为50 N,计算界面材料抗拉强度

式中,F为界面破坏时的拉力,A为受力去面积,聚脲基涂层长度为2 cm,宽度取单位宽度1 mm,则τ=2.5 MPa.
根据广义断裂能的定义,其值可根据拉应力与张开位移曲线所围成面积计算得出,通过试验中的曲线可计算其值约为125 J/m2.法向和切向刚度根据文献[36]进行选取,取值分别为1.0×1013Pa/m 和1.0×1012Pa/m.计算时选择二次应力判断准则作为裂纹萌生准则,裂纹扩展准则选择B-K准则.
选取试验有限元模型中端部顶点为载荷--位移变化监测点,加载过程中其拉应力与张开位移的变化关系如图8.试验和数值计算结果基本吻合,验证了上述模型在描述高速水流作用下界面剥离破坏的可行性.
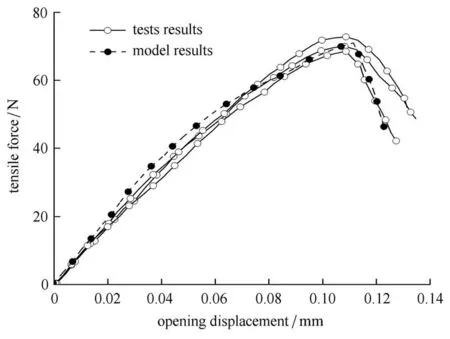
图8 试验与数值计算结果对比Fig.8 Comparison of test and numerical results
3 结论
本文研究了高速水流作用下泄洪建筑物与聚脲基涂层之间的剥离破坏机理,建立了泄洪高速水流对泄洪建筑物的剥离破坏模型,并采用剥离破坏试验验证了模型的可行性.根据上述研究,主要得出以下结论:
(1)基于高速水流的流态形式,水流作用对泄洪建筑物的载荷主要包括拖曳力、冲击力、脉动力和上浮力,确定了高速水流对泄洪建筑物的力学作用模型;
(2)采用内聚力模型表征聚脲基涂层与泄洪建筑物防护体界面的剥离破坏过程,给出了模型的有限元形式方程、本构关系以及损伤起始原则、演化原则和接触碰撞,建立了泄洪高速水流对泄洪建筑物的剥离破坏模型;
(3)通过聚脲涂层与混凝土基底的剥离破坏试验得到了剥离破坏过程中应力--位移变化关系,得到了不同剥离倾角下界面剥离破坏的拉应力与倾角之间的变化规律;
(4)根据剥离破坏试验得到的界面剥离破坏断裂模型参数,并对模型进行了验证.试验结果与模型计算结果吻合良好,为泄洪建筑物的抗冲耐磨设计提供理论依据.

