无位置传感器的永磁同步电机控制技术综述

阎宝君，刘 健，梁禹升，王世奇

（武汉工程大学 电气信息学院，武汉430205）

近些年来，随着新型电力电子器件的应用和电力电子技术的发展，永磁同步电机不断改进，其优点在交流调速系统应用中表现得越来越明显。 永磁同步电机具有相对更高效率、高功率因数、高功率密度，更低的温升、低电枢反应，此外其调速和力矩性能指标也更好。 在其性能优越的同时，运行控制算法也更为复杂。 传统的有位置传感器永磁同步电机，一般采用编码器等机械式或者霍尔元件等电磁式位置传感器，这些传感器增加了电机本体的体积，而且容易受到外界环境因素干扰和影响，使系统可靠性降低。

针对各种应用场合，对于不同阶段额定运行速度的永磁同步电机和同一应用中的不同运行阶段，其适合采用的控制方法有所不同。 故在此对静止、起动和低速运行、中高速运行和全速度范围下的永磁同步电机较为常用并且成熟的转子位置检测及控制的方法做了列举和分析。

1 转子初始位置检测

永磁同步电机起动一般需要获取其在静止状态下的转子位置信息，这对于有位置传感器的系统实现较为容易，而对于无位置传感器控制技术，永磁同步电机转子初始位置检测无法单纯依靠电机电气特性。 目前业界较为成熟的检测方式普遍利用电机本体的结构凸极性和非线性饱和性。

1.1 电感参数法

内嵌和内埋式永磁同步电机直轴电感和交轴电感大小存在差异，电感参数法通过向绕组分2 次通入线性无关的电压矢量，通过测量瞬时响应电流可以计算出电感参数矩阵，由此得出转子位置信息[1]。 其原理具体如下：

令

电感参数矩阵为

分2 次分别向定子绕组通入足够短暂的测试电压uα1，uβ1，uα2，uβ2，测得的瞬时响应电流分别为iα1，iβ1，iα2，iβ2，列写参数方程为

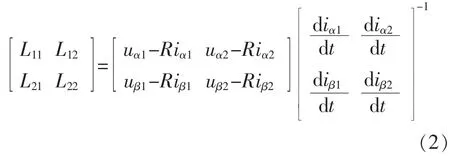
进一步可解得转子位置的电角度为

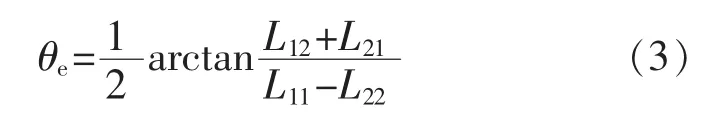
文献[1]使用电感参数法对电机初始位置检测进行了试验，最大转子位置角误差为±10°，证实此方案可行。

1.2 信号注入法

信号注入法，主要是指在永磁同步电机在初始静止状态下，通过向电机定子通入测试电压信号，在其系统检测的响应电流中可以分离出转子位置信息。 由所施加的电压信号方式和类型不同，可以分为高频脉振电压注入法、旋转高频电压注入法、低频电压信号注入法、脉冲信号注入法等。

静止高频脉振电压注入法在旋转坐标系下实施，在其d 轴或q 轴注入高频的脉振电压信号，然后采用锁相环等算法从其响应电流中获取转子位置角。文献[2]中向q 轴通入高频测试电压，如图1所示。 而文献[3-4]中向d 轴通入高频测试电压，如图2所示。 研究发现，q 轴注入会引入额外的脉动，相对于d 轴注入来说静态性能较差，实际应用中采用不多。

图1 d 轴或q 轴脉振高频电压注入法Fig.1 d-axis or q-axis pulse high frequency voltage injection method

旋转高频电压注入法在静止的αβ 坐标系中注入随电角度旋转的高频电压信号，如图2所示。由于转子位置角信息包含在负序电流中，可以直接提取。 该方法通用性较好，可配合适用于多种控制算法框架，难点在于对电流采集精度要求较高，需要性能较高的滤波器配合使用。

图2 旋转高频电压注入法Fig.2 Rotating high frequency voltage injection method

低频电压信号注入法不依赖电机参数及其凸极性性质。 其原理是，向电机绕组中注入低频的电压信号，电机转子在低频电压信号激励下会产生微振，并且引起电机反电动势波动。 这些波动包含了转子位置信息，且波动会直接反应在响应电流中。 该方法根据注入电压信号与注入位置的不同，也可以分为旋转低频注入法和脉振低频注入法。

脉冲注入法向电机绕组通入特定脉冲电压矢量信号，也可以从响应电流中获取转子位置角信息。 文献[5]和文献[6]中提供了PWM 谐波脉冲注入方法，而文献[7]中使用矢量测试电压脉冲注入法。PWM 谐波脉冲注入法采用常规的PWM 调制方式，控制方式易于实现，但是硬件需要具有较高的采样精度和采样速度，并且更适用于电感较小的永磁同步电机系统中。 矢量测试电压脉冲注入法一般需要构造特殊的电压矢量，控制相对复杂，并且电流畸变较大，需要采用特殊算法进行处理，文献[8]中的试验通过注入等宽电压脉冲矢量，如图3所示。 检测电流响应来获取初始位置，精度为±1.875°电角度。

图3 脉冲注入法电压矢量施加次序Fig.3 Voltage vector application sequence of pulse injection method

2 起动与低速运行控制

2.1 三段式起动法

所谓三段式起动方法（如图4所示），指采用转子预定位、强制起动、闭环运行3 个步骤的无位置传感器控制。

预定位阶段是指在电机静止时不采用信号注入方式确定转子位置，而是通过向绕组通入固定电压脉冲序列，将电机转子转动固定在固定的位置上；电机转子初始位置已知，电机可以从已知的初始位置处强制起动，强制起动即向绕组施加规定方向依次旋转的电压矢量，将转子从静止状态带入低速运行状态，当电机转速升至额定转速的15%左右，无传感器位置估计算法可以获得可靠、稳定的输出，从而转入闭环运行阶段。

图4 三段式起动法示意图Fig.4 Schematic diagram of three stage starting method

三段式起动方法为一种开环起动方法，实现简单，但因为在预定位阶段转子转动可能导致电机系统存在反转情况，所以只适合用在起动转矩较小且允许起动反转的系统中[9]。

2.2 I/f 控制法

I/f 控制[10]即恒流频比控制，是变频调速的一种，其特点为在电机起动和运行过程中保持电流闭环，而转速开环。 电流的闭环可以保持电磁转矩的跟踪和调节能力，适用于对转矩要求较高且起动时间较长的永磁同步电机控制系统。

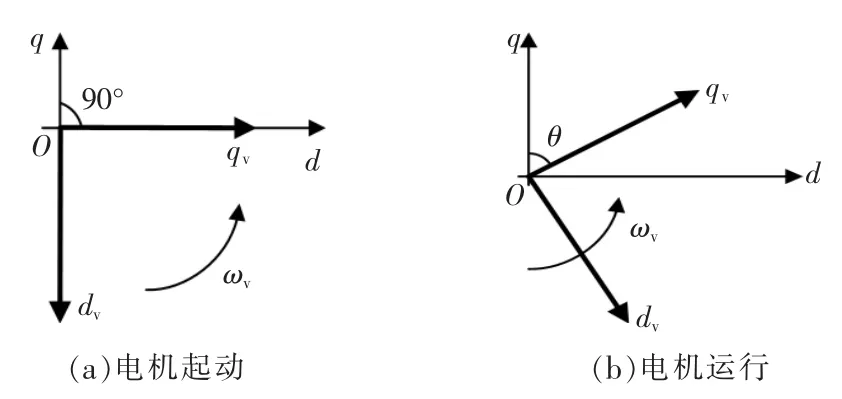
图5 I/f 控制电机起动及运行原理Fig.5 Motor starting and operation principle of I/f control

永磁同步电机I/f 控制起动时，实际同步坐标系领先虚拟坐标系90°电角度，如图5a 所示。 运行过程中，电机转子跟随虚拟同步坐标系旋转，如图5b 所示，其输出转矩为

起动过程中运动方程为

2.3 V/f 控制法

V/f 控制即恒压频比控制，通过同时控制电机电压和频率，使磁通稳定不变。 V/f 控制不需要获取电机转子位置，是一种完全开环的控制方法，不能直接控制电机转矩电流，也不能准确控制转速，容易出现振荡且调速范围较小[11]。 但是，V/f 控制实现简单，对硬件系统要求不高，控制参数也不需要特别精确，适用于精度不高的低成本风机类负载系统中。

3 中速与高速运行控制

永磁同步电机运行在中速或高速阶段，其反电动势是可靠稳定的，此时注入信号会使额外损耗增大且容易破坏系统稳定性。 所以，在该范围内无位置传感器控制一般不采用基于电机凸极模型性质的方法，而更多采用具有更好效果的基于基波模型性质的方法。 这类方法包括模型参考自适应法、观测器法、扩展卡尔曼滤波法等。

3.1 模型参考自适应法

永磁同步电机的模型参考自适应法，主要由参考模型、可调模型和自适应算法构成[12]，如图6所示。 实际系统设计中，一般将永磁同步电机本体作为参考模型，将由电机本体参数构成的物理模型方程作为可调模型。 该方法系统构成简单，稳定性好，具有较好的实用性和估计精度，但依赖电机本体参数，需要已知比较精确的本体参数，近年也多采用在系统中加入在线辨识电机参数算法的技术。

图6 模型参考自适应法控制结构Fig.6 Model reference adaptive control structure

模型参考自适应的控制算法中，参考模型和可调模型采用相同的电压物理量输入。 在可调模型中，先根据输入电压和估算的电机转子位置，计算出电流输出，然后与参考模型实际采集的电流值进行实时比较，将两者误差通过自适应算法，调节系统输入使得计算估计值趋向实际系统值，即使得估计电机转子位置更加接近真实转子位置。 文献[13]通过该方法进行试验，测得稳态下电机转子位置角估计最大误差为±4°。

3.2 滑模观测器法

滑模观测器法控制是一种采用滑模变结构增益进行观测电机转子位置的方法，其系统控制结构如图7所示。 需要构建一个电机运行理想状态的滑模面，通过根据采集的信号与理想值的误差来调整输入，使得运行状态能够保持在理想滑模面上，转子位置参数观测误差逐渐衰减为零。

图7 滑模观测器法控制结构Fig.7 Control structure of sliding mode observer method

在两相静止坐标系下，两相电流状态的滑模观测器方程为

采用滑模观测器的控制系统有较好的适应性和稳定性，但是这种算法计算量较大，不适用于低成本控制器，并且会引入静态扰动。 许多学者对滑模观测器法提出一系列改进，如：文献[14-15]提出结合饱和函数和S 型函数的滑模观测器； 文献[16]在滑模观测器后加入锁相环进行转子位置估计，效果很明显。

3.3 扩展卡尔曼滤波法

扩展卡尔曼滤波法的永磁同步电机无位置传感器控制是采用最优线性估计法，其控制框架如图8所示。

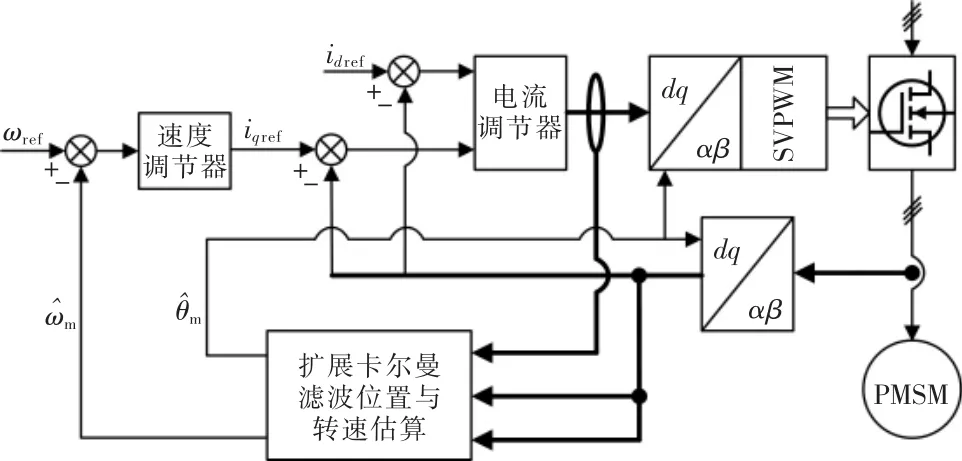
图8 扩展卡尔曼滤波法控制结构Fig.8 Control structure of extended Kalman filter method

这种方法使用含噪声的信号对永磁同步电机的动态系统进行实时递归，从而获取最优的转子位置和转速估计值。 本质上，扩展卡尔曼滤波法也是一种观测器法，不同的是，该方法不需要构建类似模型参考自适应控制和滑模观测器的模型架构，而更近似于一种随机框架观测。 扩展卡尔曼滤波法的永磁同步电机无位置传感器控制控制精度较高，不依赖电机本体系统参数，还具有卡尔曼滤波的抑制扰动噪声和测量误差干扰的优点。 但是这种方法计算量大，实时性要求高，需要运行在高性能的处理器上。

文献[17]采用基于扩展卡尔曼滤波的无位置传感器算法，在静止坐标系下以电机磁链和转速为观测量，系统抗稳定性比较好。

4 全速度范围运行控制

全速度范围是指永磁同步电机运行在静止、低速、中速和高速状态下运行。 目前，业界尚未有一种单一通用于全速度范围下，并能保持良好运行特性的永磁同步电机无位置传感器控制算法。 行业应用和学术研究目前对于全速度范围下的无位置传感器控制，采用凸极模型法和基波模型法相结合的复合控制法[18]。 复合控制法的起动和低速运行采用凸极模型法，中速和高速运行采用基波模型法，其技术难点在于这2 种控制方法在运行过程中的平滑切换。 采用比较多的有直接切换法和加权平均切换。

文献[19]采用直接切换法，在起动和低速阶段使用脉振高频注入法，而在中高速阶段采用模型参考自适应法。 文献[19]试验用2 种算法，同时对电机转子位置进行观测，切换滞环区间为额定转速范围的10%～20%进行直接切换。

图9 加权平均切换原理Fig.9 Schematic of weighted average switching

文献[20]采用脉振高频注入法和滑膜观测器法结合的复合控制法，如图9所示，将无位置传感器的永磁同步电机运行速度分为低速运行区间、切换过渡运行区间和高速运行区间。 在低速运行区间内使用单独使用脉振高频注入法进行转子位置观测，在高速运行区间内单独使用滑膜观测器法，而在切换过渡运行区间同时使用两种方法，将2 种方法观测结果进行线性加权作为最终结果，试验运行平稳，负载动态性能良好。

5 结语

无位置传感器的永磁同步电机控制技术主要在于转子位置检测和估算。 静止状态下的初始位置检测和低速运行状态下主要依靠电机凸极模型性质。 随着转速增加，凸极模型的注入信号会引起振荡和损耗。 所以在中高速状态下，控制主要依靠电机基波模型的性质，最具代表性的是采用各种观测器对转子位置进行估算，这种方法比较依赖电机本体参数。 全速度范围下的复合控制法的技术主要在于研究如何保证过渡点的平滑切换。 结合当前技术应用和面临的问题，无位置传感器的永磁同步电机控制技术研究趋势可能为：①低转速下常采用的信号注入法改进优化保证电机稳定起动；②在中高速控制算法中加入电机参数自动辨识算法，减小系统的参数敏感性问题； ③在低速和中高速的过渡阶段，保证两种控制算法在切换点的平滑切换。