基于人工路标的AGV识别与定位技术研究
陈 成,钱东海,赵 伟,刘 洋,孙林林
(上海大学 机电工程与自动化学院,上海200444)
近几年来,以人工智能及物联网为代表的新一代技术的迅速发展,人类生产生活的智能化程度日益提高,机器人成为人类生产生活的一大主题。 作为机器人的一个重要分支,自动导引车AGV(automated guided vehicle) 产业的发展迎来了巨大的突破。AGV 作为物流系统和柔性制造系统中的关键子系统,目前应用越来越广泛。 并且,随着计算机视觉技术的不断进步,视觉相关技术越来越多地被机器人领域广泛采用。 在工厂的实际生产中AGV 往往需要在目标点附近进行准确定位,以控制AGV 完成更好的停靠。 基于人工路标的视觉定位算法具有速度快、可靠性高、实现简易等特点,能够顺利地应用到AGV 的定位系统中。 故在此研究了基于人工路标的AGV 识别与定位算法,设计出一种简单实用的人工路标,提出一种鲁棒的基于对数极坐标变换的图像识别算法,利用相机采集到路标的4 个顶点,与世界坐标系下的坐标配对求解出AGV 的位姿,实现AGV 在目标点附近的准确停靠。
1 人工路标的设计与识别
人工路标的设计主要考虑路标的简易美观性、路标识别的准确性、实时性、稳定性以及在复杂环境中的可扩展性。 识别算法需要在复杂环境中也能快速准确地识别以此确保定位的精度。
1.1 人工路标的设计
在此综合考虑人工路标的一系列设计要求和已提出的多种路标设计方案,所设计的人工路标如图1所示。 该路标由三大部分组成:红色的矩形方框、内部的白色背景,以及待识别的目标图案。 将路标的外围方框设置为红色的原因有2 个:①因为在该AGV 应用的工作环境中红色的物体相对较少,标准的红色矩形框结构就更少;②因为红色与其他颜色相较其纯度高,散射强度小,明度低,保证了AGV 在不同距离下识别的准确性。内部设置成黑白两色,能够形成强烈的明暗对比,有助于图案的识别。

图1 人工路标Fig.1 Artificial road signs
1.2 人工路标的识别
人工路标的设计完成后,根据路标的一系列特征使其能够在图像中被准确的定位与识别。 通常,路标在图像中的形状、尺寸等会发生很大的变化,使得识别的难度增加不少。 为了在发生尺度变化以及旋转变化的情况下都能准确地识别路标并确定位置,在此提出了一种鲁棒的路标识别方法。 其主要的算法流程如图2所示。
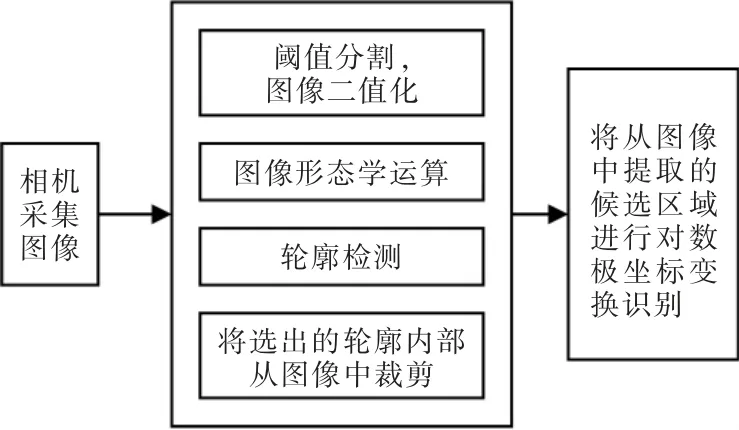
图2 路标检测算法流程Fig.2 Flow chart of road sign detection algorithm
采用基于阈值的分割算法,对相机采集到的彩色图像进行分割。 彩色图像空间有很多种,在此选择在RGB 颜色空间对图像中的红色区域进行分割。采用的r,g,b 计算值为
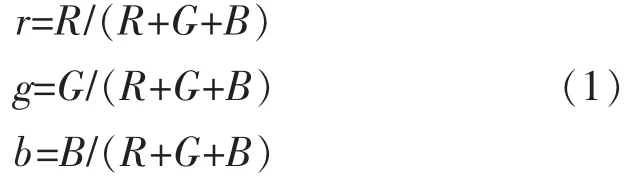
式中:R,G,B 为图像在各颜色空间的亮度值。 计算出r,g,b 的值后,对图像进行二值化,选择r>0.4,g<0.3,b<0.3 时的像素点的值置为255,其余的为0。多次试验证明,该方法对光照强弱不敏感且计算简单,获得的二值化图像如图3。图像中的白色部分即为原图像中的红色区域,黑色则为其他区域。 为了去除图像中的噪声并平滑候选区域,再将二值化图像进行形态学开运算。

图3 分割前后的路标阈值Fig.3 Road sign threshold before and after segmentation
由图可见,经过分割的图像,彩色图像中的红色部分转化为白色,其余部分为黑色。 然而,环境中除路标以外,还可能存在一些其他区域是红色的,因此可以通过轮廓来区分路标与其他干扰区域。
观察路标中红色方框的轮廓是2 个四边形,外围的四边形内部包含另外一个四边形。 通过轮廓检测算法对图像进行轮廓检测,寻找图像中所有的封闭轮廓,此时检查出的轮廓为光滑的曲线,需要对每个轮廓进行多边形拟合,选择形状为四边形且凹凸性为凸的轮廓。 通过余弦定理计算每条边之间的夹角,若其余弦值的最大绝对值小于0.3,则对该轮廓做进一步的判断。 充分利用路标中红色矩形方框的特性,即一个外围四边形轮廓内部再包含一个四边形轮廓,所以目标轮廓一定具有父轮廓,至此准确定位到路标的位置。
找到符合条件内外轮廓之后,利用内轮廓在彩色图像中对路标进行裁剪,对裁剪下来的图片进行投影变换,变换为正方形后采用对数极坐标变换算法识别路标。 对数极坐标变换是将笛卡尔坐标系下的图像转化到对数极坐标系下。 目标经过对数极坐标变换之后,目标的尺度变化与旋转变化转换为极坐标下的横向与纵向平移,这有利于对目标的识别。
笛卡尔坐标系与极坐标系之间的变化关系为

再转换到对数极坐标平面,描述关系为

式中:x,y 为笛卡尔坐标系下坐标;ρ 为直角坐标系下像素点到变换中心的距离即半径长度;θ 为直角坐标系下像素点与变换中心连线与X 轴的夹角即角度;ξ,ψ 为对数极坐标系下的坐标;kξ,kψ为设计参数,用于改进ξ 和ψ 的值域范围;ρmin为进行极坐标变换的最小半径。
对数极坐标变换的变换中心选取的是目标的质心。 该变换有2 个优点:①将目标区域的尺度变化转变为对数极坐标中的上下平移;②目标区域绕其变换中心的旋转相当于沿着ψ 轴平移。 针对优点①例如,一目标以变换中心放大m 倍,其变换公式为

根据式(4)可得,放大m 倍后,相当于沿着ξ 轴平移一段距离。
为了能更好地识别目标,式(4)中引入了ρmin参数,使其开始的位置始终固定,这样放缩导致的平移为零。 此外,为了限定ξ 轴的范围,需要引入参数ρmax,将ξ 轴的值域归一化为[0,kξ],此时变换公式为

其中
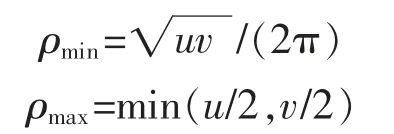
式中:u,v 分别为输入目标图像的长、宽。
由于笛卡尔坐标系与对数极坐标系并非一一对应的关系,为获得较好效果的对数极坐标图像,在变换过程中需要进行线性插值,在此采用双线性插值算法,变化前后的图片如图4所示。

图4 对数极坐标变换前后的图像Fig.4 Images before and after log-polar coordinate transformation
获得对数极坐标图像后,从对数极坐标图像中可以得到代表原始目标特征的直方图。 在对数极坐标图像中,ξ 为像素点到变换中心的距离,所以该图像中同一行的所有像素到变换中心的距离相等。 对对数极坐标图像的每一行像素值为0 的像素点进行统计,就得到一个直方图,该直方图表示原始目标图像中距变换中心相同距离的像素点中像素值为0 的个数。 因为对数极坐标图像具有尺度与旋转不变性,因此统计的直方图也具有该特性。
因此,可以通过极坐标直方图识别从图像中提取的路标,将其与标准路标进行比较。 直方图距离的计算方法有很多种,如相关性比较、卡方距离、巴氏距离等。
在此,测试了不同计算直方图距离的方法,比如L1范数和L2范数、卡方距离。 试验结果表明使用卡方距离会得到较好的结果,所以在系统中采用该方法来计算直方图的距离。
卡方距离源于卡方检验,卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合。 卡方距离应用于2 个柱状图,可以得到这些柱状图所有位置之间的差值的加权平均值,因此可以判断出与目标图案最接近的图案。 直方图i 和j 卡方距离为
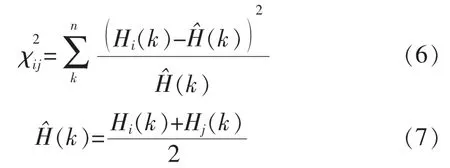
2 AGV 位姿计算
2.1 提取配对点
根据上述对数极坐标变换算法识别路标之后,定位到路标再图像中的位置。 在此选区的配对点是路标的4 个顶点,需要在图像中准确的定位到4 个顶点的位置。 在路标的识别过程中已经获得路标的轮廓,在该轮廓上需寻找路标的4 个顶点,利用路标为正方形的特性,在图像中都会是一个四边形。具体方法如下:
首先,在从相机获得图像上的4 个顶点A(0,0)、B(u,0)、C(u,v)、D(0,v),其中u,v 分别为图像的长和宽,原点位于图像的左上角,依次计算出4 个直线方程:过A 点斜率为-1,过B 点斜率为1,过C 点斜率为-1,过D 点斜率为1。
已知4 个直线方程依次选取路标轮廓上距离各个直线方程最近的点,获得4 个点的坐标,此时可以分为2 种情况讨论:一是4 个点即路标的4 个顶点坐标;二是4 个顶点不是路标的4 个顶点。 判断4 个点为路标的4 个顶点的具体方法如下:
先计算上述4 个点组成四边形的面积,与路标轮廓计算出来的面积相比较。 若4 个点组成四边形的面积与由路标轮廓所围区域面积之比约为1,则选出的4 个顶点即为路标的4 个顶点。 如果选出的4 个顶点并非路标的4 个顶点,其组成四边形的面积与由路标轮廓所围区域面积之比明显小于1,则此时的4 个顶点不是路标的4 个顶点。 一般情况以离外围4 条直线最近的点为路标顶点,具体如图5所示。
若出现第1 次取得的4 个顶点并非路标的顶点,则重新进行选。 在图像坐标系下,求得图像4 条边的直线方程分别为x=0,y=0,x=u,y=v,计算路标轮廓中与这4 条直线距离最近的点,获得的点即为路标的4 个顶点。 此种情况选择离图像4 条边最近的点为路标的顶点,如图6所示。

图5 离外围四条直线最近的点作为路标顶点Fig.5 Points closest to four peripheral lines serves as the signpost vertex

图6 离图像四条边最近的点作为路标顶点Fig.6 Points closest to four sides of the image serves as the signpost vertex
得到路标的4 个顶点之后,4 个顶点在图像坐标系下的坐标就确定了。 还需要一组世界坐标系下的坐标才能求解出AGV 的位姿。 为了使算法更加简单,以路标的中心为原点建立世界坐标系,已知路标的边长,可以得出路标的4 个顶点在世界坐标系下的坐标。 综上,由所获得4 对3D-2D 的匹配点,可以求解出AGV 的位姿。
2.2 解算AGV 位姿
根据二维图像坐标系下的点与三维相机坐标系下的点之间的对应关系,求解位姿通常被称之为PnP(Perspective-n-Point),求解PnP 问题的方法通常有P3P,直接线性变换,EPnP,UPnP,非线性优化,等很多种。在此分别使用P3P,EPnP 和直接线性变换。对比发现,使用EPnP 算法计算的位姿结果误差最小,能够实现较好的精度要求,因此选择EPnP 为位姿求解算法。
由于AGV 在结构化的工厂环境中运行,在平坦的地面上行进,设置相机坐标系与以路标中心为原点的世界坐标系在同一个平面,通过EPnP 算法求解出相机的位姿之后,分解得到旋转矩阵R 和平移矩阵t,综上计算出相机与路标中心的水平距离以及角度就完成了AGV 的定位。
3 试验结果与分析
路标的设计与算法密切相关,不能选择其中之一进行验证,需要将所设计的路标与算法相结合进行验证。 为了验证所提方法的准确性,将路标贴于墙上,并且调节相机光心与路标中心置于同一水平面上。 试验设备如下:相机——普通摄像头,1000万像素,分辨率为1920×1080;试验平台——Intel i5-4200u 处理器,8 GB 内存(算法主要使用C++实现,在VS 2015(Visual Studio)环境下编译);人工路标尺寸——试验所用路标的大小为135 mm×135 mm;一些其他的固定测量设备。
试验中主要有路标坐标系、相机坐标系、AGV坐标系,各坐标系之间的主要关系如图7所示。
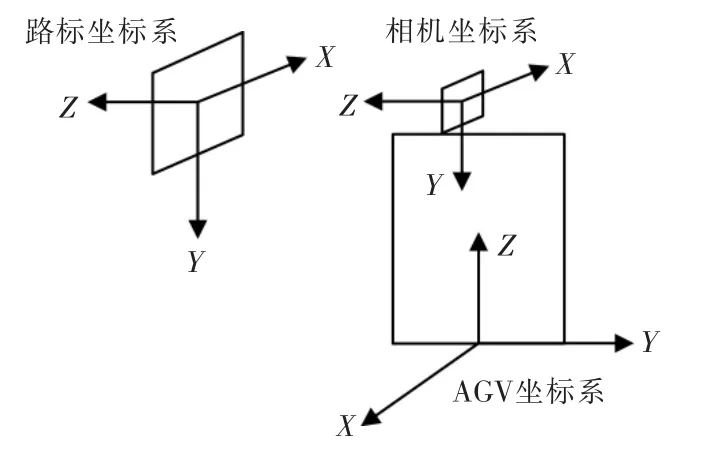
图7 各坐标系之间的关系Fig.7 Relationship between coordinate systems
在此重点关注距离误差和角度误差,在不同距离和不同角度下拍摄路标(如图8所示),获取图像,计算路标与相机之间的相对位姿,计算出相对距离以及角度即可完成相机相对于路标的定位。
图8 在不同距离和不同角度下拍摄路标Fig.8 Shoot road signs at different distances and angles
获取到在不同距离下的误差,以及不同角度下的数据,主要是相机到路标平面的距离及角度2 个数据,每个位置采集5 张图像,估计相机与路标的相对位姿,计算得出距离误差以及角度误差的折线图,结果如图9所示。

图9 人工路标定位误差Fig.9 Error of artificial road sign positioning
由试验结果可知,当距离小于1 m 时误差稳定在一个较小的值,大于1 m 时误差显著增加,但是依旧属于可接受范围;总体的角度误差在±1.5°以内。因此该算法总体具有较好的准确性与稳定性。
4 结语
结构化的工厂环境中,AGV 到达目标点附近时在需要调整位姿后才能准确停靠。针对这种情况,设计了一种简单美观人工路标,用于AGV 在工厂环境中的定位; 提出了一种快速有效的人工路标识别算法,具有尺度不变性与旋转不变性,识别准确等特点。使用单目相机识别路标后,定位路标的位置取得4个顶点在图像坐标系中的坐标,利用已知世界坐标系下的顶点坐标,使用EPnP 算法求解AGV 的位姿,为控制系统提供定位数据。试验结果表明,该算法能有效地识别图像中的路标,并且准确求解出AGV的位姿,能够有效地实现AGV 的定位。 该算法对硬件要求低,系统简单,因此具有很高的实用价值。

