晶格格林函数在位错多尺度模拟中的应用*

刘凤华，李 微，刘晚果

(1 黔南民族师范学院物理与电子科学学院，贵州 都匀 558000；2 黔南民族师范学院化学化工学院，贵州 都匀 558000)

位错是材料中一种重要的结构缺陷，材料的力学性能及其他特性均与位错的几何特征和运动行为有着密切联系。理论上位错芯结构的精确性是影响材料力学性能计算和预测的一个关键点，材料的电子结构及弹性行为均对位错有着很强的敏感性。因此，有必要在原子尺度上对位错进行电子结构的研究。

从宏观上，经典连续介质理论已经可以成功地处理位错的远程应力场问题，在这个尺度上，我们需要的计算量较小；但是在位错核心区原子畸变严重，电子效应明显，因而需要采用精确的计算方法来描述这个尺度上的物理现象，我们一般采用的是密度泛函(DFT)计算方法。由于位错长程应力场的存在，并且在垂直于位错线的平面内对称性已被破坏，因此DFT计算中的周期性边界条件已不适用于含位错体系的模拟。为了克服这一问题，有关位错的DFT计算一般都采用位错偶极子的模型结构[1-2]，构造出的位错偶极子可以将其应力抵消掉这样就可采用周期边界条件，但是这种方法明显忽略了位错远程应力场信息。而多尺度-跨层次方法摒弃了只依赖单一尺度的计算观点，通过耦合量子力学区域和连续介质区域的物理量得到位错的远程应变场，进而实现了对位错的直接模拟。

多尺度现象及相关理论方法是复杂物质体系研究中重要的科学问题[3-4]。多尺度方法的最初应用开始于20世纪70年代，Martin Karplus等[5]将量子化学和分子动力学相结合来研究酶的反应机制，通过计算模拟得到了在复杂系统中比传统实验更精确的预测结果，节省了大量的时间和经济成本。而Martin Karplus等三人也因此获得了2013年的诺贝尔化学奖。这也说明了在材料的研究进程中，多尺度方法的应用越来越收到人们的重视。尤其近几年在材料基因组思想的影响下，采用多尺度方法模拟含缺陷体系已成为材料设计的一种主要理论研究手段。通过多尺度模拟，可以将材料的宏观特性和其微观结构有机结合起来，找出影响材料宏观特性的微观机制，更有效促进材料的研发进程。

1 多尺度模拟方法

多尺度方法的根本目标是发展有效方法，将不同尺度上的相关物理量耦合起来。根据耦合的强弱，多尺度算法可分为串行式(sequential)与并行式(concurrent)两大基本类别[6]。在国内，王崇愚课题组最先开始了串行多尺度方法的研究，将第一性原理计算出的物理量，通过解析传递的方式得代入到经典弹性理论公式中，从而得出位错的宏观攀移速度特性，并且该结果和x射线实验结果符合较好[7-8]，这也说明了该方法的可行性，但是这种方式只适用于尺度间耦合较弱的情况。并行多尺度一般的处理方法是将模拟体系划分为不同尺度层次，每个层次上采用自己特定的处理方法，多个尺度上的计算同时进行，它适合于尺度间变量耦合比较强的情况。并行多尺度算法大致可以分为三大类，其中一类是基于能量耦合的方法[9-13]，通过构造全局的能量泛函得出相关物理量。MAAD(Macroscopic atomistic ab initio dynamics)方法是此类算法中一种典型算法，其基本思想是通过构造整个系统的哈密顿量Htot同时进行量子、原子以及宏观尺度的计算，通过对总哈密顿的求导来求得系统的速度、加速度、轨迹及系统的构型[14]。但是这种方法很难应用到金属体系中，这限制了该方法的应用。另一类算法是Nair等[15]发展的QM-CAD (Quantum Mechanics-coupled atomic discrete dislocation)以位移为耦合条件的多尺度方法，和其他多尺度方法中的区域划分有所不同，在该方法中QM和过渡区的原子交界处多了一层界面原子，在计算中保持过渡区原子固定，只对QM区和界面原子做第一性原理计算，以得到的界面原子的位移作为边界条件，由离散位错本征方程确定出过渡区原子位移。第三类则是基于力参量耦合的方法，像Buehler等发展的量子力学作用力场与 Tersoff 经验力场相结合的耦合模式[16]，还有Payne 发展的LOTF(Learn on the fly)方法[17-18]，该方法主要特点是分子动力学计算中需要的势参数，由第一性原理计算结果进行拟合，将得到的分子动力学的分子构型选取量子力学部分做DFT计算，再拟合新的势参数做为下一次计算的势函数；由于过渡区原子上的力不参与势函数的拟合，因此避免了在QM/MM(Quantum Mechanics/ Molecular Mechanics)边界上力不匹配的问题。分子动力学和第一性原理迭代弛豫的最终结果是体系合力为零且满足动量守恒。但是基于力耦合的多尺度方法普遍的一个问题是在弛豫过程中体系很难达到平衡状态。

考虑到材料中位错核心区域和远程应变场对计算精度的要求不同，Sinclair 等[19]在晶格格林函数的基础上发展起来柔性边界条件的多尺度方法，这是一种典型的基于力耦合的多尺度方法。柔性边界条件的引入就是为了消除原子模拟中在边界上所产生的不匹配力现象。其处理方法是将含缺陷体系在空间尺度上分成三部分，用一个很小的原子区域来模拟复杂的缺陷结构，并将原子区和外部弹性区之间的力弛豫掉，而格林函数则充当了原子区和弹性区之间的“桥梁”。不同于其他位错多尺度模拟方法像有限元法[13]和经验势场法[20]，该方法将缺陷的局域应变场和长程应力场耦合起来正在适用于越来越多的材料模拟中。

2 晶格格林函数

为了反映晶体中由于点缺陷的存在而引起的位移场变化情况，Madrdudin[21]于1963年提出了晶格格林函数(LGF)的概念。当初对晶格格林函数定义为：于Born-von Karman边界条件基础上，取声子格林函数在频率趋于零时的极限值，点缺陷所产生的晶格畸变位移依赖于该缺陷对晶体所施加的力和晶体的力常数矩阵。

在简谐近似的理论下，晶体中原子在离开平衡位置位移u(l) 时体系能量为[22]：

(1)

式中Φ0为体系处在平衡状态下的能量，φαβ(l,l’)为两原子l和l’间3×3力常数矩阵，α,β=x,y,z：

(2)

(3)

(4)

在实空间晶格格林函数表示的是力常数矩阵的逆：

G(0)=(Φ)-1

(5)

其物理意义是当单位大小的力沿β方向作用在原子l’上时，周围l原子在α方向上所产生的位移大小。当力fβ(l’)作用在原子l’上时，该力对周围原子l所产生的位移可通过格林函数表示为：

(6)

所以，如果基体相的晶格格林函数可以确定，那么根据缺陷所产生的力，就可以很容易地求出缺陷所引起的晶格畸变位移场。因此，晶格格林函数的精确度决定着计算模拟的效率和精确性。早期的晶格格林函数的解析求解只限制在立方晶系金属中[21,23]，由于含缺陷特别是位错体系的格林函数计算起来特别复杂，一般的方式是用完整晶体的晶格格林函数来近似含缺陷体系的格林函数[24]，这无疑是增加了体系收敛过程中的迭代步数。近几年含缺陷体系的LGF[25-26]，特别是Tan等[27]计算出了含位错体系的晶格格林函数，大大降低了在弛豫过程中的迭代次数并提高了计算精度。

3 晶格格林函数在位错模拟中的应用

晶格格林函数最初是应用于立方晶系的点缺陷的模拟计算中[21]，通过计算含点缺陷体系的格林函数来模拟点缺陷所产生的位移场。Tewary等[28]将弹性格林函数和晶格格林函数结合，对Si-Ge(001)量子阱中的点缺陷(间隙或空位)进行了多尺度模拟计算，从数值上得出了点缺陷附近的离散芯结构以及其所产生的应变场。

早期的晶格格林函数计算体系和范围较小，为了更好地模拟晶体中的缺陷结构，S Rao等[29]在进一步发展了此算法，在位错核心区采用原子间相互作用势，实现了在较少原子数的晶胞中位错的计算模拟。为了得到更到的精度，C Woodward[30]采用柔性边界的格林函数方法成功模拟了体心立方金属Mo和Ta中的位错芯结构，分别对不同尺寸的晶胞进行模拟，发现采用柔性边界条件后尺寸较小的晶胞仍能完整体现体系的位错应变场。随后，依据同样的方法，C Woodward得出了具有L10结构的金属间化合物TiAl合金中α/2<110>螺位错的位错芯附近的应变场[31]，从螺位错的位错芯结构推测出螺位错易于发生交滑移，并且还发现该螺位错可以分解出重要的刃位错分量，由此计算出的晶格阻力是测得的单晶TiAl合金中屈服强度的两倍。在面心立方金属Al中，采用格林函数对Al中的螺位错和刃位错也都有相关计算[24]，结果显示位错芯宽度均和实验符合很好，在此位错芯基础上，Curtin[32]进一步计算了溶质和位错的相互作用，从而实现了理论上Al的屈服强度的预测，这是材料强度预测的一大进步。随着算法的发展，格林函数的求解也由完整晶格格林函数向含缺陷结构的晶格格林函数转变，从而使格林函数多尺度方法更普适于一般缺陷体系，如在含界面结构的体系中，Trinkle等[33]就计算出了在Ti中螺位错和孪晶界的相互作用；以及在具有HCP结构的 Mg金属中，根据柔性边界条件得到了Mg中位错芯结构以及和溶质原子的相互作用能[34]。通过将格林函数应用于不同金属不同结构中的位错线模拟[35-37]，均得到和实验符合较好的结果，这也说明了该方法的可靠性。并且对于核外电子数较多的金属镍，通过格林函数方法[38]也可得到其平衡位错芯结构，且位错芯宽度和其他计算符合很好[35-36]。

4 晶格格林函数在模拟中的计算流程

对于含位错体系，一般将整个模拟晶胞就分成三个区域：位错芯区1，格林函数“桥接”区2和经典弹性理论的连续区3。一般在沿位错线方向采用周期性边界条件，离位错线最近的区域取为位错核心区，最外面为弹性连续区，取真空边界条件。在一区位错芯区，原子错排较大，这时胡克定律不再适用，利用第一性原理计算对该区原子进行弛豫计算；三区为弹性连续区，该部分的处理可采用位错远程场的经典弹性理论；由于在一区和三区原子间，分别采用不同尺度的处理方法，这就会使得在两区的交界处的原子上产生力不匹配的现象，这部分的原子属于二区缓冲区，为了耦合一区和三区之间的力的不匹配，在这一区域上采用晶格格林函数的方法进行弛豫。

图1 格林函数方法中模型的分区图示[29]

如果采用完整晶格的晶格格林函数来处理含位错体系模型，一般的方法是将位错看成是一种微扰，由于完整晶格格林函数和含位错体系的格林函数之间的差别，这就要求在使用完整格林函数弛豫过程中需不断迭代计算过程，图2为其迭代计算流程[39]。

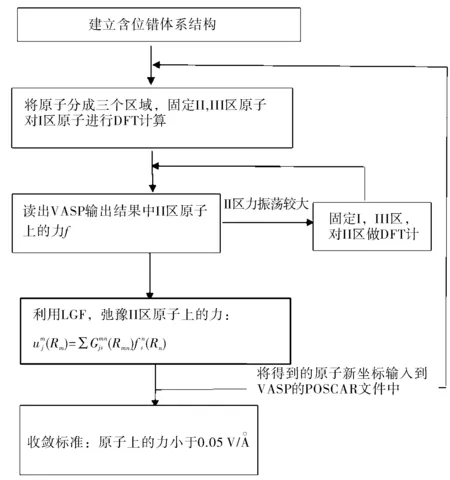
图2 格林函数和第一性原理迭代计算流程图

5 结 语

多尺度算法在材料性能研究中的作用越来越重要。材料基因组计划的宗旨就是在建立一个新的以计算模拟和理论预测优先、实验验证在后的新材料研发文化，从而取代现有的以经验和实验为主的材料研发的模式[40]。以晶格格林函数为“桥接”的多尺度力匹配方法，实现了对位错芯结构的第一性原理计算，为理论预测提供了模型构型基础，正在适用于越来越多的金属材料，发挥着突出作用。