重载列车提载对简支T梁桥动力响应的影响

肖烨 罗小勇

(1.中南大学 土木工程学院，湖南 长沙 410075；2.东华理工大学 土木与建筑工程学院，江西 南昌330013)

我国既有铁路桥涵结构绝大多数采用标准设计，桥梁结构以双片式简支T梁为主，主要为16、20、24和32 m预应力混凝土梁。目前，我国重载铁路主要开行21 t和23 t轴重的运煤敞车，少量开行25 t轴重的专用敞车[1]。为了提高运输效率，我国拟通过对既有线路基础设施进行强化改造，开行30 t及以上轴重的重载货物列车。重载货物列车轴重的提高增加了作用于铁路轨道及桥涵结构上的荷载，从而加大了重载铁路桥梁结构的动力响应，对既有铁路桥梁结构的适应性提出了挑战。目前关于重载列车对桥梁结构动力响应的影响，主要基于现场测试，费时费力，数值仿真计算相对较少。闫晓夏等[2]对24 m和32 m超低高度预应力混凝土简支梁进行了检算，通过对30 t轴重实车试验获取了桥梁结构的动力响应并评估其提载适应性；卫军等[3]通过建立桥梁刚度的时变模型对重载铁路桥梁服役性能进行了评估和预测；郭薇薇等[4]以铁路新型钢-混凝土组合桁架桥为例，采用数值模拟的方法计算分析了桥梁在高速列车作用下的动力响应。Yu等[5]对大轴重重载运输条件下重载铁路桥梁动力响应的随机性进行了研究；刘钰等[6]建立了车桥耦合振动分析模型，研究了跳车情况下桥梁的结构动力响应；Xia、Zhang等[7-8]通过建立车桥耦合振动模型对高速列车车桥动力相互作用进行了深入研究。以上研究主要采取仿真分析与试验相结合的方法，在有限元模型仿真模拟计算中，大多采用静活载加动力系数或移动不变力的简化荷载来模拟列车对桥梁的作用[9]，所建立的动力学模型多为单节车辆，且未考虑车辆轴重提高时车辆技术参数(车辆长度、车辆定距、轴距等)变化对桥梁结构动力响应的影响。

为研究重载列车提载对既有铁路桥梁结构动力响应的影响，作者以应用较为广泛的重载铁路16、20、24和32 m普通高度预应力混凝土简支T梁为例，根据现场实测数据，建立重载列车-轨道-桥梁三维耦合精细化有限元模型，结合我国常用敞车车辆技术参数(车辆长度、车辆定距等)，计算分析重载列车作用下车桥系统的动力响应，探讨列车编组数对桥梁结构动力响应的影响，揭示重载列车提载对既有铁路典型桥梁结构动力响应的影响规律，并对既有铁路典型桥梁进行提载适应性分析，为既有铁路桥梁重载强化改造技术和新建重载铁路桥梁的设计提供参考。

1 重载列车-轨道-桥梁耦合有限元模型

1.1 重载列车车辆模型

车辆系统动力平衡方程可表述为

(1)

(a)正视图

根据调研，我国目前及以后主要重载货物列车的轴重为25.0、27.0、30.0、32.5 t及以上。各重载列车车辆主要技术参数见表1。

表1 重载列车车辆参数Table 1 Parameters of Heavy haul train vehicle

1.2 轮轨接触模型

轮轨接触采用面面接触，车轮为刚体，选取主面为车轮表面，从面为钢轨顶面，轮轨接触关系如图2所示。

图2 轮轨接触关系Fig.2 Wheel-rail contact relation

轮轨接触关系采用Hertz非线性接触[10]和动力学摩擦模型[11]模拟轮轨法向接触力和切向接触力，轮轨法向接触力可表示为

(2)

式中：G=3.86R-0.115×10-8，m/N2/3；R为车轮半径，m；t为时间，s；δZ(t)为t时刻的轮轨间相对压缩量，表示为

δZ(t)=Zw(t)-Zr(t)-Z0(t)

(3)

Zw(t)、Zr(t)和Z0(t)分别为t时刻的车轮位移、钢轨位移和轮轨间位移不平顺值。

轮轨切向接触力可表示为

F=μP(t)

(4)

μ=μk+(μs-μk)e-dcvc

(5)

式(5)中各参数具体数值详见文献[11]。

1.3 轨道-桥梁模型

重载铁路有砟轨道结构由钢轨、扣件、垫板、轨枕和道砟等组成。有砟轨道模型的建立具体可参考文献[12]。

桥梁模型选取朔黄铁路线上16～32 m的普通高度预应力混凝土双片式T梁，按4跨简支梁模型建立，32 m的T梁有限元模型如图3所示，其余从略。梁体、横隔板和桥墩均采用8节点实体单元模拟，两片T梁之间通过横隔板连接；混凝土参数详见文献[13]中参数；支座顶部采用线性弹簧阻尼单元与梁体联结，底部设置为固定约束；垂向和纵向刚度值为109N/m，横向刚度值为108N/m，阻尼值均为6104kN·s/m。

图3 T梁有限元模型Fig.3 Finite element model of T-beam

以轨道-桥梁自身系统动力平衡位置为坐标原点，建立轨道-桥梁系统动力方程为

(6)

将轮轨法向接触力和切向接触力写入方程(1)和(6)的右端项即可得重载列车-轨道-桥梁系统动力方程：

(7)

式中，Fv为车辆与轨道-桥梁系统之间的轮轨相互作用力Fvb,Fb包括车辆自重Fvg和轮轨相互作用力Fbv。

考虑轨道高低和水平不平顺，计算时采用美国五级轨道谱作为不平顺激励源进行输入。采用分离迭代法求解耦合系统的动力方程[14]，车辆系统与轨道-桥梁系统之间通过轮轨接触力平衡条件进行反复迭代实现动力平衡，直至前后两次迭代计算得到的轮轨接触力之间的相对误差百分比小于等于10-4时，判定计算结果收敛。

有研究者认为建立的由三节重车车辆组成的列车模型已基本上能反映重载列车的动力学性能[15]，根据重载列车编组长度的相关研究结果[12]并基于高速列车常采用8节列车编组的情况，本研究建立8节列车编组，建立重载列车-轨道-桥梁三维耦合系统动力有限元模型，如图4所示。

图4 重载列车-轨道-桥梁三维耦合有限元模型Fig.4 3-D coupled finite element model of heavy haul train-track-bridge

2 现场试验及模型验证

2.1 现场试验

为验证有限元模型的准确性，选取朔黄重载铁路线上一座典型32 m多跨预应力混凝土简支梁进行现场试验，选取其中的1跨(2#墩至3#墩)进行测试，传感器位置布置在第2跨的跨中部分，采用安装在桥面上的891型传感器测量桥梁跨中的竖向加速度和横向加速度等。现场测试如图5所示。

(a)桥梁测点布置

2.2 模型验证

C80运营货物列车(25.0 t轴重)以79.6 km/h的速度通过桥梁时的现场测试结果与计算结果见表2，其中跨中加速度响应时程曲线如图6所示。

表2 计算结果与测试结果对比Table 2 Contrast of calculated results and test results

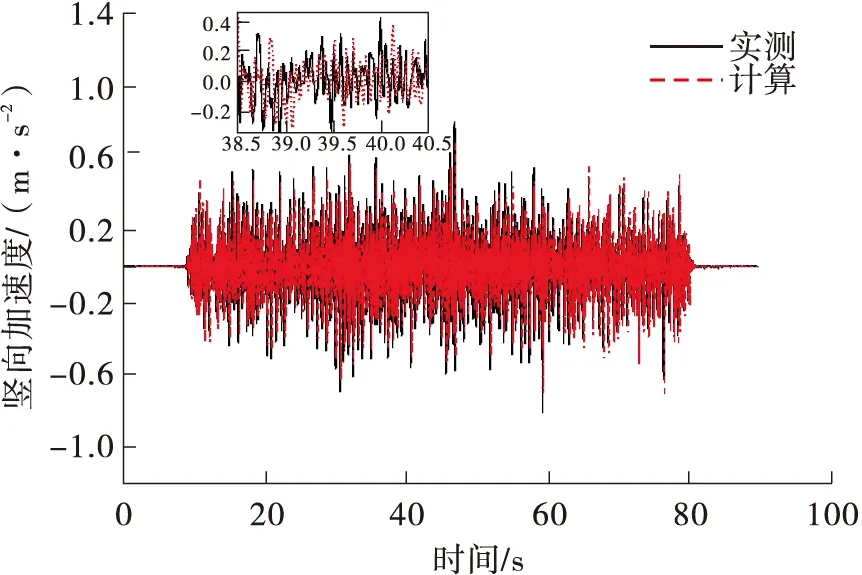
(a)竖向加速度

由表2可知：计算结果与测试结果较为接近，偏差均在5%以内。由图6梁跨中加速度时程曲线对比结果可知：计算与实测所得的梁跨中加速度响应时程曲线形状及幅值较一致，说明计算结果与测试结果基本吻合，从而验证了有限元模型的正确性。

3 列车提载对桥梁动力响应的影响

为了研究重载列车提载(提高轴重)对桥梁动力响应的影响，基于上述重载列车-有砟轨道-桥梁三维有限元模型，考虑货物列车车辆设计技术参数制定了如下两种计算工况。

工况1：选取32.5 t轴重货物列车车型(共8节列车编组)分别装载25.0、27.0、30.0、32.5 t轴重货物以80 km/h匀速通过不同跨度的桥梁。

工况2：采用表1中各轴重货物列车(共8节列车编组)按照轴重等级分别对应装载25.0、27.0、30.0、32.5 t轴重货物以80 km/h匀速通过不同跨径的桥梁。

按照以上两种工况计算各跨度预应力混凝土梁分别在25.0、27.0、30.0、32.5 t轴重作用下的结构动力响应，各跨度预应力混凝土梁的跨中动力响应最大值见表3和表4，限于篇幅仅列出了16 m和32 m跨度桥梁跨中竖向位移(挠度)时程曲线如图7所示。

从表3和表4的梁跨中最大动力响应结果可见：工况1采用相同货物列车车型时，各跨度桥梁的跨中位移响应最大值随着轴重的提高呈近似线性增加；跨中加速度响应最大值随着轴重的提高而有所增大；工况2采用不同货物列车车型时，16、20、24 m跨度桥梁的跨中动力响应最大值均随着列车轴重的提高而逐渐增大，但随着跨度的增加，增幅逐渐减少；32 m跨度桥梁的跨中动力响应最大值随着列车轴重的提高增幅比以上跨度的桥梁要小，其中27.0 t轴重重载列车对32 m跨度桥梁所产生的动力响应最大值比25.0 t轴重略小。分析原因为：此时有2个半节列车车体作用于桥梁上，相当于有多个集中力作用于桥梁，而27.0 t轴重列车的车辆长度和车辆定距比25.0 t对应值大，两者轴距相同，间距不同(27.0 t车辆定距比25.0 t对应值大1 m)，荷载虽有增加，但增加不多，而荷载间距增大时，集中力分布会比较分散，当计算跨度达到一定数值时所产生的荷载效应会比较小，这符合结构力学规律；可见车体长度和车辆定距主要影响跨度较大的桥梁。依此可推断当桥梁跨度很小(小于8 m)时，此时最多只有相邻的两个轮对作用于桥梁，与车体长度和车辆定距无关，仅与轴距有关；由于轴距基本相同，即荷载间距相同，列车对桥梁所产生的竖向位移将随着轴重的提高而显著递增。

表3 工况1的计算结果Table 3 Calculated results of the load case 1

表4 工况2的计算结果Table 4 Calculated results of the load case 2

由图7所示的梁跨中竖向位移时程曲线可见：工况1采用相同货物列车车型时，桥梁的跨中竖向位移均随着轴重的提高呈近似线性增加；工况2采用不同货物列车车型时，由于车体长度和车辆定距的不同，不同货物列车作用在桥梁上的时间和荷载效应不同，各跨度桥梁的跨中竖向位移随着列车轴重的提高而逐渐增大，随着跨度的增加，位移增幅逐渐减少，其中27.0 t轴重的列车对32 m跨度桥梁所产生的竖向位移最大值比25.0 t轴重的列车对应值略小。

(a)16 m跨度桥梁，工况1

通过对比以上两种工况可知，工况2中25.0、27.0、30.0 t轴重列车对各跨桥梁所产生的动力响应均比32.5 t轴重的列车装载相同轴重的货物时大，这是由于32.5 t轴重的货物列车的车辆长度、车辆定距均比25.0、27.0、30.0 t轴重的列车大，对桥梁所产生的动力响应反而小，即装载相同轴重货物时，车体长度和车辆定距较大的车型对中等跨度桥梁产生的动力响应较小。

4 既有铁路典型桥梁提载适应性分析

以16、20、24、32 m预应力混凝土简支T梁为例，采用重载列车-轨道-桥梁三维耦合有限元模型(列车运行速度80 km/h)对桥梁进行提载适应性仿真计算。根据国内外现有铁路桥梁设计规范等文献资料[16-19]，参考国内外铁路桥梁规范确定桥梁评定规范限值(见表5)，得到不同轴重列车作用下各跨度桥梁动力响应结果与规范限值，如图8所示。

表5 规范限值Table 5 Code limits

由表5和图8可知：各轴重列车作用下各跨度桥梁跨中最大竖向加速度、最大竖向位移(挠度)均低于标准限值，满足要求；35.0 t以下各轴重列车作用下16、20、24 m跨度桥梁跨中最大横向位移,25.0 t和27.0 t轴重列车作用下32 m跨度桥梁跨中最大横向位移值均低于标准限值，满足要求。30.0、32.5、35.0 t轴重列车作用时，32 m跨度桥梁横向位移值分别超出标准限值0.31、0.54、0.85 mm，约14.9%、25.9%、40.9%；各轴重列车作用下24 m跨度桥梁跨中最大横向加速度低于标准限值，满足要求；25.0 t轴重列车作用下16 m跨度桥梁跨中最大横向加速度低于标准限值，满足要求，27.0、30.0、32.5、35.0 t轴重列车作用时，其值分别超出标准限值0.08、0.61、0.81、1.03 m/s2，约5.7%、43.6%、57.9%、73.5%。25.0、27.0 t轴重列车作用下20 m和32 m跨度梁跨中最大横向加速度低于标准限值，满足要求；30.0、32.5、35.0 t轴重列车作用时，20 m跨度梁其值分别超出标准限值0.20、0.38、0.56 m/s2，约14.3%、27.1%、40.0%，32 m跨度梁其值分别超出标准限值0.05、0.07、0.15 m/s2，约3.6%、5.0%、10.7%。可见当列车轴重达到27.0 t及以上，16 m跨度桥梁横向加速度超出规范限值；当列车轴重达到30.0 t及以上时，既有铁路典型20 m跨度桥梁横向加速度，32 m跨度桥梁横向位移、横向加速度等横向振动响应偏大，超出了规范限值，应对桥梁进行横向加固。

图8 不同轴重列车作用下桥梁动力响应计算结果与规范限值对比Fig.8 Contrast of calculated results and code limits under different train axle load

5 结论

(1)采用相同货物列车车型时，各跨度桥梁的跨中位移响应最大值均随着轴重的提高呈近似线性增加；各跨度桥梁的加速度响应最大值随着轴重的提高而有所增大；采用不同货物列车车型时，列车车体长度和车辆定距对跨度较大桥梁的影响较大。16、20、24 m跨度桥梁的跨中动力响应最大值均随着列车轴重的提高而逐渐增大，但随着跨度的增加，增幅逐渐减少；32 m跨度桥梁的跨中动力响应最大值随着列车轴重的提高增幅比以上跨度的桥梁要小，其中27.0 t轴重重载列车对32 m跨度桥梁所产生的动力响应最大值比25.0 t轴重对应值略小。

(2)装载相同轴重货物时，车体长度和车辆定距较大的车型对16 m以上跨度的桥梁所产生的动力响应较小；当桥梁跨度很小(小于8 m)时，重载列车对桥梁所产生的动力响应与车体长度和车辆定距无关，仅与轴距有关，动力响应数值将随着轴重的提高而显著递增，因此在既有线重载列车提载时应特别重视对小跨度桥梁的维护和加固。

(3)当列车轴重达到27.0 t及以上，16 m跨度桥梁横向加速度超出规范限值；当30.0 t及以上轴重列车通过桥梁时，既有铁路典型20 m跨度桥梁横向加速度、32 m跨度桥梁横向位移和横向加速度等横向动力响应偏大，不满足规范要求，需对桥梁进行横向加固。