基于毛细压力对数的HAM模型改进

孟庆林 李复翔 李琼

(华南理工大学 建筑学院,广东 广州 510640)

受热带海洋环境影响，我国南海岛屿地区全年高温高湿，太阳辐照极其强烈，在建筑热工分区上体现出极端热湿气候的特点[1]。该气候特点使得当地建筑承受着远高于大陆地区的热湿压力，墙体在温度、湿度以及空气压力梯度下发生强烈的传热、传湿及空气渗透过程(简称HAM)，导致该地区的建筑能耗居高不下，室内舒适度欠佳。解决这一问题的关键是建立能够准确描述该地区HAM过程的数学模型并以此指导围护结构设计。

目前，关于南海地区热湿耦合传递的研究非常有限。董浩[2]以相对湿度为湿驱动势建立模型，并对马尼拉气候下的墙体内部热湿分布进行了模拟分析。罗戴维等[3-4]则比较了不同湿驱动势在该地区的适应性，以毛细压力作为湿驱动势建立了热湿耦合传递模型。然而，上述研究均忽略了空气渗透过程对热湿传递的影响，所以在进行能耗计算[5-6]、墙体热湿状况分析[7]时会出现较大偏差。此外，两模型均未在室外边界条件中使用南海地区实际气象数据，缺乏实际工况下的验证和计算。刘晓燕等[8]从微观角度建立了包含空气渗透的热湿耦合模型，但该模型的方程参数难以确定且室外边界条件无法反映非稳态逐时变化的特点。刘向伟[9]以KUNZEL研究为基础，针对夏热冬冷地区建立了包含空气渗透的热湿耦合传递模型，并采用基准案例对模型准确性进行了验证。由于南海地区极端热湿的气候特点，文献[8-9]中模型是否适用需要进一步研究。模型适用性的主要影响因素是建立模型时所选择的湿驱动势，包括水蒸气分压力[10]、体积含湿量[11]、相对湿度[12]、水的化学势[13]、毛细压力[14]等，这些物理量都被选作湿驱动势来建立模型。文献[15]就不同湿驱动势的优缺点进行了简要的比较分析，大致指出了各自的适用范围，但缺乏不同驱动势的计算效率及准确性分析，由于南海地区独特的气候特征，建立模型时必须对此充分考虑，选择合适的湿驱动势。

基于上述分析，为全面准确地计算该地区建筑墙体内的热湿分布，需要建立一个对南海岛屿气候有良好适应性且考虑空气渗透过程的HAM模型。为此，本研究参照相关文献，通过使用毛细压力对数作为湿驱动势对热湿耦合传递方程进行了重新推导，建立了包含空气渗透过程、以室内外空气参数为边界条件的建筑墙体瞬态热湿耦合传递模型，使用基准测试验证了新建模型的准确性，并与已有模型在计算效率、准确性方面进行了对比分析；发现新建模型在静态边界条件下能有效缩短收敛时间。最后考察了模型在南海实际气象条件下的计算表现。

1 模型建立

由于南海地区常年高温高湿，太阳辐射强烈，且经常出现强降雨，使得墙体可能面临十分剧烈的热湿状态变化，在选择湿驱动势时必须对此加以考虑。近期，有学者探讨了毛细压力对数(以下简称Lpc)作为湿驱动势的优点：从数值计算的角度看其变化平稳，稳定性较高，适合一些极端工况如突然受潮或雨水侵袭[15];Portal等[16]认为Lpc作为湿驱动势适合非等温或者包含强烈热湿源(如强太阳辐射和雨水)的工况，文献[3]也曾提到使用Lpc可提高模型准确性。可以看出，上述优点对于极端热湿气候下可能出现的工况很有针对性，因此，本研究将采用LPc作为湿驱动势建立HAM模型。

1.1 湿控制方程

多孔材料中湿分是以蒸汽或液态水的形式进行传递，依据质量守恒定律，单元体湿分迁移、储存过程可表示如下：

(1)

jv=jv,d+jv,c

(2)

式中：w为材料的体积含湿量，kg/m3，可由材料等温吸放曲线计算；t为时间，s；jl、jv分别为液态水和水蒸气传递速率，kg/(m2·s)；水蒸气传递包括湿度梯度引起的扩散项jv,d和随空气流动发生的对流项jv,c。

根据达西定律和菲克定律，jl和jv,d可由下式计算：

(3)

(4)

式中：Dl是液态水传导系数，kg/(Pa·m·s)；pc为液态水毛细压力，Pa；x为梯度方向距离，m；δv为水蒸气传导系数，kg/(Pa·m·s)；pv为水蒸气分压力，Pa。

将材料内部湿空气按照理想气体处理，式(4)中水蒸气分压力梯度可以写成相对湿度φ和水蒸气饱和分压力ps的函数，而ps是湿空气温度T的函数，上述关系可表示如下：

(5)

依据开尔文关系，毛细压力pc与相对湿度φ之间存在以下换算关系：

pc=-ρwRvTlnφ

(6)

(7)

式中:ρw为液态水密度，1 000 kg/m3；Rv为水蒸气气体常数，462 J/(kg·K)；φ为相对湿度。

为方便后续统一方程中驱动势，在此引入毛细压力对数Lpc的计算公式：

Lpc=lgpc

(8)

由于温度变化对于含湿量的影响可忽略不计，体积含湿量成为相对湿度的单值函数，即材料的等温吸放曲线，由此式(1)左边可简化为

(9)

分别将式(8)代入式(3)，将式(6)-(8)代入式(4)，可得液态水和水蒸气传递速率的计算公式如下：

(10)

(11)

对于空气渗透产生的对流项jv,c，其计算公式如下：

jv,c=xvja

(12)

式中，xv为湿空气比湿，kg/kg；ja为空气的质量流量，kg/(m2·s)。依据泊肃叶定律，ja可表达为

(13)

式中：ka为材料的空气渗透率，kg/(Pa·m·s)；pair为空气压力，Pa。

在建筑物理领域中，由于空气渗透过程缓慢，且温度变化不大，所以空气可视为不可压缩流体，根据连续性方程有

(14)

式中：ρa为空气的密度，kg/m3；ε为材料的孔隙率。由式(14)可知，当ka一定时，空气压力梯度将唯一决定微元体内的空气流量。

式(12)中，依据理想气体状态方程湿空气比湿xv的计算公式如下：

(15)

式中：mv为水蒸气质量，kg;mm为湿空气质量，kg；pa为大气压强，1.01×105Pa;Ra为干空气气体常数，287 J/(kg·K)。

将式(15)代入(12)，可得jv,c的计算公式如下：

jv,c≈0.62×10-5pvja

(16)

将式(10)、(11)、(16)代入式(1)后可得湿控制方程为

(17)

1.2 热控制方程

多孔建筑材料内部的能量平衡除了受材料热传导影响外，还受到材料内部液态水迁移、水蒸气迁移和空气渗透过程的影响，根据能量守恒定律，微元体内热量迁移、储存过程可表示如下：

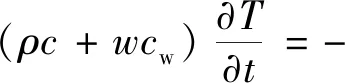
(18)

式中：ρ为干材料密度，kg/m3；c为材料比热,J/(kg·K)；cw为液态水定压比热容，4 200 J/(kg·K);qc、ql、qv、qa分别表示材料导热量，液态水迁移过程、水蒸气迁移过程、空气渗透过程带来的热量，W/m2。

与水蒸气的潜热相比，液态水和水蒸气的显热可以忽略不计，忽略ql和qv的显热部分后，各热流密度的计算公式如下：

(19)

qv=jv,dL

(20)

(21)

式中：λ为材料的导热系数，W/(m·K);L为水蒸气汽化潜热，J/kg；cp,a为空气的定压比热容，J/(kg·K)。

将式(19)-(21)代入式(18)可得热控制方程如式(22)所示：

(22)

至此，以毛细压力对数为湿驱动势的包含空气渗透过程的热湿耦合传递模型(以下简称LPc模型)建立完毕。

1.3 边界条件

分析可知，室外热流qe与以下5种方式有关:

qe=he(Te-Tse)+qa,s+ql+qr+qrain

(23)

各分项分别可按下式计算：

qa,s=cp,aja(Te-Tse)

(24)

ql=βeL(pva-pvs)+0.62×10-5Lja(pva-pvs)

(25)

qr=αqsol

(26)

qrain=jraincw(Train-Tse)

(27)

室外湿流ge主要有湿空气对流、渗透和降雨增湿3种途径，可表示如下：

ge=βe(pva-pvs)+0.62×10-5ja(pva-pvs)+jrain

(28)

式(24)-(28)中:he为外表面对流换热系数，W/(m2·K)；Te为环境温度，Tse为外表面温度，K；qa,s是表面空气渗透所带来的热流，W/m2；qr为外表面吸收的太阳辐射，W/m2；ql为潜热项所带来的热流,W/m2；qrain为雨水降温效应，W/m2；βe为外表面质交换系数，kg/(Pa·m2·s)；pva和pvs为环境和外表面的水蒸气分压力，可由饱和水蒸气公式和室外相对湿度φe求得，Pa；α为太阳辐射吸收系数，qsol为垂直面所接收的太阳辐射，W/m2；jrain为外表面所吸收的雨水量，kg/m2；Train为雨水的温度，K。

分析可知，室内侧热流、湿流的变化主要是由内表面与室内空气发生对流传热、传湿以及空气渗透过程引起的，热湿边界条件表示如下：

qi=hi(Ti-Tsi)+cp,aja(Ti-Tsi)+

Lβi(pvi-pvis)+0.62×10-5Lja(pvi-pvis)

(29)

gi=βi(pvi-pvis)+0.62×10-5ja(pvi-pvis)

(30)

式(29)-(30)中:hi为内表面对流换热系数，W/(m2·K)；Tsi为内表面温度，Ti为室内温度，K；βi为内表面对流传质系数，kg/(Pa·m2·s)；pvi和pvis分别为室内水蒸气分压力和内表面水蒸汽分压力，由饱和水蒸气公式和室内相对湿度φi求得，Pa。

2 模型求解

由于新建模型方程组的高度耦合和非线性，手动求解具有较大的难度，本研究采取Comsol Multiphysics中系数型偏微分方程接口(PDE)实现模型的求解，该接口利用有限元法对控制方程组及边界条件进行离散，大大简化了求解过程[17]。同样的求解方法也用于下文进行对比的相对湿度驱动势HAM模型和毛细压力驱动势HAM模型，两模型方程如下所示。

相对湿度HAM模型(以下简称RH模型)[18]：

(31)

式(31)中，ξ为建筑材料等温吸附曲线的斜率，kg/m3。

以文献[4]中模型为基础，可得毛细压力HAM模型(以下简称Pc模型)：

(32)

3 新建模型验证及对比

本研究采用国际公认的HAMSTAD项目[19]来进行上述模型的验证，选用具有分析解的案例2和同时涉及传热、传湿和空气渗透的案例3来验证上述模型的准确性，并在验证过程与RH模型和Pc模型进行了对比。

3.1 具有分析解的基准案列2

案例2分析了单层各向同性墙体的等温干燥过程，墙体气密性良好，墙体结构及边界条件如图1所示。在初始时，墙体与周围环境保持热湿平衡，温度为20 ℃，初始含湿量为84.77 kg/m3(φ=95%，Lpc=6.841 57 Pa，pc=6.943 4106Pa)。案例工况开始后，周围环境的相对湿度突然发生变化，室外相对湿度变为45%，室内相对湿度变为65%，而环境温度保持不变，仍为20℃。在湿度梯度下，墙体向周围环境放湿，其内部湿分重新分配。该案例持续1 000 h，要求输出第100、300、1 000 h的墙体内部含湿量分布，与分析解结果对照。模拟采用的详细热湿物性参数见文献[19]。

图1 HAMSTAD验证实例2中各向同性墙体结构Fig.1 Configuration of the homogeneous wall in HAMSTAD benchmark 2

由于墙体气密性良好，因此该基准案例不涉及空气渗透过程，3种模型的网格均设置为极细化，需要求解402个自由度(4个内部自由度)，并将瞬态求解器的相对容差设置为1×10-11。3种模型的计算结果如图2所示，计算结果基本重合且均与分析解高度吻合，但在计算时间上，求解LPc模型需要8 s，求解Pc模型需要11 s，而求解RH模型最慢需要12 s，可以看出对于基准测试2所对应的工况，使用Lpc作为湿驱动势可以有效加速模型收敛，并且取得很高的准确性。

图2 3种模型计算结果与基准案例2分析解比对Fig.2 Comparison between the results of three models and analytic results of benchmark 2

3.2 包含轻质墙体空气渗透过程的基准案例3

基准案例3测试了200 mm厚轻质墙体在室内外存在空气压差的条件下发生的热湿迁移过程，墙体机构及边界条件参数如图3所示。室内温湿度分别为20 ℃、70%，室外温湿度分别为2 ℃、80%，在整个过程中均保持不变，内外表面对流换热系数均为10 W/(m2·K)，内外表面对流传质系数分别为2×10-7s/m和7.38×10-12s/m。空气的渗透方向如图4所示，室内外压差p>0时，空气由内向外流动，p<0时，空气由外向内流动，模拟持续100天，在第20-21天间，p由正变负，其他详细的热湿物性参数见文献[19]。

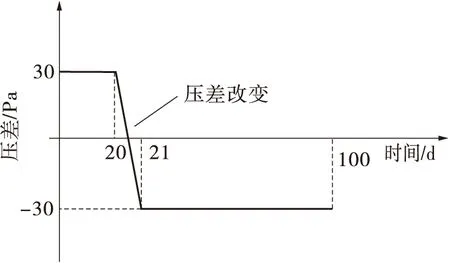
图4 基准案例3的空气压差变化Fig.4 Air pressure variation of benchmark 3

图3 基准案例3的几何结构及边界条件Fig.3 Geometry and boundary conditions of benchmark 3

3种模型的网格均设置为极细化，需要求解402个自由度(12个内部自由度)，求解精度设置与案例2相同。分别取墙体0.05 m、0.19 m的A、B两处的温度和体积含湿量模拟结果与参考结果进行比对，参考结果取自参与HAMSTAD项目研究机构(包括CTH、TUD(荷兰)、Technion(以色列)、KUL(比利时)等)的平均值。模拟过程发现Pc模型无法顺利通过本基准测试，收敛性会随着模拟的进行逐渐变差，经调试时间参数，发现Pc模型只能完成70天左右的基准测试，剩余的部分会由于模型无法收敛而丢失。RH和LPc模型均可完整地通过本基准测试，计算结果均与参考结果十分吻合，但在计算时间上LPc模型占优，仅花费52 s，而RH模型则耗费61 s。

图5和图6示出了两种模型在点A处的模拟结果，前20天的模拟中p>0，室内空气向室外开始渗透，由于室内相对湿度更高(水蒸气分压力较大)的缘故，随着蒸汽扩散向室外扩散，使得该处体积含湿量相应略微增加。但当压差在第21天改变后，室外的空气开始向室内渗透，使得该处的温度快速降低，同时干燥的室外空气使得墙体的含湿量也不断降低，整个过程中，RH模型温度和体积含湿量的计算结果关于参考值的平均偏差为-2.48%和-0.86%，LPc模型温度和体积含湿量的计算结果关于参考值的平均偏差为-0.94%和9.22%。

图5 墙体0.05 m处温度随时间变化的情况Fig.5 Temperature variation with time at the distance of 0.05 m

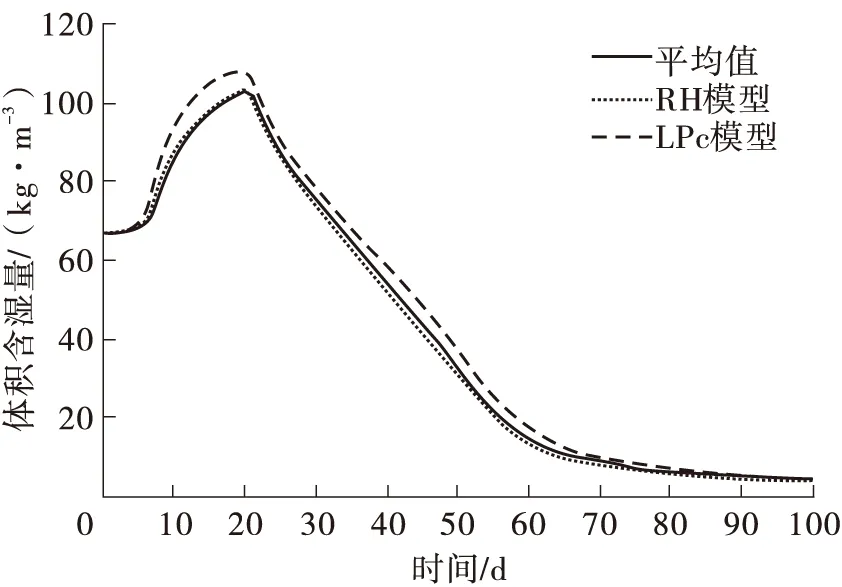
图6 墙体0.05 m处体积含湿量随时间的变化情况Fig.6 Moisture contents variation with time at the distance of 0.05 m

从图7-图8可以看出，在点B处，也由于空气渗透方向的改变使得墙体的热湿分布状况发生了显著地变化。在图7中，仿真开始初期的温度的骤降是由于初始条件中并未考虑墙体内部的初始压力，仿真开始后边界条件引入了30 Pa的压差，并且更加靠近室外低温侧，使得温度出现了骤降；随着室内暖湿空气向外渗透，该处的体积含湿量逐渐上升；在压差改变方向后，可以看出随着室外空气的渗透，该处的温度和体积含湿量也开始不断降低。整个过程中，RH模型温度和体积含湿量的计算结果关于参考值的平均偏差为1.21%和-2.96%，LPc模型温度和体积含湿量的计算结果关于参考值的平均偏差为2.76%和4.32%。

图8 墙体0.19 m处体积含湿量随时间变化的情况Fig.8 Moisture contents variation with time at the distance of 0.19 m

图7 墙体0.19 m处温度随时间变化的情况Fig.7 Temperature variation with time at the distance of 0.19 m

从以上对比可以看出，RH模型在计算本案例时更加准确，但LPc模型也满足精度要求，此外，上述结果也充分证明了空气渗透对于墙体热湿状况的显著影响。

4 实际工况的计算及对比分析

上文基准案例对于新建模型的准确性进行了充分验证，并与RH模型和Pc模型进行了适用性、计算效率方面的对比。但基准案例的墙体两侧边界条件都基本上为静态边界，与室外表面长期暴露在非稳态热湿气候作用下的实际情况有较大出入，和南海岛屿上承受的极端热湿气候更相去甚远；因此，还需使用新建模型对实际工况进行计算并与其他模型进行比对。

本研究将地点选择在南海的典型岛屿永暑礁(北纬9°33′，东经112°53′)，选择西向200 mm厚轻质混凝土墙体作为模拟对象，墙体外表面做淡黄色处理。从建筑节能用典型气象年[20]中选择最热月7月的气象参数作为室外边界条件(包括温度、湿度和太阳辐射)。室内采用空调房间工况，即室内气温26 ℃，相对湿度60%。依据《民用建筑供暖通风与空气调节设计规范》[21]，舒适性空气调节的室内正压值宜取5 Pa，因此，将室内外压差设为5 Pa用以计算空气渗透。内外表面对流换热系数分别为23 W/(m2·K)和8.7 W/(m2·K)，质交换系数为2×10-7kg/(Pa·m2·s)和3×10-8kg/(Pa·m2·s)，外表面太阳辐射吸收系数α=0.5，墙体初始温度为26 ℃，相对湿度为60%(LPc=7.848 8 Pa，pc=7.059 9×107Pa)。上述墙体构造及边界条件参数如图9所示，热湿物性参数见表1。

表1 墙体的物性参数[22]Table 1 Material properties of wall[22]

图9 墙体构造及边界条件参数Fig.9 Configuration of the wall and boundary condition parameters

网格采用较细化划分，需要求解110个自由度(包括4个内部自由度)，相对容差选择1×10-11，模拟时间持续31天。在永暑礁室外极端热湿气候作用下，发现Pc模型收敛性差，计算进程极其缓慢，无法满足实际需要，RH模型和LPc模型均可完成该工况的计算。

如图10(a)和图10(b)所示，受室外高温高湿和强太阳辐射的影响，外表面温度和体积含湿量随时间发生剧烈的变化，但两种模型计算出的结果范围有所不同，LPc模型的外表面温度范围为26.18～41.02 ℃，RH模型的在26.75～40.46 ℃之间，前者比后者大了1.13 ℃；在同一时刻，两者温度计算值最大相差0.86 ℃，整个工况中，平均相差0.29 ℃；LPc模型的体积含湿量变化范围为17.70～57.80 kg/m3，RH模型的为19.66～47.35 kg/m3，LPc模型计算结果的范围比RH模型的大了12.41 kg/m3；同一时刻，两者计算值最大相差21 kg/m3，整个工况中，平均相差4.39 kg/m3。如图11(a)和图11(b)所示，室内表面的温度和含湿量变化均呈现出周期性的波动，但两种模型的计算结果同样有所差异，LPc模型内表面的温度计算结果在25.79～27.70 ℃之间，RH模型在26.05～27.21 ℃之间，前者比后者大了0.75 ℃，同一时刻，两模型温度计算结果最大相差0.58 ℃，平均相差0.19 ℃；LPc模型的体积含湿量计算范围为25.60～31.44 kg/m3，RH模型的为27.21～29.04 kg/m3，前者的范围比后者大4.01 kg/m3；同一时刻两者体积含湿量计算结果最大相差3.14 kg/m3，平均相差0.91 kg/m3。

(a)外表面温度

总体来看，LPc模型的计算结果范围较RH模型大，温度计算值上两模型相差0.86 ℃以内，但在体积含湿量上相差较大。这主要是因为体积含湿量在两模型中均为相对湿度的单值函数，RH模型可直接求解方程得到相对湿度，而LPc模型还需要通过开尔文关系进行一次转换得到相对湿度，使得温度计算的不同被再一次带入到相对湿度计算中，导致体积含湿量计算结果出现较为明显的差别。

(a)内表面温度

在本工况中，两模型耗时与之前截然不同，RH模型耗时378 s，LPc模型耗时601 s。显然，对于长时间动态边界条件的计算工况，RH模型可节约大量的计算时间。但根据已有研究，以相对湿度作为湿驱动势，模型将无法计算存在结露、干燥材料突然受潮等现象的工况，但LPc模型可以应对[3,15]，而上述工况墙体内部并不存在结露。可以推断在考虑空气渗透过程后，对于可能存在上述现象的工况，应当选择LPc模型。

5 结论

针对南海地区极端热湿的气候特征，本研究以毛细压力对数为湿驱动势，考虑空气渗透过程引起的热湿变化，建立墙体内热湿耦合传递模型。采用了HAMSTAD基准测试2、3对新建模型进行验证，并与已有RH模型、Pc模型进行适用性、准确性以及计算效率的对比，最后以南海永暑礁7月的气象数据作为实际工况，使用3种模型进行计算并展开对比，得到了以下结论：

(1)新建模型可通过HAMSTAD基准测试2、3，计算结果精度满足使用要求，可模拟墙体内包含空气渗透的热湿耦合传递；

(2)Pc模型无法完整计算基准测试3，新建模型在基准测试2、3中收敛速度快于其他两种模型，推荐在静态边界条件工况下使用LPc模型；

(3)长期永暑礁实际气象边界条件下，仅LPc模型和RH模型可完成计算，RH模型收敛速度快且结果波动小，推荐在常规工况使用RH模型，在可能存在结露、干燥状态突然受潮等现象的工况下，应当采用LPc模型。