从典型考题中探析圆锥曲线题型破解之策

新疆生产建设兵团第二师华山中学 张庆磊

高中数学教学中，圆锥曲线是重点知识内容，也是数学高考的主要考点，通常是以综合类题型出现在卷面上，并且都是处于压轴题位置，题型变化多端，非常灵活，主要考查学生的数学知识运用能力，也是圆锥曲线题型的典范。因为向量、导数知识相对比较充实，使得圆锥曲线试题朝着丰富形式发展，都是基于数学基础知识层次，考查不同数学知识点的组合，需要学生真正掌握题目内容，懂得数学知识点之间的联系，从而可以更好地整合数学基础知识，提升高考圆锥曲线压轴题解题效率。

一、圆锥曲线经典题型展示

（1）假设直线l 和经过点P 的切线垂直，求线段PQ 中点M 的轨迹方程；

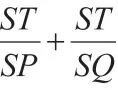
此道高考圆锥曲线题是一道综合题，是由直线、抛物线和不等式等基础数学知识整合起来的一道轨迹方程题，主要考查学生解析几何思想以及综合解题能力。此题解决方式多种，具体解法如下：

（1）假设P 点的坐标是（xa，yb），Q 点坐标为（xc，yd），M点坐标则为（x0，y0），根据题意可知，xa≠0，yb和yd都大于0。

则可以得到y=x2,那么y'=x0①,

所以过点P 的切线斜率则为k切=xa，

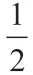
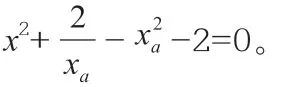
又因为点M（x0，y0）是直线PQ 的中点，

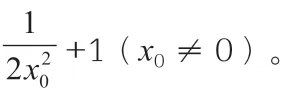
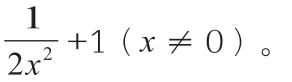
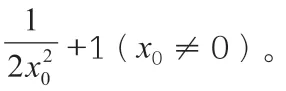
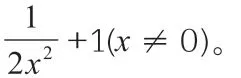
（2）假设直线l：y=kx+b，结合题意可以得到k ≠0，b ≠0，那么T（0，b），过点P 和点Q 分别作PP'垂直于x 轴，QQ'垂直于y 轴，垂足依次是P'，Q'，那么：

消去x 能够得到y2-2(k2+b)+b2=0 ③，

通过方程③可以得到两个相异实根，则Δ=4（k2+b）2-4b2=4k2（k2+b)＞0，于是k2+2b ＞0，那么k2>-2b,

二、解题对策分析

圆锥曲线主要是圆、椭圆、双曲线和抛物线知识的整合，统一定义则是到定点的距离和到定直线之间的距离比是e，点的轨迹则可以称为圆锥曲线，当e ＞1 时为双曲线，当e=1 时为抛物线，e ＜1 则为椭圆。解析几何一般包含两种问题类型，一种是结合题中假设条件，从而可以求出平面曲线表示的方程；一种是借助方程，对平面曲线性质具体分析，进而可以求出一个动点轨迹的方程。借助题目中假设的几何关系，再借助解决数学问题的数形结合思想，转变为寻求变量之间的关系，结合此类数学问题，充分挖掘出数学几何关系，从而可以将复杂问题转化为简单问题。圆锥曲线方程这章节数学知识包含的内容比较丰富，过程比较烦琐，对于学生来说，很多结论无法一一记忆，解决问题的关键在于掌握圆锥曲线的基础知识概念和实质等，通过数学基础知识的掌握，真正解决实际问题，进而可以得到直线和圆锥曲线之间存在的关系，通过此种形式不断提升高中学生数学问题解决能力，从而真正提升高中数学问题解决效率，在高考中获得更高成绩。

总而言之，高中数学知识中，圆锥曲线通常是数学试卷的压轴题，是各种数学知识的整合，针对此数学知识，要具体分析，掌握圆锥曲线的基本概念和性质等，灵活应用，还要通过各种解题形式掌握具体思路，探寻数学解题规律，在日常数学教学中加以训练。唯有这样，学生未来在高考中才能够更好地应对圆锥曲线题目内容，提升问题解决效率，使得学生可以在高考中获得更好分数，促进自身发展。