纵向振动的三角形刀头研究

贺洋洋

(甘肃医学院临床医学系，甘肃平凉 744000)

超声手术刀主要通过超声波振动产生冲击加速度和声微流作用，从而切开生物组织。刀头上的温度并不高，切开后断面光滑，伤口易于愈合[1]。超声手术刀已被广泛应用于各类病变的切除和血管闭合等手术中，尤其腹腔镜手术。与普通手术刀和电刀相比，具有手术精度高、操作简便、手术创伤区域小、无烟雾、出血量少、手术时间短、术后恢复快等优点[2,3]。

超声切割止血刀的发明者Amaral[4]通过更换不同刀头做了切割软组织的对比实验，发现分离钩式的刀头具有最佳的切割和止血的综合效果，并初步阐释了切割止血的机理。Khambay[5]针对超声骨凿的切骨过程进行研究，研究了切骨过程中切割速度、切割力和进给深度等参数对切割效果的影响。但都没有对工作参数变化引起的负载变化及其对换能器工作特性的影响展开研究。索建军[6]等人的研究表明，当手术刀的工作频率为55.5kHz 时，其刀头振动的振幅应不小于41 才能切开生物组织。

尽管国内外学者对超声刀开展诸多研究，但多限于临床应用观察。切割止血刀的机理尤其微观机理仍不明确[7]。对超声刀负载特性的相关研究甚少，尤其是刀头形状改变对超声手术刀特性的影响研究有限。运用变幅杆一维理论已经对尖刀头进行理论分析，得到刀头在横截面较小的情况下一维理论值更接近仿真值，而且刀头尺寸越大相似度越高、频率越低。利用超声刀在振动频率为55.5kHz 时，运用大尺寸夹心超声换能器、四分之一波长指数型变幅杆和楔形变幅杆模型计算出手术刀尺寸，通过有限元Ansys 进行模态分析和谐响应分析，观察是否在作“纯”纵振动，研究其振动特性，为优化手术刀模型奠定基础。

1 理论推导

超声手术刀是由大尺寸夹心式换能器、变幅杆、刀头组成的振动系统，各结构参数设计是振动的关键[8]。在边界面上力和速度是连续的，所以将振动系统作为一个整体来研究。超声手术刀结构如图1，由换能器、变幅杆和刀头组成[9]。

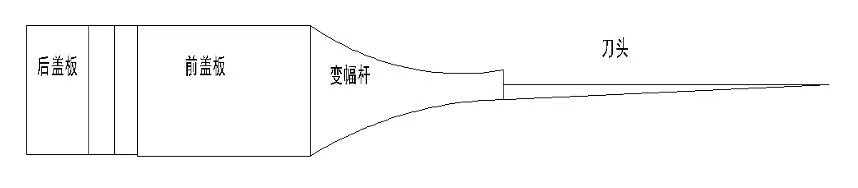
图1 手术刀模型

根据林书玉的推导[10]，四分之一波长振子和四分之一波长聚能器组成一个半波长的换能器，耦合作用下四分之一波长振子的纵向频率方程为：

式中，ρ0为密度，S为横截面积，l0j为四分之一波长振子中压电陶瓷圆片的厚度，kz0j为等效纵振动波数，kz0j=ω/Cz0j，Cz0j为压电陶瓷中的等效纵波声速，Cz0j=(Ez0j/ρ0)1/2。当换能器的振动频率在55kHz时，选用PZT8，性能参数声速c为4560m/s，杨氏模量E取值7.65×1010N/m2，密度ρ=7.5×103kg/m3。超声波传播波长为：

其中c为声速，f为频率，λ1为波长。用l1、l2为前后盖板的长度，压电陶瓷片的直径为D1，压电陶瓷片的厚度为h，压电陶瓷片个数为n，根据张长林等人的研究，压电陶瓷片的直径D1=16mm。四分之一夹心式压电陶瓷换能器前盖板的长度为：

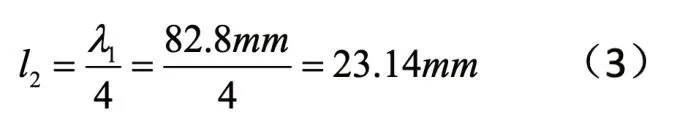
后盖板l1，陶瓷片厚度h=4mm，个数n=2。

采用指数型变幅杆，把超声波的振幅放大至刀具有效加工所需的大小。变幅杆在坐标原点(x=0 处) 的横截面积为S1，(x=l处) 的横截面积为S2。直径分别为D1和D2，长度为l3=λ2/4=1/4×93=23.25mm，放大倍数为N，带负载的指数型变幅杆振动频率方程为：

其中k是为圆波数，l是变幅杆的长度，β=(1/l)InN，ρ为密度。Xl为负载力抗Z02=S2ρc，k'=(k2-β2)1/2。当空载时，Xl=0，k'l=π，当窄端为节点的四分之一波长指数杆时，Xl=∞，(4)式简化为：

其中：E为抗压（拉）弹性常数，c=(E/ρ)1/2，k2=ω2/c2=ω2/E/ρ=ω2×ρ/E=(ρω2/E)l。

三角形手术刀刀头选用45 ＃ 钢，声速c=5192m/s，杨氏模量E=20.27×1010N/m3，密度ρ取值为7.81×103kg/m3，因此：

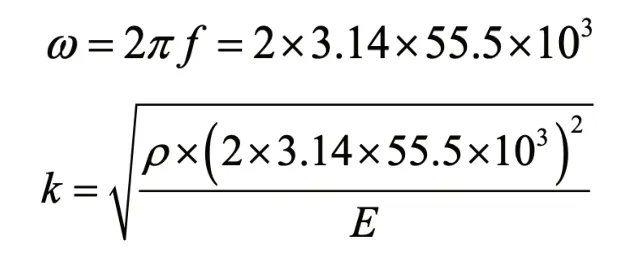
根据参数可得：k=67.67

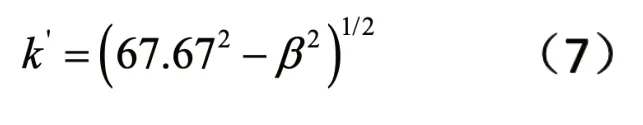
变幅杆放大倍数N=(S1/S2)1/2=R1/R2（8），R1为变幅杆宽端的半径，R2为窄端的半径。

换能器输出位移用ζ1表示，经变幅杆放大后位移为ζ2表示。由于是四分之一波长换能器，ζ1=λ/4=0.0128，ζ2=0.041mm，放大倍数N=ζ2/ζ1=0.041/0.0128=3.2（9），将（9）式代入（8）式，R1=D1/2=8mm，可得：R2=R1/N=8mm/3.2=2.5mm。

用有限元ANSYS 进行模拟时，刀头选择医用钛合金材料TLC4，形状为三角形，密度ρ=4500kg/m3，杨氏模量E=1.1×1011pa，声速c=5077m/s，泊松比σ=0.3。

当刀头横向尺寸远大于纵向尺寸时，可以将三角形刀头等效为楔形变幅杆。

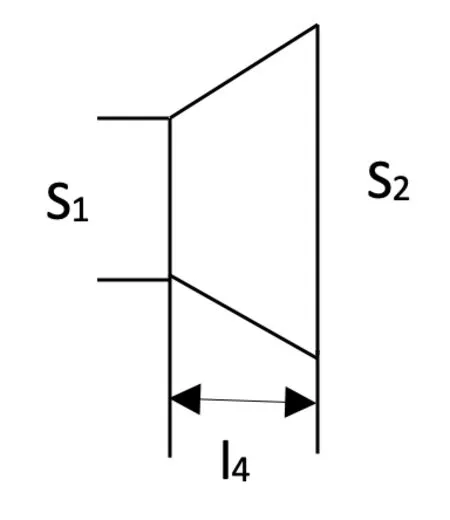
图2 刀头模型

楔形变幅杆等效阻抗为：

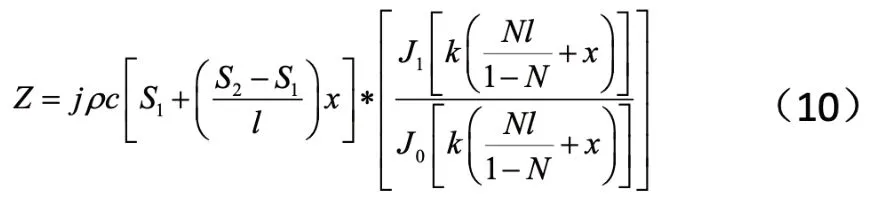
其中：ρ为刀头材料的密度，c为声速，S1、S2为三角形刀头的横截面积，k为圆波数，N为放大倍数，l为刀头的长度，x为节点。当S1=0，(10)式可以变形成：

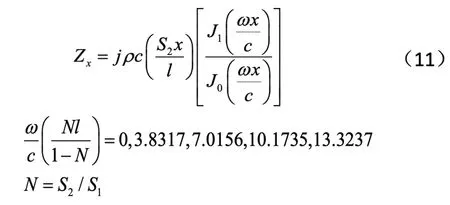
当节点为x0，

当Nl/(1-N)=0 时，其中l为共振长度。节点和最大应力为：

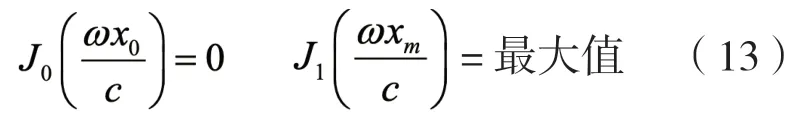
将N=S2/S1代入可得：

当S1=0，ωl/c=3.8317，由钛合金材料参数可得：刀头长度l=3.8317×c/ω=56mm，厚度为d=2mm。

2 有限元建模

2.1 材料属性

超声换能器材料选择，前后盖板为铝；指数型变幅杆选择选用45＃钢；三角形刀头选择医用钛合金材料TLC4。

2.2 单元类型

前后盖板选择PLANE42，压电振子选择PLANE13，指数型变幅杆采用PLANE42，刀头形状为三角形。PLANE13 具有2 维磁、热、电、压电和结构场分析能力，并能在各场之间实现有限的耦合。PLANE13 单元具有大变形和应力刚度能力。在用于纯结构分析时，PLANE13单元也具有大应变的能力。PLANE42 是平面4 节点和平面8 节点单元，8 节点是4 节点的推广，8 节点更精确，对于求解的问题，单元属性可设置平面应力、应变、轴对称等属性。建立模型如图3。

图3 超声手术刀模型

网格划分时，压电换能器采用映射网格划分，变幅杆和刀头采用自由映射划分网格，施加电压载荷，先进行模态分析。

模态分析是其它动力学分析的起点和基础，分析线性结构问题的有限元方程为：

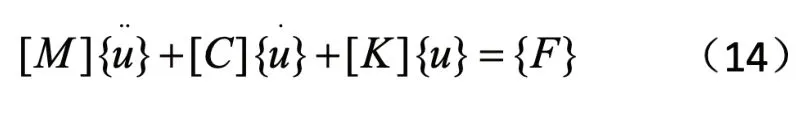
其中[M]、[C]、[K]分别为系统放入质量矩阵、阻尼矩阵和刚度矩阵。{u}、{F}分别为节点的位移向量和载荷向量。当假定ANSYS 结构自由时，有阻尼的情况下，运动方程如下：

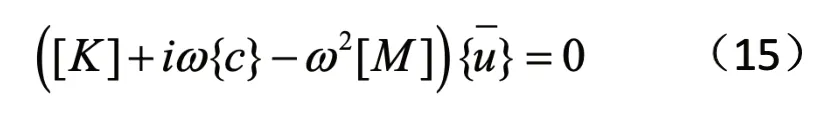
然后进行谐响应分析，谐响应分析采用模态叠加法，振动频率如表1。模拟结果显示，在频率为55.5kHz 的振动为“纯”纵向振动。

3 方法与结果

利用变幅杆一维理论对三角形刀头进行分析，将其作为变幅杆的负载，推出横截面为三角形刀头的振动频率在55.5kHz 时作纵向振动时，换能器和变幅杆的尺寸，并利用有限元Ansys 对刀头进行了模态和谐响应分析，得到当选择换能器长为49mm，直径为16mm，指数型变幅杆的直径为8mm 和5mm，长为24mm，刀头尺寸长为56mm，厚2mm 时，三角形刀头的超声刀才能在频率为55.5kHz 附近作“纯”纵向振动，模拟结果和理论推导结果基本吻合。

表1 ANSYS 模拟三角形刀头手术刀的谐振动频率

4 讨论

李力怡等人利用变幅杆一维理论对尖刀头进行理论分析，将其看成是横截面为楔形的变幅杆，推出基频纵振动频率，并利用有限元对其进行了模态分析，得到刀头在横截面比较小的情况下一维理论值更接近仿真值，而且刀头的尺寸越大相似度越高，频率越低[11,12]。但对于三角形刀头的超声手术刀的振动特性一无所知。对超声刀的诸多研究中，还有一部分是临床应用观察，甚少针对工作参数变化导致的负载变化及其对换能器工作特性的影响展开研究，尤其是刀头形状改变对超声刀特性的影响。采用一维纵振动理论，推导三角形刀头的超声手术刀在55.5kHz 作“纯”纵向振动的换能器、变幅杆、刀头的尺寸。利用有限元Ansys 进行了模态分析和谐响应分析，观察到按推导尺寸建模后，在55.5kHz 的确在作“纯”纵向振动。后期将完善模型，获取“纯”纵振动的振型图、应力、位移分布、导纳特性曲线等参数，系统分析三角形刀头长度、厚度参数对超声振动系统“纯”纵振动的影响，确定综合性能最优的三角形超声刀具，并试制手术刀模型，进行振动模态和位移的实验测量，观察实验数据与仿真结果是否一致。