基于对称残差U型网络的路网交通流量数据修复

代 亮，梅 洋，李曙光，钱 超，汪贵平

(长安大学电子与控制工程学院，西安710064)

0 引 言

智能交通系统依赖于交通数据可用性和准确性进行交通状态和系统性能评估.在交通基础设施快速发展的驱动下，随着交通数据采集设备规模扩大，交通流量数据缺失问题成为智能交通系统领域面临的挑战之一.

交通流量数据修复的核心是从交通数据中发现隐藏的时空相关信息.基于交通数据低秩和时空相关性，文献[1]提出基于低秩矩阵分解的交通流量缺失数据重构方法.文献[2]利用交通网络的时空相关性和道路拓扑信息，提出基于最优闭割的时空数据修复方法.文献[3]提出交通流量时间序列数据多视图学习缺失修复方法，并与长短期记忆网络(LSTM)、支持向量回归及协作过滤算法结合.文献[4]利用卷积神经网络(CNN)对缺失交通流量数据进行编码，重建交通流量数据.文献[5]提出基于生成对抗网络的数据修复方法，将交通量处理为二维信息图，计算路网关联矩阵并实现数据缺失修复.文献[6]将贝叶斯概率矩阵分解模型推广到高阶张量，并应用于交通时空数据修复问题.现有研究存在以下问题：首先，基于时空相关性交通流量数据修复研究多针对较小规模的区域进行[1-2,5-6]，例如只考察路段的直接邻接关系的多个路段(上下游)，较小空间样本的时空交通流信息难以实现大范围路网交通流量数据修复的全局优化，不能有效支持现代交通管控所需的大规模路网交通协同感知与联动控制；其次，将深度学习应用于交通流量数据修复，难以从数据中提取具体时空特征，如基于循环神经网络(RNN)的模型(LSTM等)能为相邻时刻的交通数据建立联系，学习到交通流量序列长期依赖关系[3]，但只能从噪声中捕捉时间特征，不能有效模拟交通路网空间结构.CNN 可通过学习交通路网空间结构进行交通数据修复[4]，但其适合捕捉欧式空间关系，不适用于捕获大规模路网空间特征.

针对能够应用于城市甚至更大空间范围的高精度全域交通数据修复问题，修复模型需要捕捉时空相关性及远距离空间相关性来完成对缺失数据精准重构，且在面对高缺失率情况下能保证数据修复精度.本文提出基于RU-Net 的路网交通数据修复方法，利用模型编码解码能力压缩路网交通数据，减少冗余信息对修复的影响，从而高精度重构缺失数据.模型中残差结构能够提高网络深度，增强模型对原始数据的抽象能力，能捕捉交通数据远距离空间相关性，满足大规模路网中不同缺失率和缺失模式下的交通数据修复场景.

1 模型构造

U-Net的提出是为解决图像分割问题，其模型结构[7]如图1 所示，包含一个收缩路径捕获上下文语义，和一个对称的扩张路径，扩张路径结合收缩路径中各层信息和扩张路径的深层特征输入还原细节信息，模型输入尺寸为572×572 的图像数据，而交通路网中交通信息采集点的数量远小于高分辨率图像像素数量.输入矩阵尺寸较小，仅通过较少次采样，就会出现原始数据细节信息丢失的问题.但简单地直接减少网络深度，会降低模型对输入张量语义信息的编码能力，影响修复的精度.

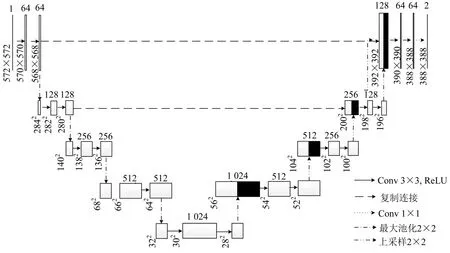
图1 U-Net 结构Fig.1 U-Net architecture

为增加网络深度且不影响网络训练，在U-Net基础上引入残差网络.残差网络(ResNet)利用残差单元模块解决了随网络层次加深带来的优化问题[8].残差单元模块通过将前向神经网络短路连接实现，结构如图2所示，公式为

式中：x和y分别为残差单元的输入和输出；F(x,W)为经过卷积层后的输出结果；W为权重参数.

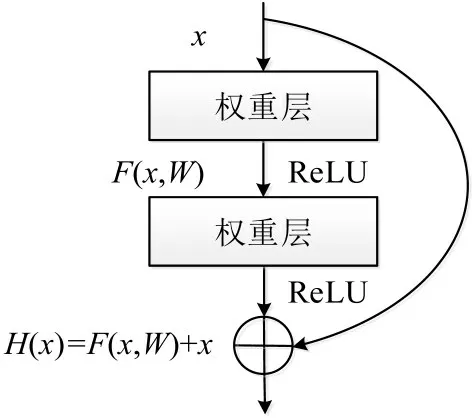
图2 残差单元模块Fig.2 Residual unit

带有短路连接的堆叠非线性层，将输入x通过短路连接传输到输出，只需使非线性层F(x,W)的训练目标逼近0值，便可使残差单元模块学习到恒等映射.加入短路连接后，公式为

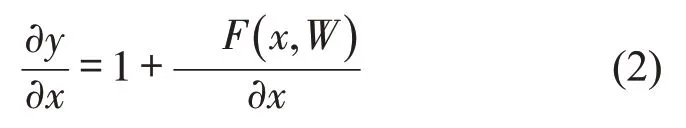
式(2)中H(x)对x的偏导大于1，解决了梯度消失问题.当H(x)为恒等映射时，消除了网络层间仅能逐层传递信息的约束，使信息可以越过多层，解决了随着网络加深而出现的网络退化问题.对于高速公路、隧道及城市快速干道等较封闭的道路场景，可利用交通观测点间远距离空间相关性提高路网交通流量数据修复精度.Moran指数能够反映观测点间的空间自相关性，图3 为伦敦市M3 高速公路中长55 km 路段的18 个交通流观测点Moran 指数在6月1日的变化趋势.从图3 中可以看出，一天中大部分时段Moran 指数小于-0.3，这表明即使观测点间相距较远，仍然具有较强空间相关性.

图3 M3 高速公路Moran 指数日变化趋势Fig.3 Daily trend of Moran Index of M3 freeway

RU-Net 在U-Net 基础上引入残差学习思想，模型结构如图4所示.具体体现在两种短路连接的引入：一种是卷积层之间的短路连接，在增加网络容量的同时，能够解决因卷积层加深出现的网络退化问题；另一种是对称式短路链接，如图4 中收缩路径和扩张路径对称点的黑色短路连接所示，能够在增加模型深度的同时，借助残差单元易于学习到恒等映射的特性，防止因下采样次数较多造成输入交通流量信息丢失问题.通过增加模型对数据的抽象能力，降低数据矩阵压缩率，剔除冗余信息对模型的影响.两种短路连接的作用本质上都是增加模型深度，适应于现实交通场景，加深的网络结构使模型够更容易捕捉到路网交通数据远距离空间相关性.RU-Net 适合处理网格结构数据，将时空交通量矩阵作为模型输入，实验选取路网中1 024 个交通信息采集点，并将5 个历史空间交通量矩阵堆叠至待修复空间交通量矩阵，输入矩阵尺寸为32×32×6，输出矩阵尺寸为32×32×1，即能够一次生成整个路网交通流量数据的修复结果，提高修复效率.

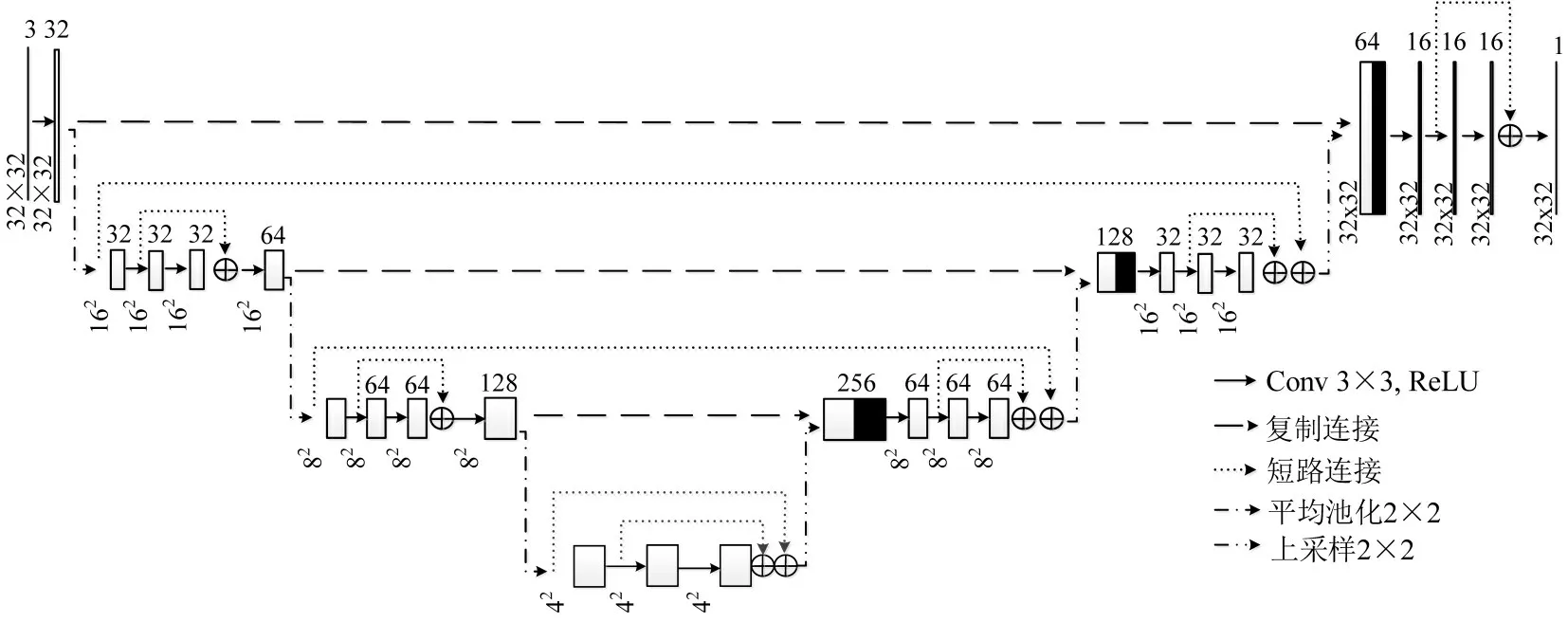
图4 RU-Net 结构Fig.4 RU-Net architecture

2 实验与分析

2.1 实验数据描述

采用英国政府发布的英格兰高速公路交通流数据集[9]对基于RU-Net路网交通流量数据修复方法进行性能验证.如图5 所示，选取伦敦市及周边1 024个交通数据观测点，2013年1月1日～6月30日共181 d的交通量数据，数据采集频率为15 min/次，共17 793 024条记录.其中，80%数据用于训练集，10%用于验证集，剩余数据作为测试集.

图5 伦敦交通数据观测点Fig.5 Traffic data collector in London

2.2 时空交通量矩阵构建

RU-Net 基础结构为卷积网络，是一种专门处理具有网络结构数据的神经网络.为充分捕获路网交通量数据的时间相关性和空间相关性，实验将1 024个交通观测点网格化，根据空间位置顺序构造成32×32的交通量矩阵，共有17 376个空间交通量矩阵，如图6 所示，使模型更易于捕获交通量的空间相关性.图6 分别展示了6月1日08:00 与20:00的路网交通量矩阵，可以看出，路网交通量数据分布相似.图7采用Moran指数分析路网空间相关性：图中区域1为图6(b)中黑色虚线方框范围内共45 个交通流观测点，该区域在早高峰之前路网中交通量空间相关性不显著，随着早高峰来临Moran指数始终低于-0.3且z值均低于-2.58，表明空间相关性较强；区域2 为图6(b)中黑色实线方框，该区域为伦敦希思罗机场，机场周边区域表现出更显著的空间相关性，负相关性表明空间异质特性较为显著.

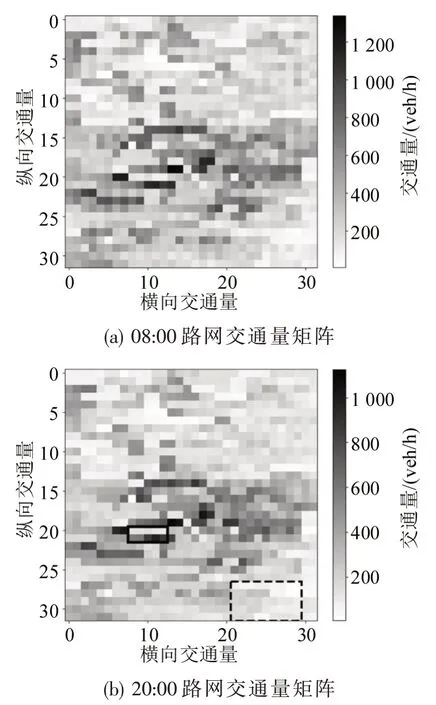
图6 交通量矩阵Fig.6 Traffic volume matrix

图7 Moran 指数日变化趋势Fig.7 Daily trend of Moran Index

由于交通量周期性特点，以周为时间单位选取待修复时间点前两周同时间点交通量矩阵，堆叠至待修复交通量矩阵.为应对交通突发事件，捕获时序交通数据时间相关性，选取待修复时间点的前3个观测间隔交通量矩阵，堆叠至待修复交通量矩阵.6个时间点的交通量矩阵构成32×32×6的时空交通量矩阵，使模型容易捕获交通量时间相关性.

为模拟现实交通环境中路网交通数据的缺失模式，采用3 种空间交通量矩阵生成缺失数据模式.图8(a)为缺失率10%的随机缺失模式，黑点表示缺失数据，在32×32的交通量矩阵中以均匀分布随机采样一定数量观测点作为缺失数据，模拟因为交通数据采集设备故障导致的随机缺失现象；图8(b)为一块10×10 大小的区域缺失模式，在32×32的交通量矩阵中随机位置选取某区域所有观测点作为缺失数据，缺失数据为n×n的交通量子矩阵(0 ＜n＜32)，模拟因区域电力、通讯故障造成的区域数据缺失；图8(c)为混合缺失模式，同时包括前两种缺失模式.此外，为消除随机性影响，实验选取5次实验结果平均值作为最终实验结果.

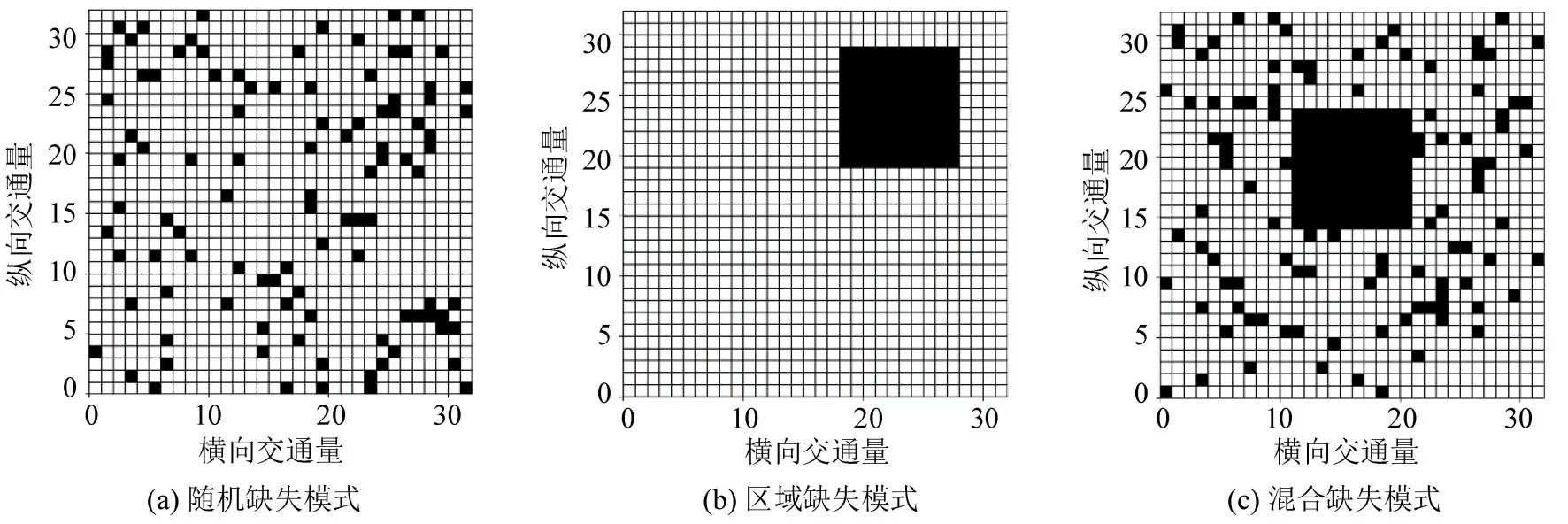
图8 不同缺失模式Fig.8 Different missing patterns

2.3 评价指标

选用均方根误差(RMSE)，平均绝对误差(MAE)，平均绝对百分误差(MAPE)对所提修复算法性能进行评估，表达式分别为

式中：ERMSE为N个交通量观测点的均方根误差；EMAE为N个交通量观测点的平均绝对误差；EMAPE为N个交通量观测点的平均绝对百分误差；i为第N个交通量观测点；xi为交通量缺失数据修复值；yi为交通量数据观测值；N为路网中缺失值数量.

2.4 实验分析

图9 为利用RU-Net 及U-Net 模型对不同缺失率的交通量数据进行修复的结果.从图9 可知：RU-Net 修复结果的RMSE 较低，即使数据完全缺失情况下仅为15.188 8，这表明修复值中极端误差值较小；MAE 及MAPE 评价指标结果表明，RUNet模型修复结果和真实值间偏差小，修复准确率高.在数据缺失率极大的情况下：RU-Net模型仍然具有较强适应性，可以保持较高的修复精度，即使无法从当前空间相关的其他非缺失观测点中获取修复信息，仍能凭借历史交通量数据的时空相关性对数据进行修复；U-Net模型在数据缺失率超过80%后，出现修复精度大幅下降的问题.对比各评价指标可知，RU-Net 模型修复结果均优于U-Net模型，说明RU-Net 模型对数据特征的提取，时空相关性的抽象能力较好，对于缺失数据修复具有较高的精度.

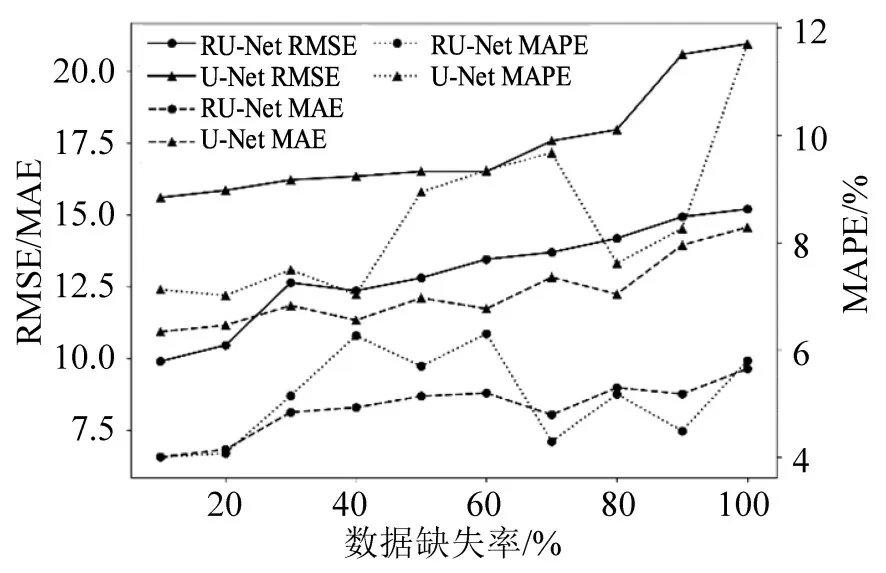
图9 各评价指标缺失数据修复效果对比Fig.9 Imputation effect comparison with different criterions

图10为6月27～28日编号LM1010路段在数据完全缺失情况下的交通量数据修复结果.图10(a)实线椭圆处，当交通流量出现急剧变化时，交通流量随机性加强，修复值易产生较大波动，出现修复精度下降问题，但RU-Net 模型仍能较准确地对数据进行修复；图10(a)中虚线椭圆处，当交通量处于高峰期间，RU-Net模型也能够准确描述数据分布，具有更低的修复误差.

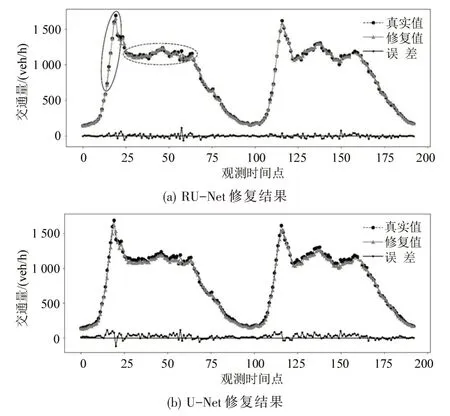
图10 基于RU-Net 和U-Net 模型数据修复性能对比图Fig.10 Performance comparison of data imputation between RU-Net and U-Net

图11 为RU-Net 对不同数据缺失模式修复性能对比.区域缺失模式中，除缺失区域较小时，均方根误差均较相近，表明缺失区域较大时，观测点能找到高空间相关性的非故障观测点较少，更趋向于从历史数据中学习时空映射关系作为修复依据.在相同数据缺失个数条件下，对比随机数据缺失模式修复结果发现，随机缺失模式较区域缺失模式有更高的修复精度.这是因为随机缺失模式中的故障点更容易找到具有高空间相关性的非故障观测点，并利用其数据对故障点进行修复.混合缺失模式中接近1/2 采集点为区域缺失，剩余为随机缺失，随区域缺失采集点数量增多，混合缺失模式的修复误差接近于区域缺失模式.图12 为RU-Net 对100 个缺失采集点修复值MAE 的分布，区域缺失模式中上下边界相差较大，缺失区域中心部分较少依赖于空间域上下文信息，造成修复误差波动较大.实验结果表明，RU-Net 对区域数据缺失模式同样具有较高的修复精度，但区域数据缺失模式中，模型修复更依赖于交通流量的时间相关性.

图11 RU-Net 不同数据缺失模式修复效果对比Fig.11 Imputation effect comparison of RU-Net with different data missing pattern

图12 100 个缺失点修复值MAE 分布Fig.12 Distribution of mean absolute error for imputation

3 结 论

现代化交通系统中管理与决策依赖全域数据支持，路网中出现大面积数据缺失时，无法提供动态实时的路网交通数据.本文将交通流量构造为时空交通流量矩阵，使模型更易于捕捉交通流量的时空相关性；引入残差网络，增强RU-Net 对交通流量数据的适应性.在避免网络退化的同时提高网络深度，增强修复模型对高级语义信息的编码能力，提高模型对远距离空间相关性的捕捉能力，进一步提高修复精度.本文模型在面对交通数据不同缺失率和不同缺失模式时能够得到较高精度修复值，修复结果可应用于交通路网区域联动控制与管理中.下一步研究将考虑复杂多样的交通环境对数据修复的影响，将天气数据、道路及环境条件等量化并融入模型，进一步提升修复模型性能.