换能器布阵型式对超声清洗效果影响的研究*

□ 胡 涛 □ 傅 波 □ 魏周玲 □ 晋 毅 □ 戴素红

1.四川大学 机械工程学院 成都 610065 2.北京泰拓精密清洗设备有限公司 北京 101102

1 研究背景

随着工业化及高新科技产业的持续发展,清洗技术对产品性能、质量、使用寿命、可靠性等方面的影响日益突出,并直接制约生产水平的提高。近年来,绿色环保的新型清洗技术——超声清洗倍受关注,超声清洗机理被不断细化,大功率换能器的设计得到完善,对工件清洗效果产生影响的因素被一一发掘,并被深入研究[1-4]。面对越来越多的市场需求,超声清洗设备开始向大型、高效、环保、精密、自动化等方向发展,应用领域日益扩大。在电子制造行业中,清洗网板上的锡膏和红胶就是超声清洗设备的典型应用之一。

目前,国内电子制造行业还普遍采用气动清洗的方法对网板进行清洗。若采用超声清洗设备,则大多存在设计陈旧、缺乏理论和试验依据、清洗噪声大、清洁度低等缺陷。深化超声清洗理论,利用计算机技术进行数值模拟,结合试验验证设计,优化超声清洗设备是当务之急。

在超声清洗工件的过程中,夹心式压电换能器的声波辐射面积较小,并且声阻抗与清洗液体的声阻抗耦合性较差,甚至存在匹配失调的严重情况。对此,在超声清洗设备中通常将若干个同频率的换能器按一定型式排布粘接于清洗槽底部或侧面,以组成超声振动系统[5-7]。通过同一电信号激励各换能器,共同推动清洗槽面板做简谐振动,向清洗液中辐射声波,从而实现对工件的清洗。在实际生产过程中发现,超声清洗设备中换能器的布阵型式不同,超声清洗的效果也不同。为确定最佳的换能器布阵型式,获得最佳的清洗效果,笔者对三角形、矩形、正方形三种换能器布阵型式进行研究,为超声清洗设备中换能器布阵型式的选择提供参考。

2 有限元分析

在超声清洗系统中,换能器的布阵型式主要有三角形、矩形、正方形三种。换能器的频率和布阵型式不同,超声清洗槽底板声源的振动特性也不相同[8]。采用ANSYS Workbench有限元分析软件,对40 kHz夹心式压电换能器三种布阵型式在清洗槽底板上的振动特性进行分析,比较同频率下不同换能器布阵型式对超声清洗槽板声源振动分布的影响,从而得到相对合理的换能器布阵型式。

笔者采用18个40 kHz喇叭形夹心式压电换能器粘接于超声清洗槽底板,组成超声振动系统。为方便分析,将超声清洗槽底板简化为一块矩形薄板,几何尺寸为520 mm×295 mm×2 mm,四周采用固定支撑,在换能器的激励下做简谐振动。超声清洗槽底板和换能器的材料属性见表1。利用SolidWorks软件建立三维模型,将三维模型导入ANSYS Workbench有限元分析软件,选择谐响应分析模块,添加材料的参数信息。将换能器简化为一个质量块,换能器与清洗槽底板之间采用默认的固定连接方式[9]。使用网格划分工具对模型自动划分网格,设置网格尺寸为10 mm。设置频率扫描范围为39.5 kHz～40.5 kHz,求解步数为10,步长为100 Hz。在换能器表面施加一个Z方向的振动位移载荷,大小为2×10-6m,相位角为零。

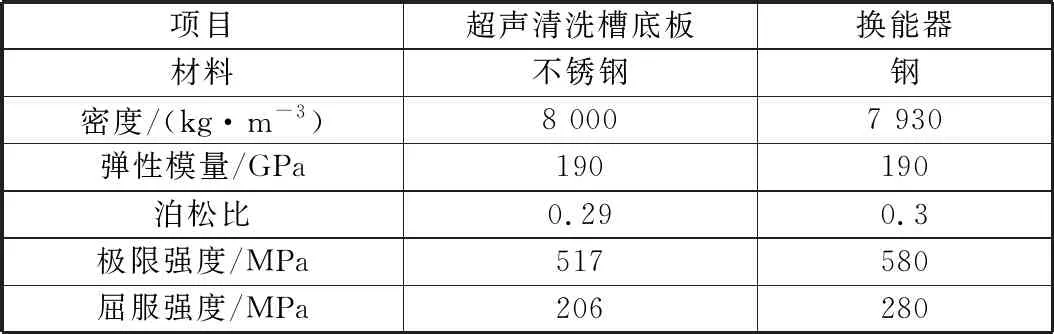
表1 材料属性

换能器三角形布阵型式如图1所示,矩形布阵型式如图2所示,正方形布阵型式如图3所示。设置完成后进行求解,得到40 kHz频率下换能器三角形布阵型式板声源振幅分布如图4所示,矩形布阵型式板声源振幅分布如图5所示,正方形布阵型式板声源振幅分布如图6所示。

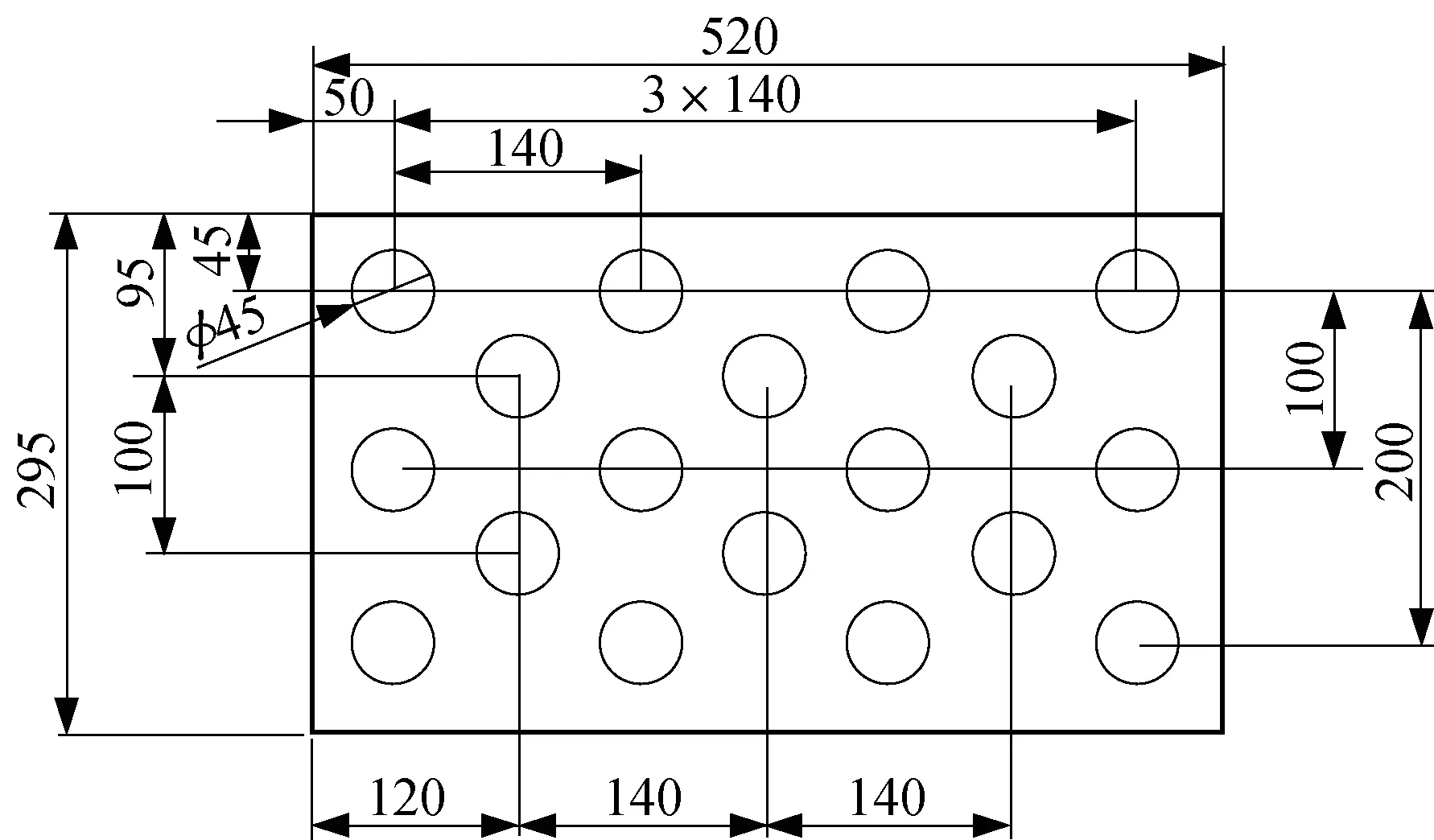
▲图1 换能器三角形布阵型式

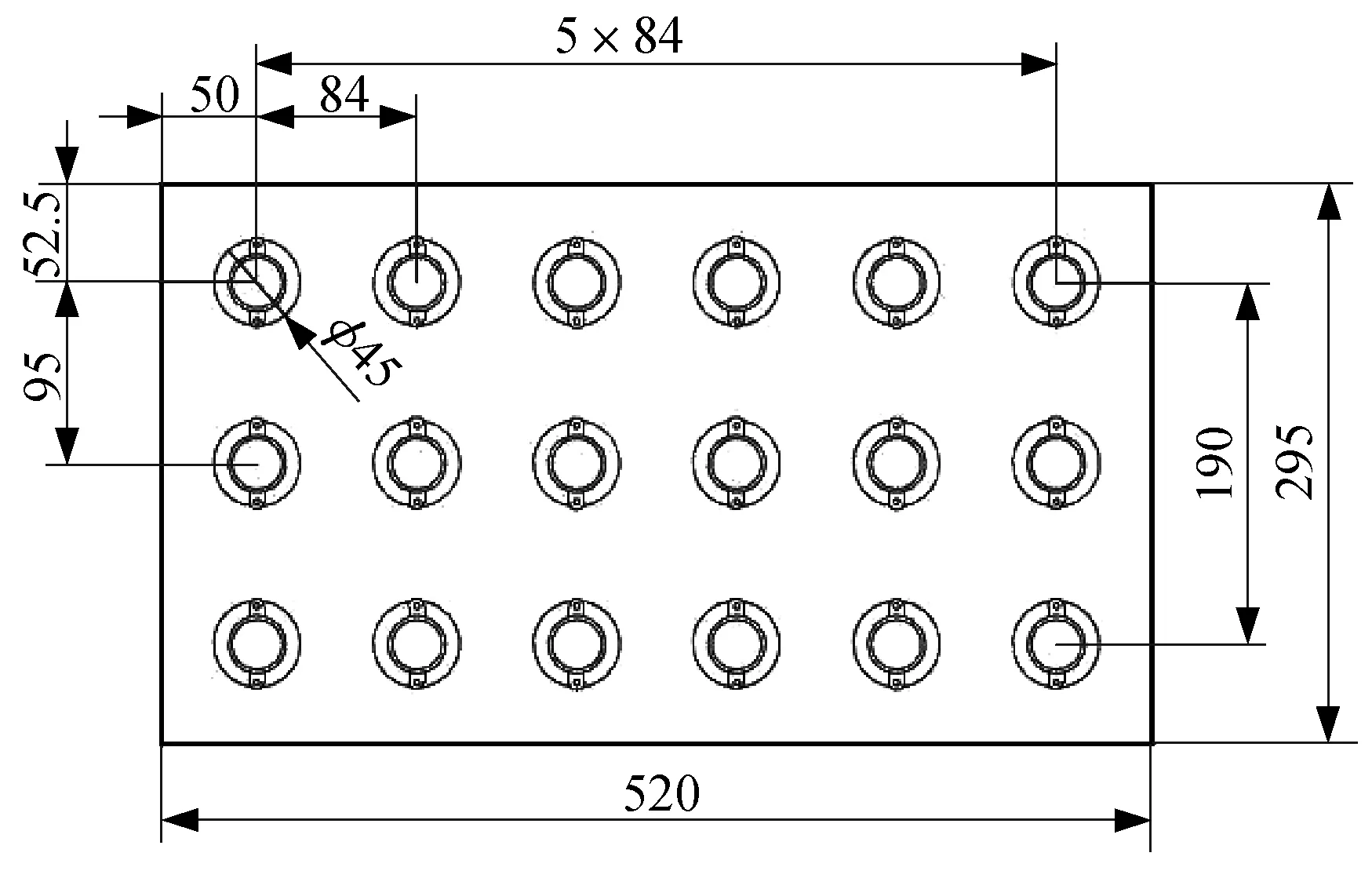
▲图2 换能器矩形布阵型式

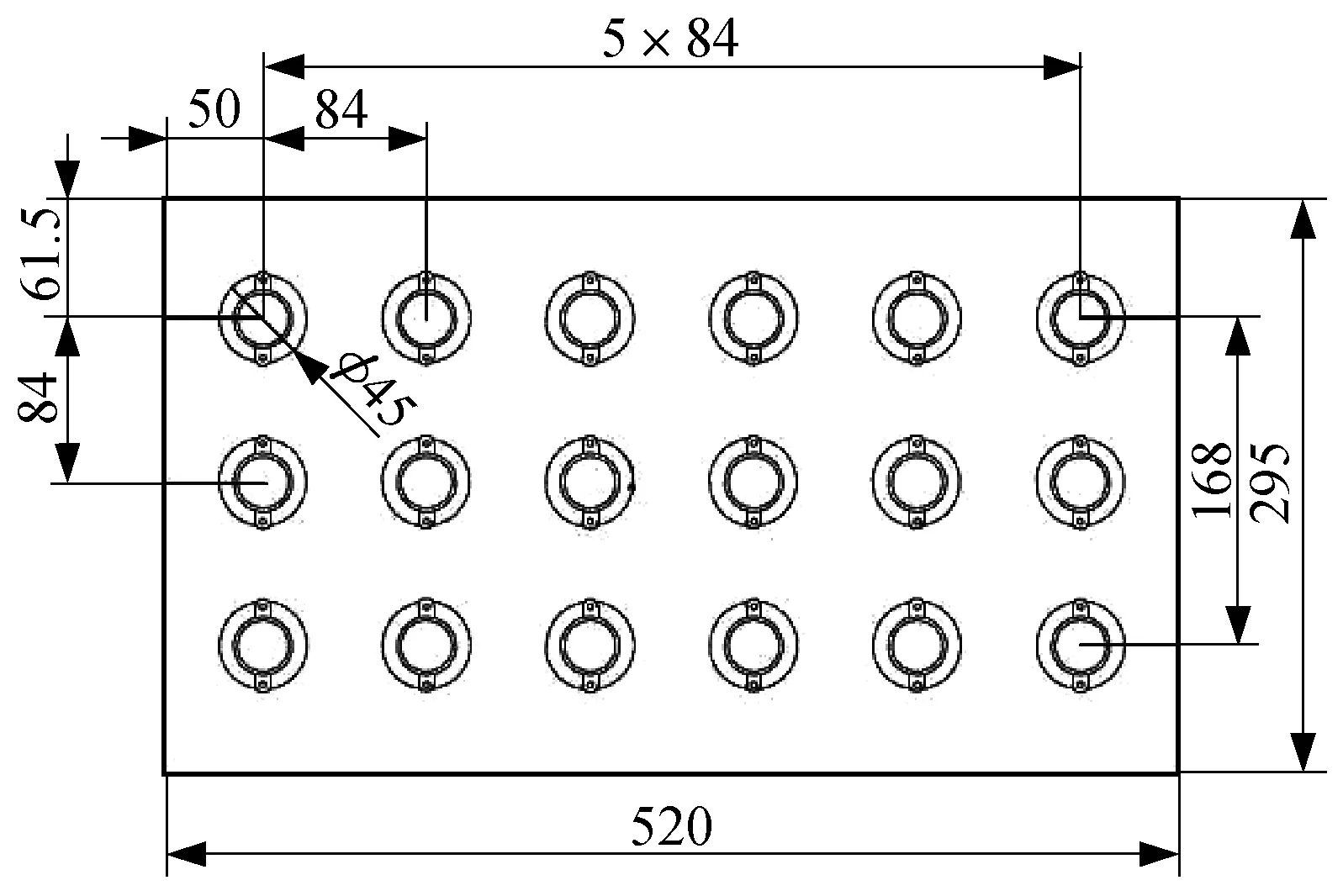
▲图3 换能器正方形布阵型式

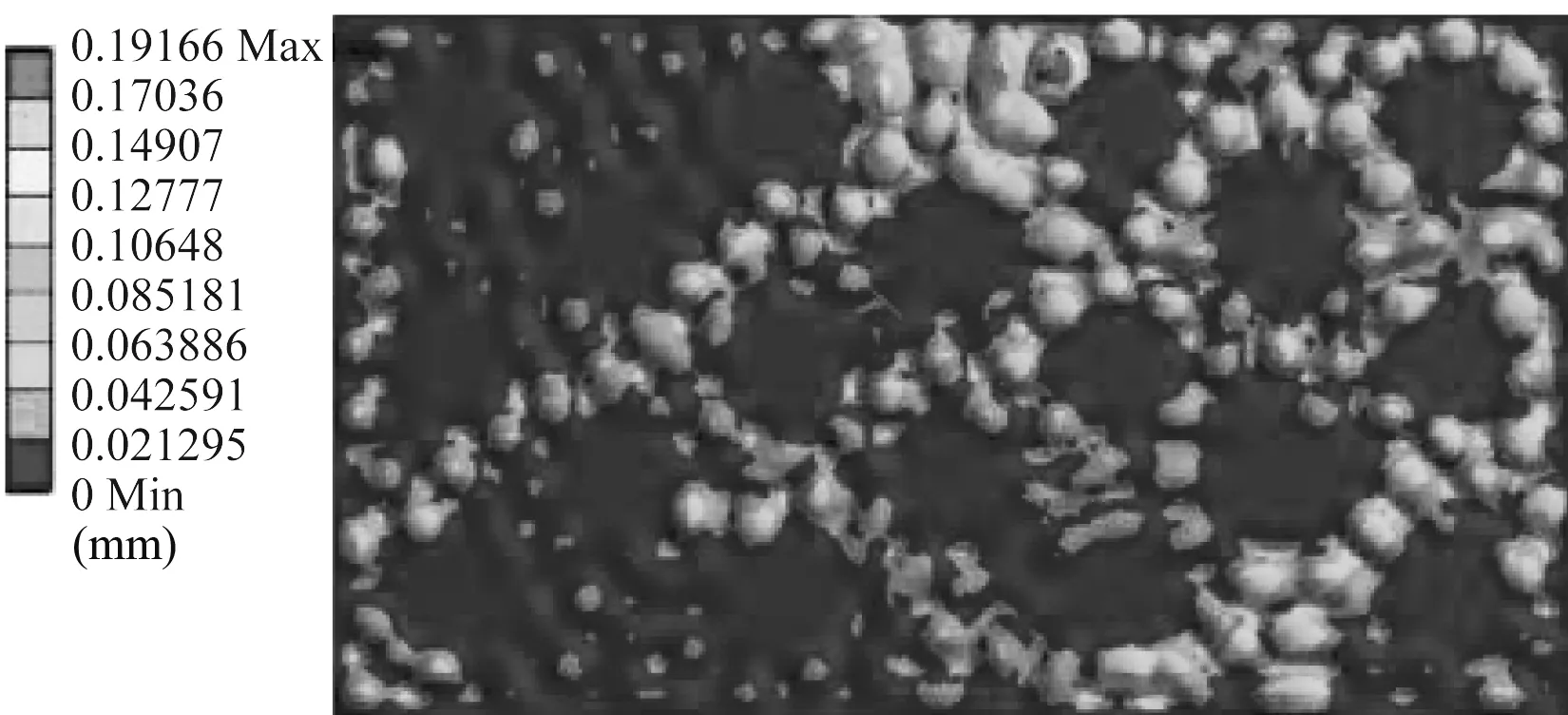
▲图4 换能器三角形布阵型式板声源振幅分布

▲图5 换能器矩形布阵型式板声源振幅分布

▲图6 换能器正方形布阵型式板声源振幅分布

在40 kHz频率下,换能器采用三角形布阵型式时,板声源的振幅明显大于矩形布阵型式和正方形布阵型式,并且板声源振幅分布比较均匀,极值出现较少,可以减小不均匀纵振引起的清洗槽底板弯曲变形,避免造成应力集中,不会形成腐蚀点。由此确定换能器宜采用三角形布阵型式。

3 声场分布数值分析

超声清洗的主要原理是超声空化效应[10],超声振动辐射至清洗液中所产生的空化核处声压大小直接关系到超声空化效应的优劣。因此,声场在清洗槽中应尽可能分布均匀,这样才能够保证清洗效果。

为验证换能器三角形布阵型式的清洗可行性,进行声场分布数值分析。分析时进行如下简化:不考虑声强、功率、温度等因素对声场分布的影响,假设清洗过程只存在超声空化作用[11];将清洗液看作不可压缩流体,忽略黏度及表面张力;忽略清洗槽各面及液面对声波的反射、散射等作用,不计流体边界处的阻尼损耗。将清洗液内的声传播看作理想传播过程,重点分析清洗液静止状态下的声场分布[12]。为方便计算分析,以换能器和清洗槽的粘接面为XY平面,以超声辐射的方向为Z轴,以板声源的对称中心为坐标原点,建立坐标系。超声清洗槽为长方体形状,尺寸为520 mm×295 mm×200 mm,可得简化及变形后的清洗槽内超声波动方程为[13]:

p=AxAyAzei(ωt-kr)pm/r

(1)

(2)

(3)

(4)

(5)

式中:p为声压;(X0,Y0)为换能器辐射面在坐标系中的坐标;pm为换能器输出的声压幅值;Lx、Ly、Lz为清洗槽的形状尺寸;(x,y,z)为清洗槽内空间位置点坐标;r为点(x,y,z)到换能器辐射点的距离;Ax、Ay、Az为声压系数,表征各方向声压分布形式;Nx、Ny、Nz为各方向波的阶次;t为时间;ω为角频率;k为波数;ei(ωt-kr)为声压值在时间t的相位角。

忽略声压随时间的变化,以cos(-kr)表征相位角对声压幅值的影响,并将Nx、Ny、Nz均设为1,且不考虑换能器输出的声压幅值pm,设声压幅值pm为1。清洗液为室温状态下的纯净水,水中声传播速度为1 480 m/s,液体质点流动速度为零。单个换能器以点声源的形式向清洗槽内辐射声波,换能器的谐振频率为40 kHz。

p(x,y,z)=∑AxAyAz[cos(-kr)]/r

(6)

结合式(6),使用MATLAB软件编写程序,对清洗槽内声压分布进行数值计算,清洗液静止状态下超声清洗槽内声场分布如图7所示。

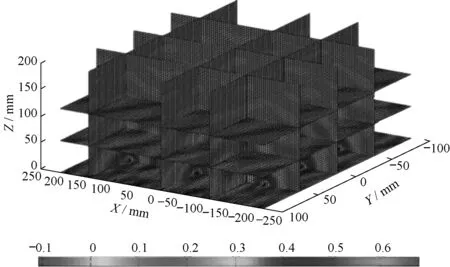
▲图7 清洗液静止状态下超声清洗槽内声场分布

由图7可以看出,在X轴、Y轴方向近声源处声压较大,并且在换能器周围达到最大值,各个换能器周围声压强度基本一致。在0≤Z≤100 mm区域,声压值较大,可以满足清洗要求,并且声压分布较为均匀。在Z>100 mm区域,各面声压的最大值沿Z轴正方向大幅减小,声场分布不均匀。在两个换能器的过渡间隙存在一个声压值几乎为零的区域,为清洗盲区,在清洗时应尽量避免将工件置于清洗盲区。为保证良好的清洗效果,应使工件尽可能靠近超声辐射面位置,并位于XY平面声压较大值处。通过声场分布数值分析,确认换能器三角形布阵型式在清洗液静止状态下可以完成清洗工作。

4 超声网板清洗试验

为进一步验证换能器三角形布阵型式的超声清洗效果,笔者利用现有设备搭建浸泡式超声网板清洗试验平台进行试验。超声清洗时清洗对象为固结于网板上的锡膏,清洗液温度为40 ℃,时间为8 min,功率为1 500 W。采用热风烘干时,时间为8 min。

试验完成后使用手持式显微镜观察网板表面洁净度,如图8、图9所示。网板表面及微细漏孔边缘无污物残留,清洗洁净度符合要求。由此可见,在超声功率为1 500 W时,采用换能器三角形布阵型式,对固结于网板上的锡膏超声清洗8 min,便可以达到预期的清洗效果。

▲图8 超声网板清洗试验网板洁净度

▲图9 超声网板清洗试验网板局部放大洁净度

5 结束语

笔者结合声学理论,通过有限元分析、数值分析及试验,证明了换能器的布阵型式会影响清洗槽底板表面的声辐射分布,从而影响超声清洗效果。换能器采用三角形布阵型式,相比矩形和正方形布阵型式,振幅更大,振动更均匀,能够达到预期的清洗效果。在超声清洗设备中,建议优先选用三角形布阵型式换能器。