城际动车组车轮I类滚动接触疲劳机理研究

(西南交通大学牵引动力国家重点实验室，四川成都，610031)

为最大程度上方便乘客和保证客运量，城际动车组往往具有站间距短、加减速频繁的特点[1-2]，且线路小半径曲线常常难以避免。这些使得城际动车组车轮服役环境甚至较高速铁路更恶劣。近年来，我国某城际线路上运行的200 km/h 速度级城际动车组在运营过程中发生了很多如图1所示的车轮连续型滚动接触疲劳，如果任其发展，其中的疲劳裂纹会在晚期导致表面材料剥离，引发振动和破坏运行平稳性的同时，辐射轮轨噪声，降低列车舒适性，甚至威胁行车安全[3-4]。因此，日常管理中动车所会及时镟修疲劳车轮，恢复其接触表面，这又不可避免地缩短车轮服役寿命，增加运营成本[5-6]。

图1 我国某城际动车组车轮发生的I类滚动接触疲劳Fig.1 RCF class I occurred on wheels of intercity EMUs in China

根据DEUCE[7]对车轮连续型滚动接触疲劳的分类，图1所示的疲劳裂纹属于典型的I 类滚动接触疲劳(处于名义滚动圆外侧)。王玉光等[8]研究了250 km/h动车组车轮上发生的I类裂纹，发现其处于名义滚动圆外侧15～30 mm 内，在镟后里程(10～15)万km开始出现，很少发展至剥离掉块阶段，其根本原因是曲线段低轨侧轮轨廓形匹配不合理。陶功权等[9-10]研究了120 km/h 的普铁客车车轮上I类疲劳和所导致的剥离，确认其主要原因为曲线通过区段上磨耗轮轨匹配不佳。HOSSEIN 等[11]建立了车辆动力学模型，基于损伤函数滚动接触疲劳模型，利用遗传算法优化了一种车轮廓形，缓解了北欧重载铁路机车车轮的I 类疲劳。采用车辆-轨道耦合动力学和损伤函数模型，温邦[12]发现某地铁车轮的II类疲劳(处于轮缘根部)的萌生原因是车辆通过小半径曲线时非导向轴高轨侧车轮与钢轨间相互作用，并提出使用轮缘润滑器和适当增加扣件横向刚度的减缓措施。针对大功率机车车轮发生的III类疲劳(处于名义滚动圆附近)，LIU等[13]开展了现场调查和模拟分析，发现小半径曲线、长大坡道等复杂环境为其主要原因。

人们对滚动接触疲劳的机理和影响因素进行了研究。黄育斌等[14]通过实验发现，车轮所受的垂向力、横向力和冲角越大，车轮表面疲劳裂纹越容易萌生扩展。基于实验结果，MAGEL 等[15-16]发现第三介质液体会加速已萌生滚动接触疲劳裂纹的扩展，但在裂纹萌生之前，液体会因润滑作用而降低轮轨间应力水平，减缓疲劳裂纹的萌生。CHEN等[17]研究了不同制动条件下车轮的滚动接触疲劳行为，发现制动力和制动时间的增长会加剧疲劳裂纹萌生。赵相吉等[18]指出车轮表面硌伤会减小滚动接触疲劳萌生寿命。吴娜等[19-20]发现轮轨廓形对轮轨接触点的位置及蠕滑力等有决定性影响，从而直接影响车轮滚动接触疲劳裂纹的萌生和扩展。

本文作者针对图1中200 km/h速度级城际动车组车轮I类滚动接触疲劳现象进行研究，具体包括基于现场观测数据的统计分析和基于车辆系统动力学分析的滚动接触疲劳预测。在此基础上，揭示该城际动车组I类疲劳裂纹的发生机理，找出其关键影响因素，并提出相应的治理措施。

1 现场观测数据统计分析

首批4 列200 km/h 速度级城际动车组于2017年4月上线，第二批12 列在2017年12月上线，2018年以后，保持16 列动车组的规模。2018年4月之前，所有动车组不调头往返运行，动车组在线路上的方位与朝向如图2所示，即由北向南运行(A站→B站)时1车1轴导向，返程时8车4轴导向。另外，以面向1 车的站位来定义列车左右侧(L 和R)，以南向北运行定义左右曲线，如图2所示。依此定义，列车通过左曲线时左侧车轮在低轨侧。从2018年4月起，所有动车组每3月调头1次，以避免偏向一侧的车轮损伤。

图2 城际线路上动车组方位(调头运行前)Fig.2 Orientation of EMUs on intercity line(before turning around)

1.1 车轮滚动接触疲劳调研

就上述车轮滚动接触疲劳问题进行4次车轮普查(分别在2017年7月、9月、12月和2019年1月开展)，前3次普查均涉及4列动车组，在其第1个镟修周期内(首次全列镟修前，总里程小于23万km)，第4次普查涉及12列动车组。图3所示为车轮疲劳裂纹种类、个数及占总车轮比例。从图3可见：动车组车轮第1 次和第2 次普查时萌生了I 类滚动接触疲劳，2 次普查的发生率(疲劳轮数与调研总轮数之比)分别为4.59%和25.40%。期间，动车所安排对部分损伤较严重的车轮进行了单独镟修。第3次普查时仅存在II 类滚动接触疲劳，发生率为7.03%；第3 次普查之后，动车所对首批的4 列动车组进行了全列车轮镟修；第4 次普查时，I 类和II 类裂纹均存在，但总发生率仅为5.47%，且以I类裂纹为主，部分车轮上两者共存。

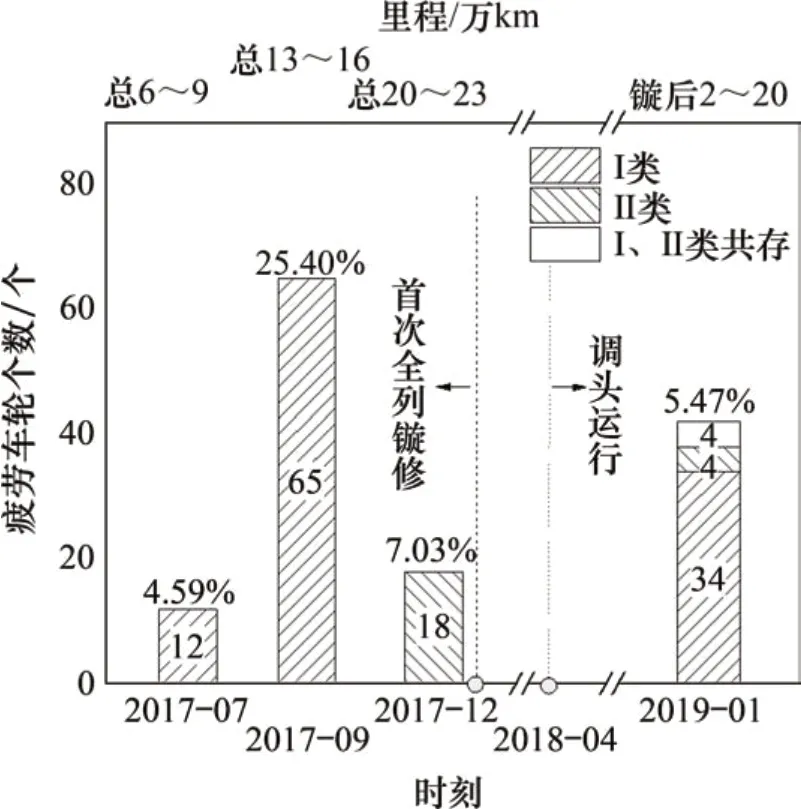
图3 车轮疲劳裂纹种类、个数及占总车轮比例Fig.3 Class,number and proportion of fatigued wheels

图4所示为车轮疲劳裂纹演化过程。图4(a)中横坐标零点定义在踏面名义滚动圆处，向踏面外侧定义为横坐标正向。从图4可见：第1次普查时的I类疲劳集中在名义滚动圆外侧5～15 mm的范围内，第2 次普查时稍稍扩展至5～20 mm，第3 次普查时发生的II 类疲劳集中在-30～-10 mm 的范围内，第4 次普查时I 类疲劳发生区域比前3 次的更靠近踏面外侧，但II类疲劳区域基本上与第2次的重叠。根据图4(b)前3次普查时表面连续裂纹视觉上清晰，I类裂纹存在细小剥离，但定期调头运行后的第4次普查中，虽然I类和II类疲劳均有发生，但严重程度较之前明显减轻，未见可辨识的剥离，尤其是发生率更高的I类疲劳。

图5所示为历次普查中发现的疲劳车轮的轮位分布。其中头尾车是指1车或8车，导向轴对专指整列动车组的导向轴对，即1 车1 轴和8 车4 轴，对应着往返运行。从图5可知：第1次普查中发现的疲劳车轮全部发生在头尾车的左侧车轮上，且66.70%发生在导向轴对上；第2 次和第3 次普查中，在头尾车和导向轴对上的集中度显著下降，但依然集中在左侧车轮上；定期调头运行的第4次普查中，发生在左侧车轮的概率进一步降为54.80%，即两侧发生概率接近相同。

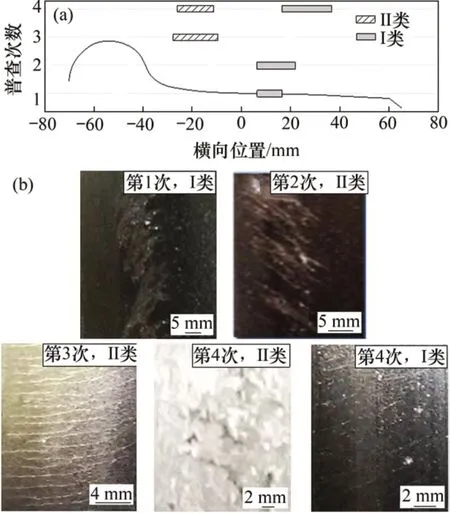
图4 车轮疲劳裂纹演化过程Fig.4 Evolution of zone and appearance of fatigued wheels

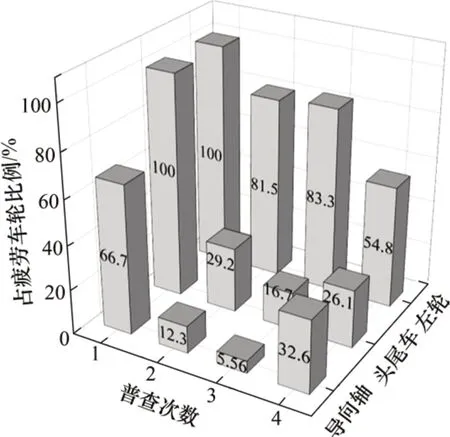
图5 疲劳车轮的轮位分布Fig.5 Position distribution of fatigued wheels

作为对比分析，调查另外2个城市的同型城际动车组2 和8 列，共10 列，均发现了I 类和II 类疲劳，相应发生率分别为1.88%和1.56%，疲劳程度都非常小(与图4中第4 次普查的踏面类似)，也未见偏向一侧或集中在头尾车或导向轴的现象。

综上所述，该城际动车组车轮可发生I和II类疲劳。I类疲劳发生概率更大，也更易发生，其严重程度比II 类疲劳的高，在运行中导致车轮镟修。所以，以下分析着重针对I类疲劳展开。

1.2 轮轨廓形测量

从第4次普查开始，本文作者选择2列动车组进行跟踪测试，测量车轮廓形随里程的演化，为模拟提供基础数据。另外，针对上述城际线路测量4 个曲线段上的钢轨廓形，其半径分别为350，450，400和1 200 m。

2018年5月，在现场测量14 列动车组的车轮廓形(由于当时未记录车轮表面状态，故未列入普查之中)。图6(a)所示为当时某动车组某轴左右两侧车轮的实测廓形，定义名义滚动圆位置坐标为0。从图6(a)可以看出：右轮轮缘磨耗明显比左轮的高，即存在轮缘偏磨。所测量14 列动车组左右两侧的平均轮缘磨耗量与镟后里程之关系如图6(b)所示。图6(b)中，同一列车的结果被框在一起，实线框对应着图6(a)所示动车组。因为在2018年5月，动车组刚开始定期调头运行1月(运行里程大约为3 万km)，所以，其影响应该还未充分显现，可在分析中予以忽略。从图6(b)可见：未调头时，轮缘偏磨量大致随着镟后历程的增大而增加。定期调头约1 a 的2019年1月，偏磨现象明显减轻，见图6(c)。

1.3 运行线路曲线调查

如前所述，定期调头前，发生了偏向右侧车轮的轮缘偏磨，而滚动接触疲劳集中发生在左侧车轮。考虑到轮缘磨耗和车轮I类和II类疲劳均与车辆曲线通过行为紧密联系，所以，有必要就上述动车组所运行线路的曲线情况进行调研。

上述城际线路全长117 km，其中曲线全长63.2 km。图7所示为不同半径范围内左、右曲线长度统计。从图7可见：半径350～450 m的小半径曲线全为左曲线，总长1.4 km(占全线路曲线长度的2.21%)，而800～1 600 m 中半径曲线全为右曲线，占比4.11%。另外，不同半径曲线上的轨底坡实测结果也存在很大波动，如表1所示。

2 数值模型

2.1 车辆多体动力学模型

图6 动车组车轮轮缘磨耗统计Fig.6 Wheel profile flange wear statistics of EMUs

因为上述车轮滚动接触疲劳以头尾车(拖车)的疲劳损伤最严重，故下文的数值分析中仅考虑单节拖车建模。此外，所分析的滚动接触疲劳沿车轮1周连续出现，故其与轮轨间准稳态相互作用相关，而与高频动力作用无关。为突出低频动力作用和降低计算量，使用多体动力学软件SIMPACK建立车辆系统动力学模型作为滚动接触疲劳预测的基础，见图8。轨道仅由2 条刚性钢轨表征，施加武广轨道谱来模拟轨道不平顺。主要车辆参数见表2。

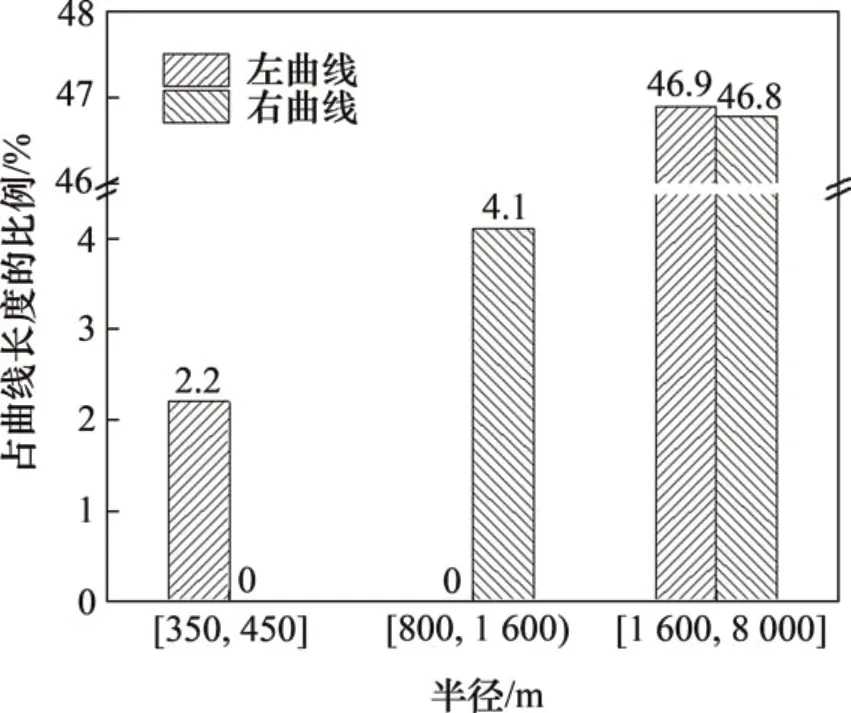
图7 上述城际线路上不同半径范围内的左、右曲线比例Fig.7 Proportion of left and right curves within different radius on the above intercity line

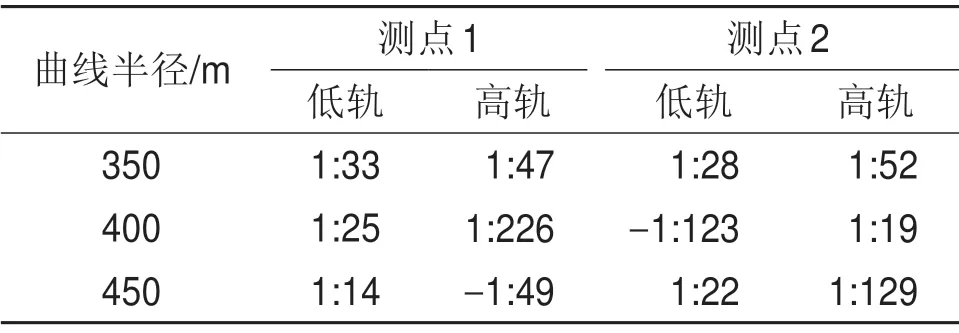
表1 不同半径曲线上的轨底坡实测值Table1 Measured values of rail bottom slope on different radius curve

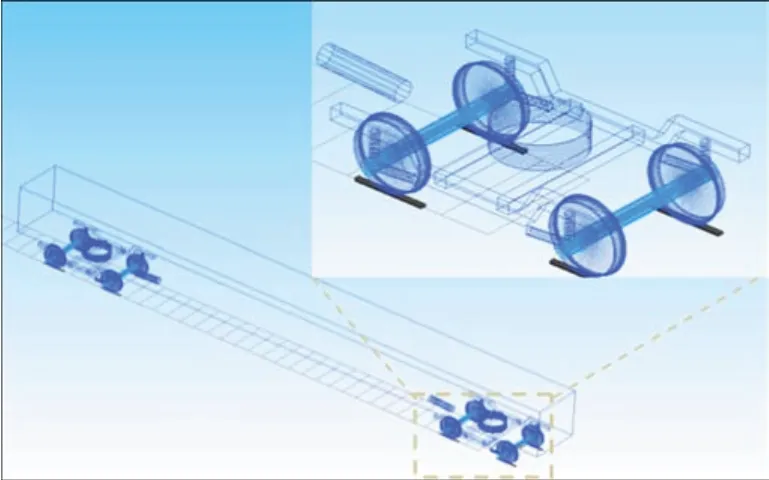
图8 车辆系统动力学模型Fig.8 Vehicle system dynamics model

具体来说，该车辆动力学模型由1 个车体、2个构架、2个牵引杆、4个轮对、8个转臂构成，共15个刚体。车体、轮对、构架有6个自由度，牵引杆有点头、摇头2个自由度，转臂仅有1个点头自由度，共计54 个自由度。轮对与构架间由一系弹簧、减振器和转臂连接，构架与车体间由二系悬挂弹簧、抗蛇行减振器、横向减振器、和牵引杆等连接，悬挂弹簧、减振器、横向止挡等均由弹簧-阻尼力元表征。

表2 车辆部分参数Table2 Part parameters of vehicle

模型中考虑轮轨标准型面和磨耗后的实测型面，仿真所用实测轮轨廓形如图9所示，其中，图9(a)所示为某动车组头车(1 车)的左侧(发生疲劳一侧)4个车轮廓形，其走行里程总58万km，镟后里程为20万km；图9(b)所示为小半径曲线的钢轨实测廓形，可见高轨侧钢轨存在明显侧磨。轮轨间摩擦因数取开放环境干态下的典型值0.3。为方便起见，模型中曲线均设为左曲线，曲线半径、超高、曲线长度等轨道参数及在相应的运行速度根据所调研线路的实际情况设置见表3。

图9 实测轮轨廓形Fig.9 Actual measurement of wheel rail profile

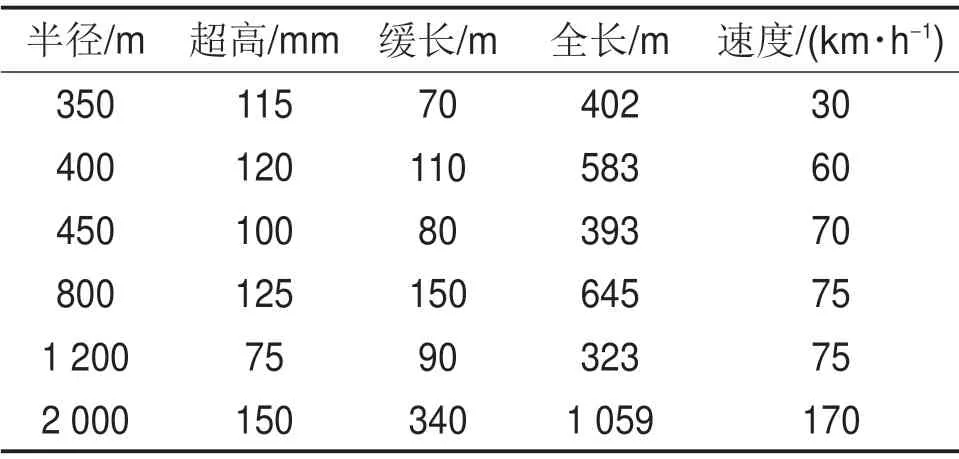
表3 仿真曲线参数设置Table3 Parameter settings of simulation curve

2.2 损伤函数预测模型

将上述动力学模型输出的各轮轨接触界面的法、切向接触结果引入损伤函数，可进一步预测车轮是否萌生滚动接触疲劳。损伤函数在以往研究中得到验证[8-13]，结果如图10所示，其中，纵坐标为损伤量，正值表示疲劳损伤，负值表示磨耗，总损伤为两者代数和，横坐标磨耗数的计算公式如下：

式中：Tx和Ty分别为纵、横向蠕滑力；γx和γy分别为纵、横向蠕滑率。本文所涉动车组的车轮材料为ER8 钢，其损伤函数中关键参数取值见图10[8]。需说明的是，只有当作用在车轮上的纵向蠕滑力方向与列车运行方向相反时才计算疲劳损伤，这主要是将轮轨接触载荷作用下裂纹闭合效应和液体润滑作用对滚动接触疲劳裂纹扩展的影响考虑在内[15-16]。

图10 损伤函数模型Fig.10 Damage function model

3 仿真结果

模拟车辆通过左曲线，各曲线设置参数见表3，选取圆曲线上10 s 的结果，分析不同工况下的车轮损伤情况。先计算新轮新轨(LMA-CN60)匹配下车轮的I类疲劳损伤，之后，分析磨耗、轨底坡波动等现场复杂因素的影响。

3.1 新轮新轨匹配

图11所示为新轮新轨匹配时导向轴(1 轴)左、右车轮损伤量随曲线半径的变化，其中，正值表示疲劳，负值代表磨耗。轮位中数字“1”代表1轴，L 和R 分别代表左、右侧。3L 和3R 车轮的损伤位置分别与1L和1R车轮的基本相同，但损伤量略低，如图12所示(因部分车轮疲劳损伤可能为0，故图中显示柱数有小于6的情况)。第2和第4轴上车轮几乎不会发生疲劳损伤，故未包含在图中。

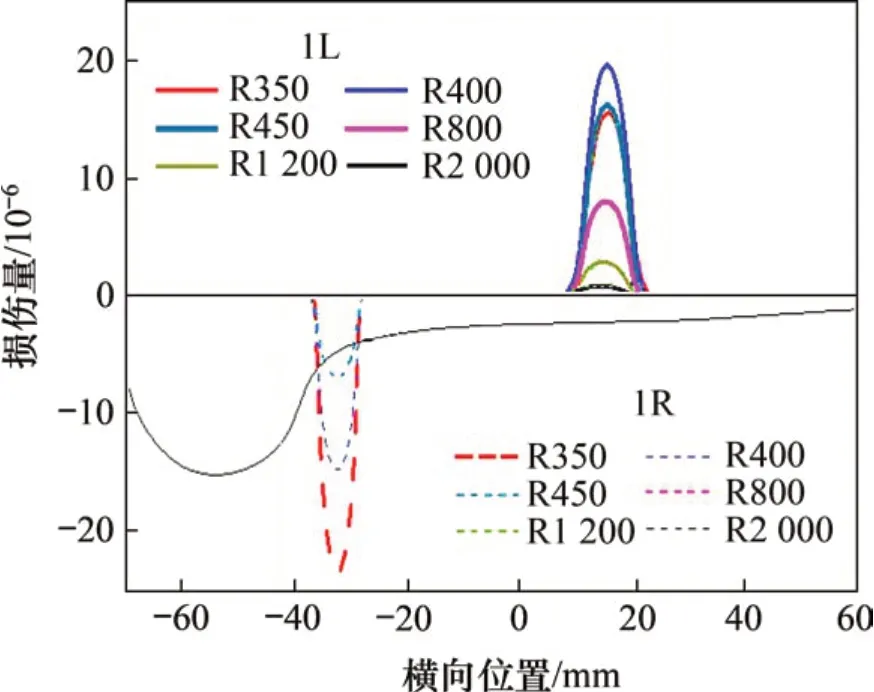
图11 导向轴左、右车轮损伤分布随曲线半径的变化Fig.11 Change of damage distribution of left and right wheels of guide shaft under different curves.

由图11可见：1L 车轮(低轨侧)会发生I 类疲劳，而1R 车轮(高轨侧)则发生轮缘磨耗，具体横向位置分别为名义滚动圆外侧7～23 mm 和内侧-29～-36 mm。此预测的疲劳区与现场实际观测位置(图4)基本相同，但分布范围更窄。从图12可见：轮缘磨耗随着曲线半径的增大而减小，而I类疲劳在400 m曲线半径时最大。产生此现象的原因是半径大于400 m时各车轮磨耗数随曲线半径的增大而单调减小(图13)，且存在损伤门槛值。具体而言，发生疲劳损伤的1L 和3L 车轮磨耗数在半径大于400 m 时位于疲劳门槛值之上、磨耗门槛值之下，而在半径小于约400 m时开始高于磨耗门槛值，磨耗的发生会抑制疲劳的发展(图10)，即曲线半径越接近400 m，疲劳损伤越大。磨耗数最高的1R 和3R 车轮，因其纵向力向后，液体对裂纹扩展的影响机制不发生作用，故表现为磨耗损伤。第2和第4轴车轮因磨耗数基本低于疲劳门槛值，也不会发生疲劳损伤。

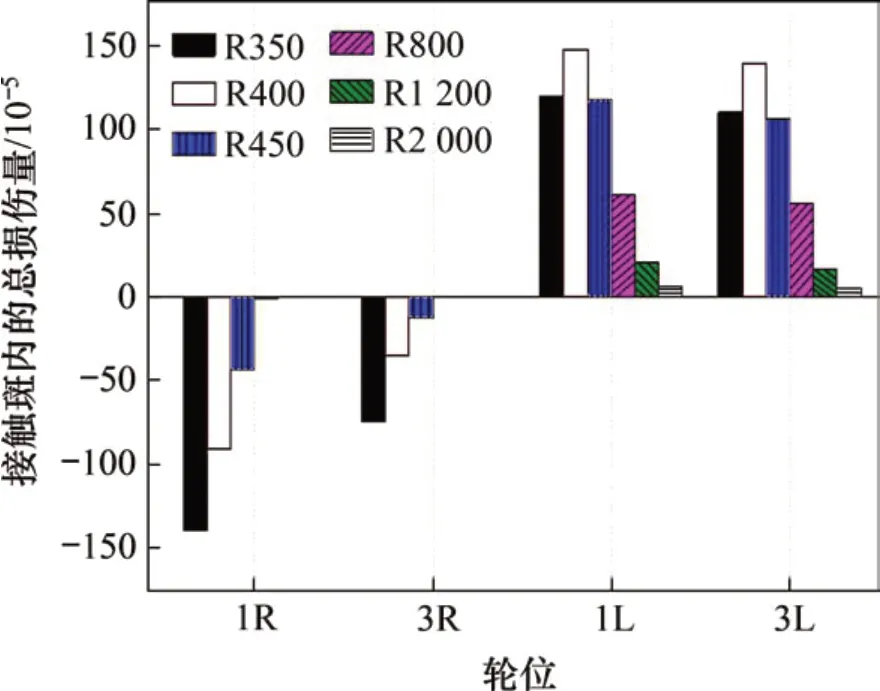
图12 各车轮损伤总量情况Fig.12 Total damage of each wheel

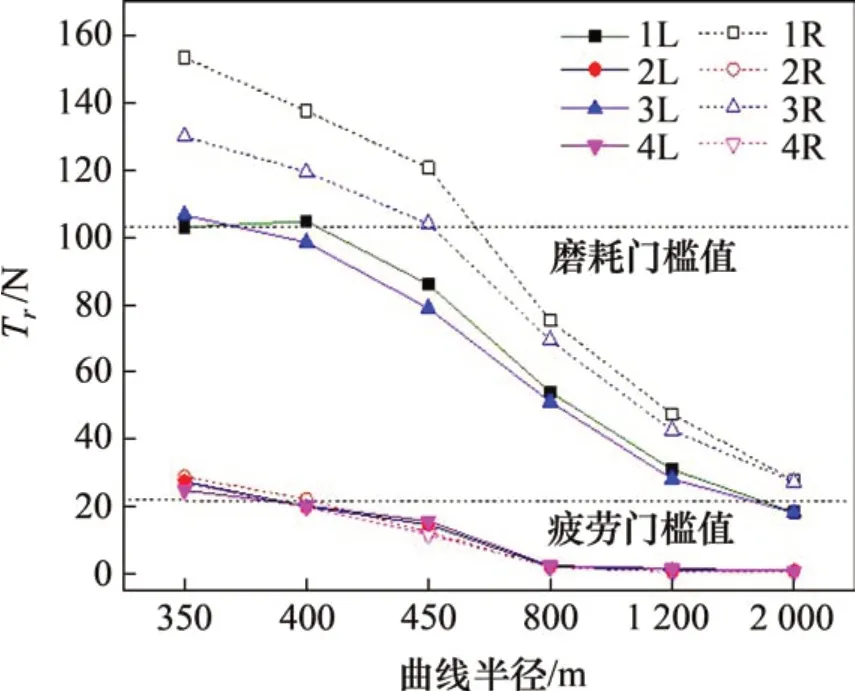
图13 各车轮平均磨耗数随曲线半径的变化Fig.13 Change of average wear number of each wheel with curve radius

综上所述，因为所调研城际线路的小半径曲线全为左曲线(图7)，所以，动车组1 轴导向通过小半径曲线时，发生疲劳的车轮为1L和3L，返程时(4轴导向)则发生在2L和4L。总之，不调头运行时，通过小半径曲线会导致I类疲劳会发生在左侧车轮上，而相应地轮缘偏磨会发生在右侧车轮上。对于全为右曲线的中半径曲线，结果与小半径曲线的刚好相反，但强度因半径更大而大大减弱，故现场最终表现出小半径曲线的损伤特征，即I类疲劳在左侧而轮缘偏磨在右侧。换句话说，小半径左曲线是导致现场观测的I类疲劳和轮缘偏磨的根本原因。定期调头运行后，I类疲劳及轮缘偏磨损伤变成由两侧车轮交替承受，即使幅值不变，观测到的I类疲劳和轮缘偏磨也会大大减轻，2019年1月的观测结果证实了这一点。此外，图12中1轴车轮I 类疲劳损伤略大于3 轴的预测结果，解释了普查中(尤其是第1次普查)I类疲劳集中于头尾车导向轴的现场观测结果。

3.2 现场复杂因素的影响

3.2.1 磨耗轮轨廓形

图14 不同轮轨匹配方式下1L车轮的I类疲劳损伤峰值和平均接触位置对比Fig.14 Comparison of RCF class I fatigue damage peak value and average contact position of 1L wheel under different wheel-rail matching methods

实际中轮轨存在新轮新轨、新轮磨耗轨、磨耗轮新轨及磨耗轮磨耗轨等不同匹配方式。以新轮新轨匹配下I 类疲劳损伤最大的400 m 半径曲线工况为例，图14(a)所示为不同轮轨匹配方式1L车轮的损伤峰值(即损伤分布图14中损伤最大值)及平均接触点位置。从图14(a)可见：不同的轮轨匹配方式损伤峰值稍有不同，某些会导致损伤峰值增高，但另外一些会导致损伤峰值降低，即轮轨磨耗与I类疲劳损伤峰值之间不存在简单的关系。

实测钢轨廓形有限，但车轮廓形很多，这里进一步讨论车轮磨耗量的影响，结果如图14(b)所示。从图14(b)可见：不同运行里程车轮廓形与磨耗轨匹配时，I类疲劳损伤的峰值随车轮运行里程的增加近似线性增加，平均接触点位置稍稍向外侧移动。由于所模拟小半径曲线处的外侧钢轨侧磨严重，会引起轮对曲线通过时发生向外侧的大横移，也会导致导向轴低轨侧车轮接触点位置向外侧移动。上述结果可以在一定程度上解释现场观测到的I类疲劳区逐渐向踏面外侧移动的现象。

3.2.2 轨底坡波动

仍以新轮新轨匹配为例，考虑表1中半径R为400 m的曲线实测轨底坡，与前面分析中设计值的结果进行对比，结果见图15。由图15可见：在半径为400 m曲线下，1L车轮I类疲劳损伤的发生区域和峰值均随轨底坡而呈现出显著变化。

除了轮轨廓形和轨底坡外，现场中其他参数也会不可避免地波动，也可能会对车轮I类疲劳的萌生位置和速率等产生影响，例如研磨子造成的磨耗、牵引/制动力及摩擦因数的变化等，从而进一步使现场的车轮I 类疲劳现象复杂化。换句话说，欲精确预测现场所观测的现象，需充分考虑很多不确定因素。

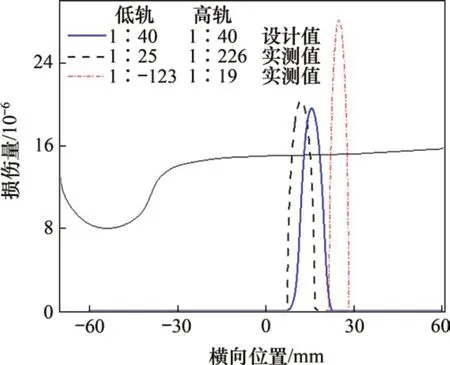
图15 1L车轮的不同轨底坡I类疲劳损伤对比Fig.15 Comparison of RCF class I fatigue damage of 1L wheel with different rail bottom slopes

4 结论

1)早期动车组不调头时，I 类疲劳在总里程(6～9)万km时出现，集中发生在左侧车轮。起初疲劳区位于名义滚动圆外侧5～15 mm 处，之后略有扩大且向踏面外侧移动。

2)列车曲线通过时低轨侧轮轨相互作用是产生I类疲劳的根本原因；当曲线半径大于400 m时，疲劳寿命随半径的增加而增加。线路上小半径曲线(R≤450 m)全为左曲线，导致调头前I 类疲劳集中在左侧车轮。

3)定期调头后，左右侧车轮交替承受疲劳载荷，从而有效地缓解了I类疲劳损伤。

4)轮轨廓形演化和轨底坡误差等是I类疲劳区扩大和向外侧移动的直接原因。