基于Burgers模型下泥岩三轴蠕变参数的辨识
张庆建 王鹏程 赵永 许春羚
岩石的力学性态不仅表现出弹性、黏性和塑性,而且具有与时间相关的性质。工程实践表明,建筑物的破坏和失稳,并不是在开挖后立即发生的,从开始变形到最终破坏是一个与时间有关的复杂的非线性累进过程,处于长期缓慢蠕变之中。合理地描述并揭示岩石时效力学行为具有重要意义。建立岩石三轴蠕变模型是研究并预测岩体长期运行工况下变形的重要手段,因此,准确进行模型参数辨识就成为关键一步。
目前,已经开展了许多关于蠕变模型的研究,对模型参数辨识方法主要有:回归反演法、最小二乘法和解析解法。徐慧宁等[1]对粉砂质泥岩一维西原模型参数进行辨识,但并未对其中黏滞系数取值问题作详细说明;王怡等[2]对花岗岩建立三维广义kelvin 模型,并导出了黏弹性理论解析解,给出了参数识别方法。朱杰兵等[3]利用嵌入L-M 算法的最小二乘法(LM-NLSF 法)对大理岩Burgers 蠕变模型进行了优化辨识。回归反演法和最小二乘法均需通过编制程序进行计算,初始值选取不当会导致迭代无法收敛。解析解法采用公式推导,使用方便,但由于岩石间的差异性和本身的非均质性,解析解法并不能很好地反演所有蠕变曲线,本文结合蠕变曲线提出一种模型参数辨识方法——图解法,并将解析解法与图解法结合,进而提出一种改进解析解法。该方法能够依据试验蠕变曲线准确辨识模型参数。考虑到泥岩蠕变变形较大,广义kelvin 模型无法描述蠕变特性,本文通过泥岩三轴蠕变试验,建立三维Burgers 模型,利用改进解析解法进行参数辨识。
1 三轴蠕变试验及蠕变模型
1.1 试样制备及试验方法
三轴蠕变试验所用试样取自某工程钻孔泥岩样,试验前加工成直径50 mm、高度100 mm 的标准圆柱体试件。试验在中水北方勘测设计研究有限责任公司TAW-2000 多功能三轴流变试验机上进行,围压为3 MPa,轴压采用分级加载进行。各级荷载持续施加的时间由试样的应变速率控制,每级应力水平下蠕变试验稳定标准应满足变形增量小于0.001 mm/d,且每级荷载持续时间不宜少于7 d,直至试样发生破坏或变形急骤增加,试验停止。
1.2 蠕变曲线及特性
本次蠕变试验分5级加载,轴向应力为4~8 MPa,级差1 MPa,图1 为低于长期强度的轴向应力所对应的应变叠加曲线。从图1 中可以看出,该泥岩的轴向应变可以分为两部分:一部分是瞬时应变,即每级应力水平施加瞬间试样产生的瞬时变形;另一部分是蠕应变,即在恒定应力水平作用下,试样随时间增长的变形。蠕应变部分由衰减蠕变阶段Ⅰ和等速蠕变阶段Ⅱ组成,等速蠕变阶段Ⅱ可看做是蠕变速率恒定,这两个阶段所对应的蠕应变正是Burgers 模型所重点描述的。

图1 泥岩轴向应变叠加曲线
1.3 Burgers模型
蠕变模型是把岩石等材料抽象成一系列简单的元件(如弹簧、阻尼器等)及其组合模型来模拟岩石的蠕变特性,并建立本构方程。
从图1 可知,在低应力水平下(σ1=4 MPa),泥岩蠕应变随时间增加而变大,即不存在明显的起始蠕变强度;轴向应力处于长期强度以前,可将泥岩简化为黏弹性材料;因此,Burgers 模型能较好地反映泥岩蠕变特性。图2 为Burgers 模型元件组合及曲线示意图,其中E1处弹簧为弹性元件,与蠕变曲线瞬时变形有关,η1处元件为黏壶牛顿体,主要在等速蠕变阶段Ⅱ发挥作用,E2和η2处黏弹并联元件为开尔文体,主要控制衰减蠕变阶段Ⅰ的变形特性。通常情况下,岩石处于复杂的三维应力状态,考虑到本次试验为三轴蠕变试验(σ2=σ3),因此,建立岩石在三维应力状态下的蠕变本构方程具有重要意义。基于广义胡克定律公式,通过拉式变换[2],三维Burgers 模型本构方程可表示为

式中K——体积模量;
G1——弹性剪切模量;
G2——黏弹性剪切模量;
η1——黏弹性黏滞系数;
η2——黏弹性黏滞系数。

图2 Burgers模型
2 模型参数辨识
2.1 解析解法
由式 1 可知,当t=0 时,ε1t=ε0;ε0可由试验数据得到,结合式(3)便可求得K和G1参数。式(1)中项产生的变形主要在蠕变曲线中等速蠕变阶段Ⅱ,η1参数与该阶段蠕变曲线斜率相关,通过最小二乘法拟合可获取η1参数。由图2 可知,令t=∞,则蠕变曲线无限接近一渐近线,渐近线可表示为
式(5)两边取对数
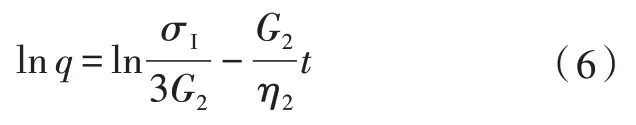
式(6)可看做是t—lnq的线性回归问题,通过最小二乘法拟合可求得G2和η2;至此便求得三维Burgers 模型本构方程所需的全部参数。
2.2 图解法及改进解析解法
由式(1)和图2 可以看出,黏壶牛顿体和开尔文体随时间的变形共同构成总蠕变量;本次蠕变试验中,在衰减蠕变阶段初期,黏壶牛顿体产生的变形仅占开尔文体变形的4%左右,到了衰减蠕变阶段末期,该比例上升至约10%,而此时开尔文体已产生95%左右的变形;显然衰减蠕变主要由开尔文体变形组成,等速蠕变主要由黏壶牛顿体变形组成。
图解法就是将模型元件和蠕变曲线根据蠕变阶段进行划分,其中K、G1和η1参数的求解与解析解法相同,求解G2和η2参数时,将Burgers 体分解为广义开尔文体和黏壶牛顿体,如图1 所示,广义开尔文体产生的变形经过衰减蠕变阶段到达j点后收敛为虚线所示,等速蠕变阶段的变形则可认为由黏壶牛顿体继续产生。令t=∞,则
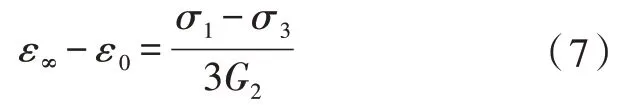
任一时刻t所对应的黏滞系数为

式(7)中ε∞可由试验数据获得,式(8)中时间t可选取衰减蠕变阶段初期。由此,G2和η2便得以求解。
为避免解析解法中t—lnq线性相关性差导致的参数G2拟合偏差以及图解法中η2主观性取值问题,本文提出一种改进解析解法。改进解析解法是将解析解法与图解法结合,首先通过图解法辨识参数G2,然后利用优定截距拟合法对t—lnq线性关系进行再拟合,此时通过式(6)即可求出参数η2。
2.3 蠕变曲线反演分析
以图1 中蠕变曲线c 为例,利用解析解法对Burgers 模型进行参数辨识,反演得到的参数如表1所示,其中t—lnq线性回归曲线如图3 所示。

表1 Burgers模型参数反演值

将反演得到模型参数代入到式1 中,得到本构方程的反演蠕变曲线,图4 给出了蠕变试验曲线和Burgers 模型反演曲线。
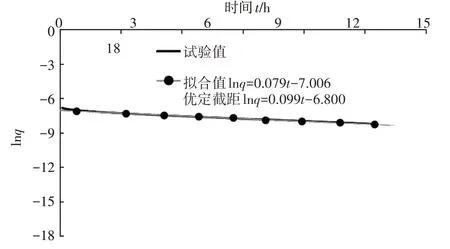
图3 t—lnq关系曲线
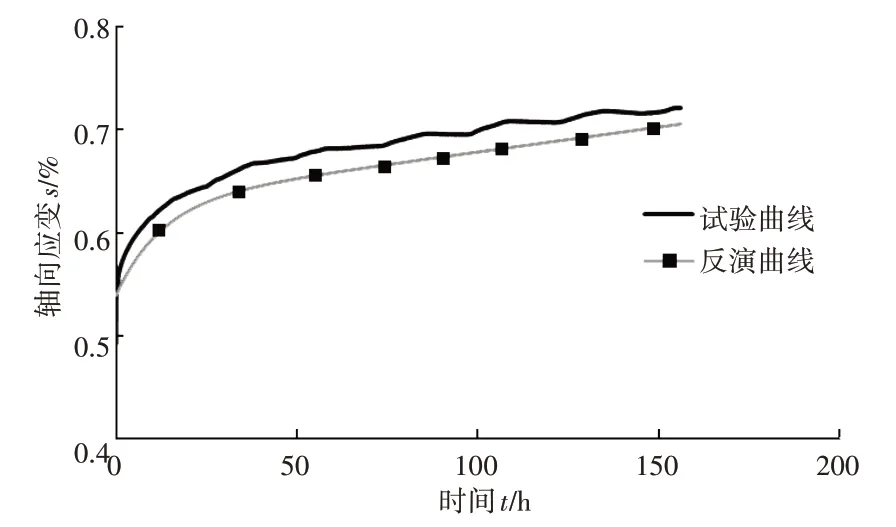
图4 泥岩蠕变试验曲线与反演曲线比较(解析解法)
从图4 可以看出,两曲线形状相似,在整个蠕变阶段,反演曲线应变量较试验曲线应变量小。这主要是由于t—lnq关系并非绝对线性,从而导致参数G2拟合存在偏差。
利用改进解析解法,对t—lnq线性关系进行优定截距拟合如图3 所示,反演得到的改进参数G2和η2见表1。将参数代入到式(1)中,重新得到反演蠕变曲线如图5 所示。从图5 可以看出,通过改进解析解法得到的反演曲线与蠕变试验曲线较吻合,反演曲线对试验曲线的拟合优度达99%,可见反演曲线能较好地描述衰减蠕变阶段和等速蠕变阶段。对比图4 和图5 还可知,参数G2和η2是决定反演曲线的重要参数,黏弹性剪切模量G2决定衰减蠕变阶段变形量大小,也影响最终蠕变量,黏弹性黏滞系数η2影响衰减蠕变阶段曲率,决定达到等速蠕变阶段时间的长短,η2值越小,衰减蠕变阶段曲率越大,达到等速阶段时间越短,反之达到等速蠕变阶段时间越长。
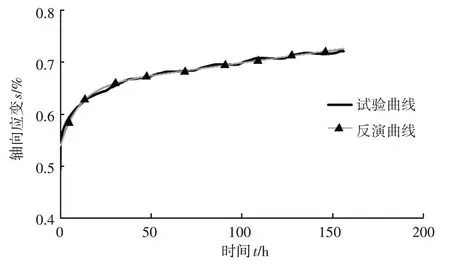
图5 泥岩蠕变试验曲线与反演曲线比较(改进解析解法)
通过上述Burgers 模型参数反演,验证了改进解析解法的适用性,也验证了Burgers 模型描述泥岩蠕变特性的正确性和合理性,为蠕变模型参数辨识提供了新思路,以便正确认识泥岩时效变形规律。
3 结 语
三向应力状态下泥岩蠕变试验是研究工程岩体长期运行工况时效性的基础,也是获取本构模型参数进行有限元计算的重要手段。
通过模型参数辨识,改进解析解法能较好地反演模型参数,并可以直观地了解各参数的实际意义,更是深入探究了黏弹性剪切模量G2和黏弹性黏滞系数η2的重要性。同时也验证了Burgers 模型作为泥岩蠕变模型的合理性。

