基于数据匹配的机载外挂装备部件振动试验优化设计方案

王东升，李 翀，李 健，欧阳智江，吴连军，刘青林，蒋华兵

（中国工程物理研究院 总体工程研究所，绵阳 621900）

0 引言

喷气式飞机外挂装备通过吊耳、挂架悬挂在机翼下方。该类装备的振动试验按照GJB 150.16A—2009《军用装备实验室环境试验方法 第16 部分：振动试验》的规定应采用程序IV（组合式飞机外挂的挂飞和自由飞）方法进行[1]，即用外挂悬挂设备（炸弹架、发射器和挂架等）把装备悬挂在结构支撑架上，采用两点激励试验方法。某机载外挂装备由部件及发动机构成。在装备的研制过程中，由于部件与发动机研制进度不同步或试验设备能力不满足要求等原因，有时不具备对整个装备进行振动试验的条件，需要单独对部件进行试验。但由于吊耳位于发动机上，单独对部件进行振动试验时无法悬挂，所以不能采用程序IV 的试验方法，可选择该标准中程序I（一般振动）方法单独对喷气式飞机外挂装备的部件进行振动试验。

而采用程序I 方法对某装备部件进行振动试验后，发现该部件功能失效，但在实际挂飞中该部件却工作正常。为了分析部件失效的原因，对比了振动试验响应数据及实际挂飞测试数据，结果发现：试验中装备上的响应规律与实测数据不符，试验中失效部件处的振动响应大于实际飞行的振动响应。由此可见，虽然振动试验通常遵循覆盖实际环境的原则，但简单地按照程序I 方法对部件开展振动试验，可能会导致对其环境适应性考核偏严，存在过试验的弊端。

上述标准的6.4.5.1 中b）条提出了数据匹配程度的概念，即振动试验响应数据与飞行实测数据的近似程度。基础激励下结构的振动响应由载荷及结构的频响函数决定。从工程的角度分析，振动试验中影响部件振动响应的主要因素有控制方案、加载部位及载荷传递路径、夹具与部件的频响函数。因此，振动试验中的数据匹配问题实质是已知载荷和响应、求频响函数，属于结构动力学逆问题。

为了使振动试验更加符合实际情况，避免过试验，提出了部件振动试验响应与实测响应匹配程度的要求。对此，本文在载荷及系统频响特性两方面开展研究：首先通过有限元仿真，研究不同振动控制方式、载荷输入部位对部件响应的影响；之后对夹具结构进行设计优化以更真实模拟装备的频响特性；最后对该方法进行试验验证。

1 数据匹配要求

在某机载外挂装备（见图1）实际挂飞试验中，在部件的加强框1 框、2 框上进行了加速度响应测量。在实验室振动试验中期望A1～A4 的加速度响应尽可能接近实测数据。参照GJB 150.16A—2009《军用装备实验室环境试验方法 第16 部分：振动试验》的6.2.2.5 条，对不同用途的加速度测点进行了分类：将有挂飞实测数据的测点A1～A4 定义为目标点，从目标点中选取用于规定振动载荷条件的点定义为控制点，选取用于试验或仿真数据与实测数据对比的点定义为监测点。

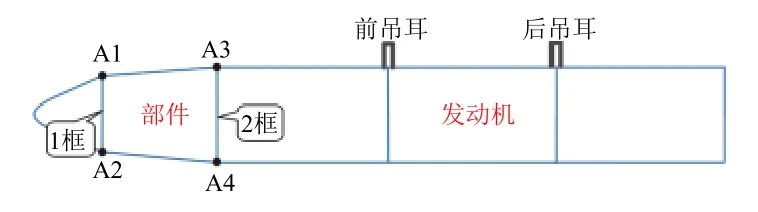
图1 喷气式飞机外挂装备示意Fig.1 An equipment hanging outside of a jet plane

为了量化振动试验数据与实测数据的近似程度，引用了GJB 150.16A—2009《军用装备实验室环境试验方法 第16 部分：振动试验》6.4.5.1 中b）条的数据匹配程度的概念。控制点的数据匹配程度通过试验条件及允差量化。监测点的数据匹配程度要求需要另做规定。

数据匹配的参数可以选择测点加速度功率谱密度、均方根值或不同点加速度均方根值的比例等[2]。从工程角度考虑其实现的难易程度及可行性，选择了1 框与2 框测点加速度均方根值平均值的比例作为匹配的参数。A1、A2 实测加速度均方根的平均值约3g，A3、A4 两点的约2g。振动试验中要求A1、A2 两点的加速度均方根值的平均值是A3、A4 平均值的(1.5±0.3)倍，即为满足数据匹配要求。

2 数据匹配的实现

2.1 控制方案

不同的控制方案对结构的输入载荷不同。选择合理的控制方案有助于在试件目标位置上产生所要求的振动量值。

当已有外挂实测振动响应数据时，飞机组合外挂通常采用加速度响应控制方法。该方法可以用试件外表面或试件内目标点的响应来规定振动条件。根据某机载外挂装备部件实测飞行数据的测点位置，确定了三种控制方案：方案一为A3、A4 两点平均控制，A1、A2 作为监测点；方案二为A1、A2 两点平均控制，A3、A4 作为监测点；方案三为A1～A4 四点平均控制。在试验方案阶段采用不同控制方案进行随机振动仿真分析，比较部件仿真数据与实测飞行数据的匹配程度，以选择数据匹配程度满足要求的方案进行试验。

2.2 加载部位及载荷传递路径模拟

GJB 150.16A—2009 的6.4 条对试件在不同工况下的安装做出了规定，对于机载外挂部件振动试验分为程序I、程序IV 两种情况。

对于程序I，处于工作中的装备规定为“用与寿命周期内工作使用时相同类型的固定装置，把试件固定在试验夹具安装部位上”。挂飞时部件通过2 框与发动机连接，按照程序I 规定夹具应与部件2 框连接，参照该规定设计了夹具1（见图2）。采用夹具1 进行振动试验时，载荷的施加部位在2 框，并从2 框传递到整个部件。

图2 夹具1Fig.2 Fixture A for the vibration test

程序IV 则规定用外挂悬挂设备把试件悬挂在结构支撑架上，由于无法悬挂，所以需要重新考虑夹具与试件的安装形式。喷气式飞机外挂装备振动载荷来源于喷气飞机噪声、外挂表面的气动湍流、通过结构传递到外挂物上的载机振动，以及内部装备和局部气动力4 个方面，其中外挂表面的气动湍流是外挂振动的主要来源。从载荷的主要来源看，应在部件的外表面施加载荷，通过加强框使载荷传递到整个部件。而夹具1 只在2 框对试件进行激励，对载荷作用部位的模拟不真实，无法反映部件前后载荷的差异。因此，为了模拟程序IV 气动载荷的作用效果，设计了夹具2，部件的1 框、2 框与夹具包带连接，见图3。采用夹具2 试验时振动台通过夹具激励部件外表面，振动载荷通过加强框传递到产品各处，能够相对更为真实地模拟载荷的作用部位和载荷的传递路径。

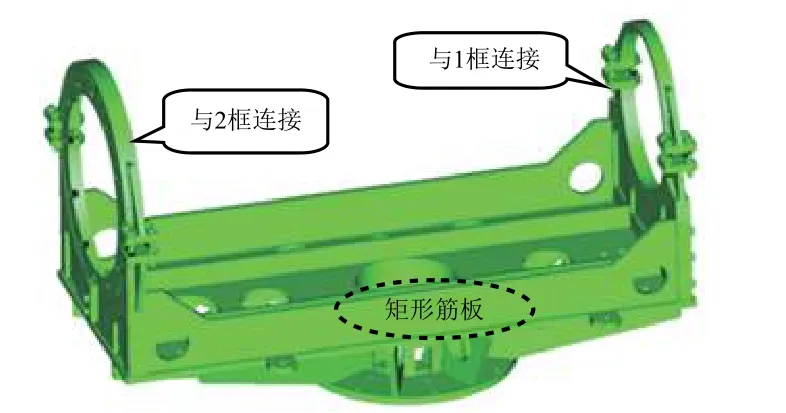
图3 夹具2Fig.3 Fixture B for the vibration test

为了比较夹具1、夹具2 及3 种控制方案的数据匹配情况，进行了随机振动仿真，结果见表1 及表2。从表1 可以看出，采用夹具1 进行试验时，三种控制方案控制结果均不能实现数据匹配；虽然采用A3、A4 两点平均控制时，1 框响应相对于2 框放大，似乎与实测规律一致，但是1 框响应相对2 框放大远超出实测数据差异，易导致严重过试验。从表2 可以看出，采用夹具2 及3 种控制方案，1 框响应相对与2 框均呈衰减趋势，但采用A3、A4 两点平均控制的衰减很小。考虑到夹具2 可以更改两端包带的结构特性，通过优化夹具有可能实现数据匹配，因此最终确定采用夹具2 和A3、A4 两点平均控制方案进行设计优化。

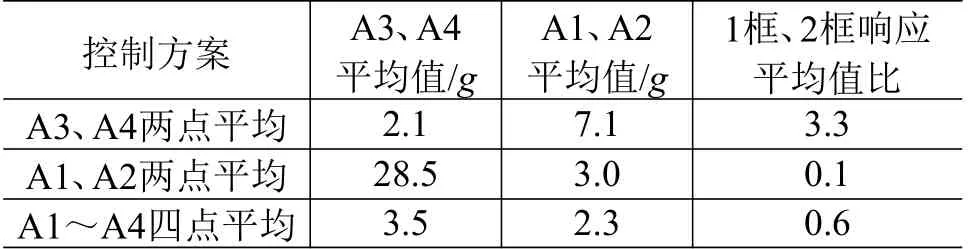
表1 采用夹具1 时的数据匹配程度Table 1 Matching degree of the response data using fixture A

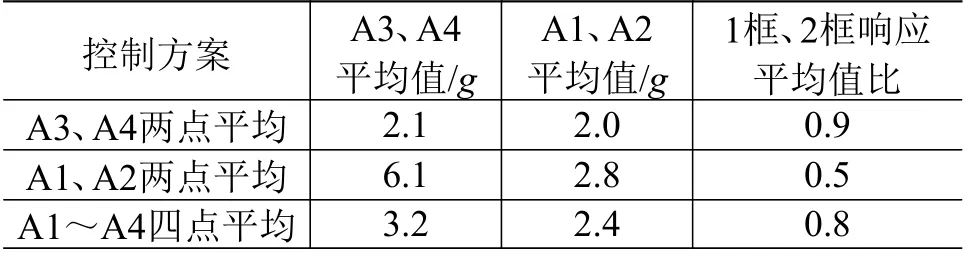
表2 采用夹具2 时的数据匹配程度Table 2 Matching degree of the response data using fixture B

2.3 振动响应优化

在控制点载荷确定的情况下，实现监测点振动响应数据的匹配是一个响应优化的过程，由于这一过程是通过改变夹具的结构形式、几何参数、材料参数实现的，因此响应优化实质上是一个夹具频响函数优化的过程[3-6]。通过优化设计或根据经验进行多方案优选的方法可以实现该目的，在工程实际中可以根据问题的难易程度、进度、经费等情况决定采用何种方法。

采用优化方法时需要确定目标函数、设计变量、约束条件等，建立振动响应优化的数学模型并进行优化求解，最终获得优化结果。

1）确定优化目标

优化目标决定了频响函数模拟的真实程度。最真实的模拟是实现目标点加速度功率谱的匹配，这要对模态频率、振型、模态阻尼比等进行模拟[7]，但由于夹具受连接边界、质量、设计时间、经费等诸多条件的限制，实现加速度功率谱的匹配十分困难。而加速度均方根值或不同点比值的匹配方法是将模态频率、振型、模态阻尼比的优化效果综合在一起，通过加速度均方根值反映出来，其对实际情况的模拟相对粗糙，然而实现起来相对容易。在实际应用中可以根据具体情况选择优化目标。

在随机振动载荷作用下，以部件1 框上m 个点加速度均方根平均值相对2 框p 个点的倍数与数据匹配要求值差的绝对值为优化目标，可建立函数

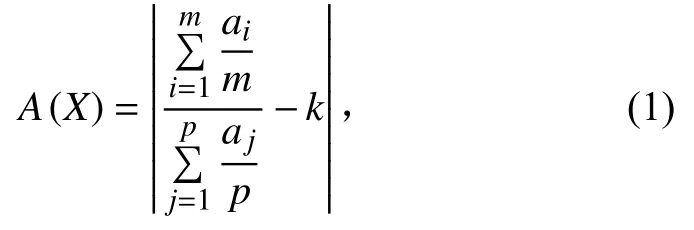
式中：ai为部件1 框上第i 点处的加速度均方根值；aj为部件2 框上第j 点处的加速度均方根值；k 为数据匹配要求值，本文为1.5。

函数A(X)越小，部件在试验中的响应数据与实测数据的差别就越小。因此，在随机振动载荷作用下优化部件加速度响应数据匹配的目标函数为

2）确定设计变量

设计变量可选用夹具的几何尺寸及弹性模量、密度、阻尼比等材料参数。在夹具优化设计前，从结构的动态性能出发，并充分考虑其与部件连接、与振动台连接、夹具与部件组合质心对中、装配干涉、起吊等因素，确定其结构形式。用一组结构参数、材料参数来表征结构的可变因素，则设计变量为

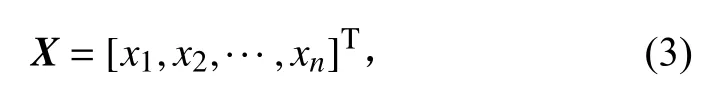
式中n 为参数数量。

3）确定约束条件

约束条件通常包括几何参数、材料参数、强度、刚度和质量约束。几何约束的作用是保证产品安装、与其他部件连接合理性和工艺合理性。材料参数约束的作用是保证材料的选择、制造的可实现性。几何约束、材料约束可表示为式(4)。质量约束是要求结构的总质量不超过一个质量上限m0，此约束的作用是将有限的材料分配到合适的部位，以满足响应优化要求。结构的质量约束可表示为式(5)。

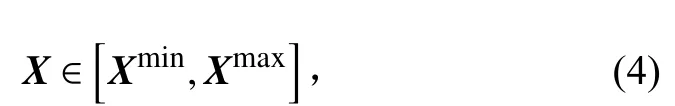
式中：Xmin和Xmax分别为几何参数、材料参数向量X的下限和上限。

总之，结构在随机振动载荷作用下的响应优化问题可以描述为：求设计变量X=[x1, x2, …, xn]T；满足约束条件X∈[Xmin, Xmax]和m(X, ρ)≤m0；使得目标函数A(X)→min。

采用多方案优选方法时，首先根据经验设计几种不同方案的夹具，再通过有限元分析结果，选择一种最优结果。

通过不同方案的有限元分析发现：对数据匹配影响最大的是与1 框连接的夹具立板及包带材料的弹性模量，降低夹具上靠近部件1 框的刚度能够使部件1 框响应增大。故可以通过改变该部位筋板的结构形式，或降低立板及包带的弹性模量来实现该目的。

将连接1 框、2 框的筋板由矩形（见图2）改为三角形并缩短了尺寸，以降低夹具连接1 框一侧的刚度，设计了夹具3（见图4）。将1 框立板的材料由钢改为铝，对包带的弹性模量进行了优化，优化后的结果见表3，满足数据匹配程度要求。

图4 夹具3Fig.4 Fixture C for the vibration test

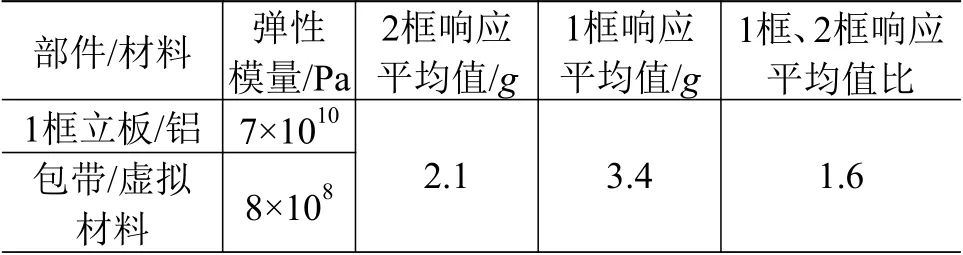
表3 采用夹具3 时的数据匹配程度Table 3 Matching degree of the response data using fixture C

2.4 夹具与部件连接部位刚度连续可调的实现

由于1 框处夹具包带优化后的弹性模量为一种虚拟材料的，该材料实际并不存在，所以如何在振动试验中实现虚拟材料的性能，以及夹具与部件连接部位刚度的连续可调是需要解决的问题。为此，在夹具2 与部件1 框连接的立板加包带结构改为立板加顶块连接方式，如图4 所示。整个夹具除1 框立板和顶块外均为钢材料，小端框立板为铝材料，顶块材料优化后为一种弹性模量介于铝与橡胶之间的虚拟材料。由于橡胶受到压缩时其刚度会提高，所以将顶块设计为一部分为铝，一部分为橡胶，通过改变顶块螺栓的拧紧力矩，能够调节橡胶的压缩量，实现该部位连接刚度的调节。橡胶的阻尼大于金属，对共振峰还有显著的抑制作用。因此可以通过在试验中调节顶块的预紧力来实现数据匹配。

3 试验验证

应用第2.3、2.4 节优化试验方案法对某机载外挂装备的部件进行了振动试验，试验采用A3、A4 两点平均控制方案，A1、A2 作为监测点，采用图4 所示的夹具。试验中夹具与1 框连接部位刚度调节采用铝加橡胶顶块方式，最终确定的拧紧力矩为20 N·m。控制曲线见图5，加速度总均方根值见表4。试验结果表明：1 框2 个监测点响应平均值相对于控制点A3、A4 的放大倍数为1.3，试验数据与实测数据的匹配程度满足要求。

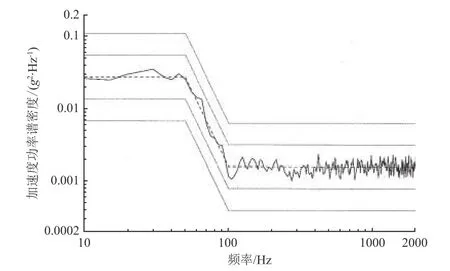
图5 振动试验控制曲线Fig.5 The control curve for the vibration test

表4 采用优化方案的振动试验数据匹配程度Table 4 Data matching degree for vibration test with optimized scheme

4 结束语

针对某喷气式飞机外挂装备的部件振动试验中的过试验问题，提出了试验响应数据与实测数据的匹配程度要求。通过优选控制方案、加载部位及传递路径模拟、夹具频响特性模拟等方面的研究，实现了预期的目的。振动试验验证结果表明，基于数据匹配的机载外挂装备部件振动试验优化方案能够更加真实地模拟装备在实际挂飞环境的振动响应，可以有效避免过试验。

本文方法对于希望提高振动环境模拟的真实性，以数据匹配为目标的各种装备的振动试验均具有借鉴意义。