直角坐标系中雷达测量方差的两种计算方法

高 效，董光波，张向荣

（1. 中国人民解放军93209 部队，北京 100085； 2. 西北核技术研究所，西安 710024）

0 引言

在分布式雷达情报组网系统中，存在2 种应用较多的坐标系：以雷达为原点的极坐标系和以指挥处理中心为原点的直角坐标系。一般认为，极坐标在近区容易产生较大的伪加速度，而直角坐标系下能得到更高的估计精度[1]，故多雷达数据融合与目标状态估计方法主要在直角坐标系下进行研究。测量方差是指单雷达极坐标系中距离、方位和仰角上的测量标准差。它是卡尔曼滤波等诸多目标跟踪算法的重要输入参数，对它的准确描述是各类滤波算法实现准确估值与稳定跟踪的前提条件。在多雷达数据融合算法中，数据融合的实际物理意义即合理地分配传感器的权重系数，而精确描述系统中的测量噪声是获得良好状态估值的一个必要条件[2-3]，因此，测量方差是确定多雷达数据融合权值的重要依据。另外，测量方差在解决测量精度不同、点迹数不同的航迹间的关联问题时同样具有至关重要的作用[4]。

测量方差一般是根据所采用传感器的精度预先设定[2]，通常以雷达出厂或校飞后确定的距离、方位和仰角测量方差作为固定参数参与航迹滤波、关联或融合计算。但须注意的是，在雷达方位测量误差相同时，目标在直角坐标系中的位置测量误差与极坐标系中的测量距离成正比。例如，警戒雷达探测到50 km 远的目标，则方位偏差1°将产生873 m的误差，探测到500 km 远的目标，就将产生8730 m的误差[5]。这意味着对于两部具有相同的方位测量方差的雷达，距目标较近的雷达测得的目标位置数据比距目标较远的雷达的测量值可信度要高，因此，以定值表示的极坐标测量方差确定雷达测量权重的方法存在不合理性。将雷达在极坐标系下的测量转换到直角坐标系下，是诸多航迹滤波、关联和融合算法的前提，同样，将雷达在极坐标系下的测量方差转换成直角坐标系下的目标位置误差，是保证各类航迹滤波和加权融合算法稳定有效的重要措施之一。然而，目前多数情况下仍将雷达极坐标测量方差作为多雷达测量加权的主要依据，对直角坐标系中目标位置测量误差的分析和研究还相对较少；诸多文献对测量方差的使用较多，但是对极坐标系到直角坐标系的转换计算方法鲜有涉及。

针对以上情况，我们提出了依据雷达极坐标测量标准差和采用雷达极坐标测量数据估计直角坐标系中目标位置误差的2 种转换计算方法，并结合相关滤波方法进行试验验证。这2 种方法分别称为误差传递法和基于直线航迹线参数估计的统计学方法（下简称“统计学方法”）。

1 误差传递法

雷达出厂或校飞后通常会给出其距离、方位和仰角上的测量标准差，我们采用误差传递定律一般式，可以计算得到每个测量点在统一直角坐标系中的x、y、z 方向上的标准偏差，进而得到目标位置间接测量标准差，此法我们称之为误差传递法，具体描述如下。

雷达R 对目标的1 个位置观测点（距离、方位、仰角）用极坐标(ρ ,θ,α) 表示，距离ρ、 方位 θ和仰角α的测量标准差分别为 σρ、 σθ和 σα。在忽略地图投影转换误差影响的情况下，统一直角坐标系中的目标位置坐标的间接测量可表示为

其中 (XR,YR,ZR)为雷达R 在统一直角坐标系中的位置坐标，在选定雷达阵地、固定地图投影模型的情况下可以看做常量。则目标在统一直角坐标系中各坐标分量上的标准差 σx、 σy和 σz按照误差传递定律一般式[6]可表示为：

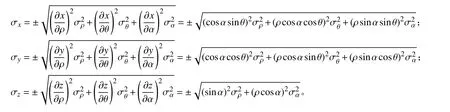
将各坐标分量上的间接测量看做等精度测量，则目标在三维统一直角坐标系中的位置误差均方根可采用真误差法、贝塞尔公式和彼得斯公式等方法求得[6-7]。本文按照最简单的真误差法[6]计算位置测量的误差均方根

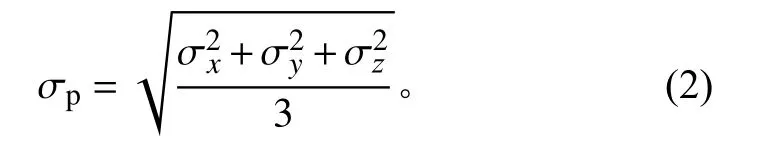
2 统计学方法

如雷达经过校准且状态稳定，则可以采用式(2)得到直角坐标系中的目标位置测量标准差。但在多雷达组网应用系统中，广泛使用的是二维直角坐标系，同时，雷达老化以及自身设计中无法预料的测量误差、不同阵地环境对雷达周边不同空域测量产生的影响、大量部署的两坐标雷达缺乏仰角测量数据以及分布式系统大区域地图投影产生的坐标转换误差等，使每个单雷达测量点经统一直角坐标转换后都产生了x、y 方向上的不同分布特征的误差，这就需要通过统计学方法计算单雷达测量在二维直角坐标系中不同区域的样本标准偏差。其中，统计样本数据来自日常观测积累，而对于不同样本数据可能获得不同的标准差，需要按区域进行聚类、平均处理。工程应用中需要经过大量统计和平均，建立对应不同典型气候环境（春、夏、秋、冬、云、雨等）、不同探测区域（例如按照探测距离ρ 和探测方位θ 分区）的测量方差估值表，在一组固定测量方差估值不能涵盖所有条件的情况下，就要具体问题具体分析，因地制宜开展应用。对此，我们给出基于直线航迹线参数估计的统计学方法，计算雷达测量在二维统一直角坐标系中x、y 方向上的样本标准偏差，进而得到目标位置间接测量标准差。

2.1 建立单雷达加权直线航迹线参数迭代估计模型[8]

某时间段内单雷达观测到直线航路上的某一飞行目标的总点数为n，所有测量点转换到二维统一直角坐标系后表示为 {(xi,yi)，i=1,2,···,n}。定义单一测量点 (xi,yi)对目标航迹线参数估计的贡献率为该点的权值，记为νi。首先按照以下方法计算单一测量点的初步权值。

基于直线方程一般式 y−k0x−d0=0，测量点(xi,yi)到直线的垂直距离为

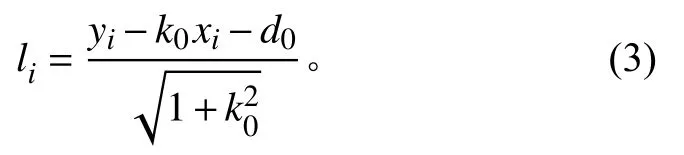
用所有单雷达观测点{ (xi,yi)，i=1,2,···,n}到该直线的垂直距离li的平方和最小作为条件构造直线，计算在此条件下这条直线的最佳参数 (k0,d0)，即为不加权直线航迹线参数估计模型

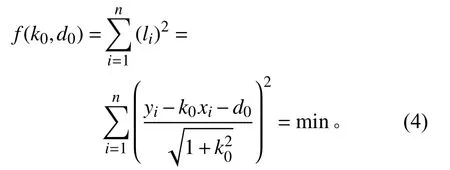
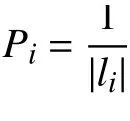
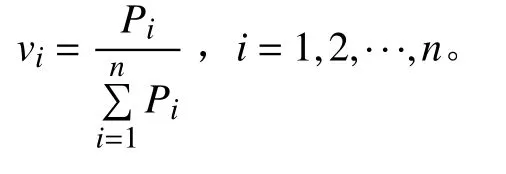
在νi已知的基础上，同样基于直线方程一般式，用所有单雷达观测点{ (xi,yi)，i=1,2,···,n}到某直线的垂直加权距离 (vi×li)的平方和最小作为条件构造直线，计算在此条件下这条直线的最佳参数 (k,d)，即为单雷达加权直线航迹线参数估计模型

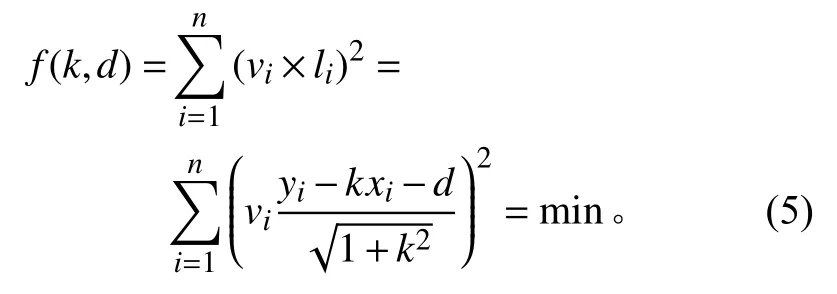
对于式(5)的求解，可以构造方程

求解式(6)，可以得到一组合理的直线参数解 (k,d)。然后计算所有测量点 (xi,yi)到新直线的加权距离之和

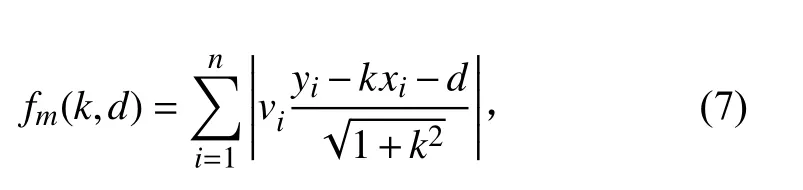
直到 fm(k,d)不 再减小为止，此时的 (k,d)即为最佳直线参数；否则按照当前 (k,d)重新计算所有测量点(xi,yi)的最新权值νi，回归对式(5)的求解过程。式(7)中的m 表示迭代次数。

2.2 计算目标在x、y 分量上的雷达观测航迹线参数

选取雷达在典型航路（目标作匀速直线运动）上对某一目标的一组观测点数据{(ti,ρi,θi,αi)，i=1,2,···,n} ，其中 (ρi,θi,αi)分别表示ti时刻雷达测量到的目标极坐标距离、方位和仰角（对于两坐标雷达，认为所有测量点的仰角均为0）。采用式(1)同时忽略高度影响，将极坐标数据转换到二维统一直角坐标系下，得到{ (ti,Xi,Yi)，i=1,2,···,n}。

将x 轴运动分量 {(ti,Xi)，i=1,2,···,n}简记为{(xi,yi)，i=1,2,···,n}，采用单雷达加权直线航迹线参数迭代估计模型计算目标在x 方向上的直线参数( kx,dx)， 得到运动状态方程y −kxx−dx=0。

将y 轴运动分量 {(ti,Yi)，i=1,2,···,n}简记为{(xi,yi)，i=1,2,···,n}，采用单雷达加权直线航迹线参数迭代估计模型计算目标在y 方向上的直线参数( ky,dy)， 得到运动状态方程y −kyx−dy=0。

2.3 计算目标在x、y 分量上的测量标准差

将x 轴运动分量 {(ti,Xi)，i=1, 2, ···, n}简记为{(xi,yi)，i=1,2,···,n}， 计算样本点{(xi,yi)，i=1,2,···,n}到 直线y =kxx+dx的平均距离

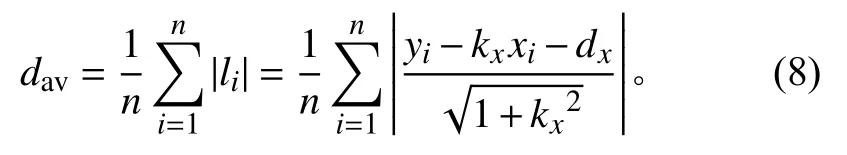
计算样本点 {(xi,yi)，i=1,2,···,n}到直线y =kxx+dx的 距离的标准偏差 σx，即为雷达测量在x 坐标分量上的样本标准偏差，

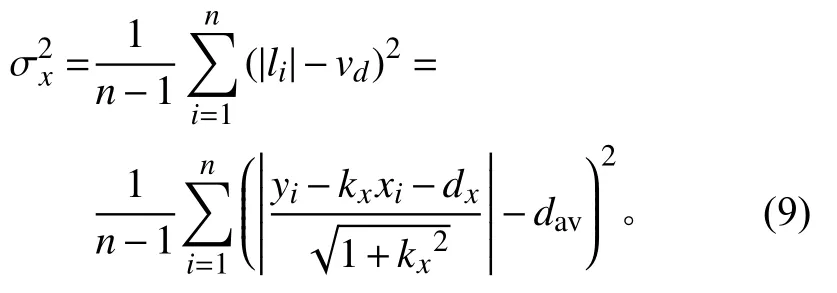
同样，将y 轴运动分量{ (ti,Yi)，i=1,2,···,n}简记为{(xi,yi)，i=1,2,···,n}， 根据参数( ky,dy)，仿照式(8)、(9)得到样本点到直线 y=kyx+dy的距离的标准偏差σy，即为雷达测量在y 坐标上的样本标准偏差。

按照真误差法[6]计算目标在二维统一直角坐标系中的位置测量误差均方根为

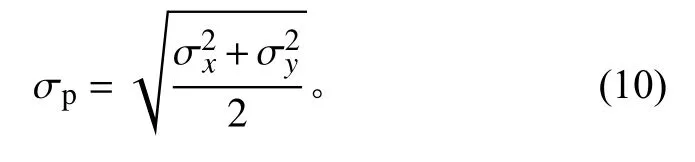
3 应用与实践

在模拟环境中使用本文提出的误差传递法和统计学方法对二维直角坐标系中多部雷达测量方差进行了计算，并将计算结果应用于多雷达双层加权直线航迹线融合模型中。图1 是在二维直角坐标系中采用本文提出的2 种雷达测量方差计算方法参与多雷达测量数据权值动态分配后的多雷达航迹融合结果。试验表明，各雷达测量方差对其测量数据权值动态分配起到了关键作用，航迹融合均取得了预期效果。另外，由于试验环境中存在大量两坐标雷达，以及误差传递法缺乏仰角测量数据等原因，雷达测量方差计算的准确度不及统计学方法，造成其多雷达航迹融合效果略逊于后者。

图1 两种雷达测量方差计算方法在多雷达加权航迹融合模型中的应用效果Fig.1 Application of two kinds of calculation methods for the variance of radar measurements in the multi-radar weighted track fusion model

4 结束语

本文提出了依据雷达极坐标测量标准差（误差传递法）和采用雷达极坐标测量数据（统计学方法）估计直角坐标系中雷达测量方差以及目标位置误差这2 种计算方法，并应用于多雷达双层加权直线航迹线融合模型中的雷达测量权值动态分配过程中，均取得了良好效果。其中，误差传递法适用于经过校准且状态稳定的三坐标雷达，要求雷达测量误差分布特征较为一致；统计学方法对于雷达的适用条件更加宽松，但对于统计数据有一定要求（目标作匀速直线运动时的观测数据）。这2 种雷达测量方差估计方法对于卡尔曼滤波器等传统滤波器和多雷达航迹关联算法也具有较高的推广和应用价值。另外，本文得出的雷达测量方差是指测量标准差 σ，对于工程上取值 3σ（置信区间为99.7%）或2σ（置信区间为95%）的极限误差估计同样适用。