不同钢-混凝土组合柱力学性能的数值分析
杨正俊
(无锡汽车工程高等职业技术学校,江苏 无锡 214153)
近年来,由于钢-混凝土组合结构体系能够结合钢材以及混凝土的优势,已广泛应用于桥梁、建筑结构以及地震频发区域。因此,钢-混凝土组合结构受到越来越多的关注[1]。
目前,传统形式的钢-混凝土组合柱有两种,分别为型钢混凝土(SRC)柱和钢管混凝土(CFT)柱。在SRC柱中(图1a),外包混凝土可以防止型钢的局部屈曲并增强结构的耐火性,核心的型钢则能够有效提升柱的抗剪能力。然而,置于截面中心的型钢其抗弯能力不能被充分发挥,并且结构整体的现场施工比较复杂。对于CFT柱,内部填充的混凝土可以有效防止薄壁钢管的局部屈曲,且外包钢管可以约束核心混凝土并提升其抗压强度。但CFT柱由于钢管外露,因而其抗火性能较弱。
鉴于此,有学者提出在CFT柱外侧包裹约束混凝土(RC),形成CFST柱(图1b)。其具有较好的抗火及耐腐蚀性能,并且外部的约束混凝土能够有效延缓钢管的屈曲。Soliman等[2]通过对CFST和SRC柱进行轴压试验,探究不同类型柱对其受力特征的影响。韩林海通过建立三维有限元模型,分析了CFST柱在轴压下的力学性能[3]。丁发兴等[4]结合试验及数值模拟对STSRC柱进行轴压性能研究,提出了试验柱的极限承载力简化计算公式。为了增强混凝土的约束效应以及便于灌浆,Gan Dan等[5]通过设计STSRC和CTSRC柱(图1c、图1d)试件并进行低周往复分析,得出这两种柱的延性及耗能均优于传统SRC柱[5]。
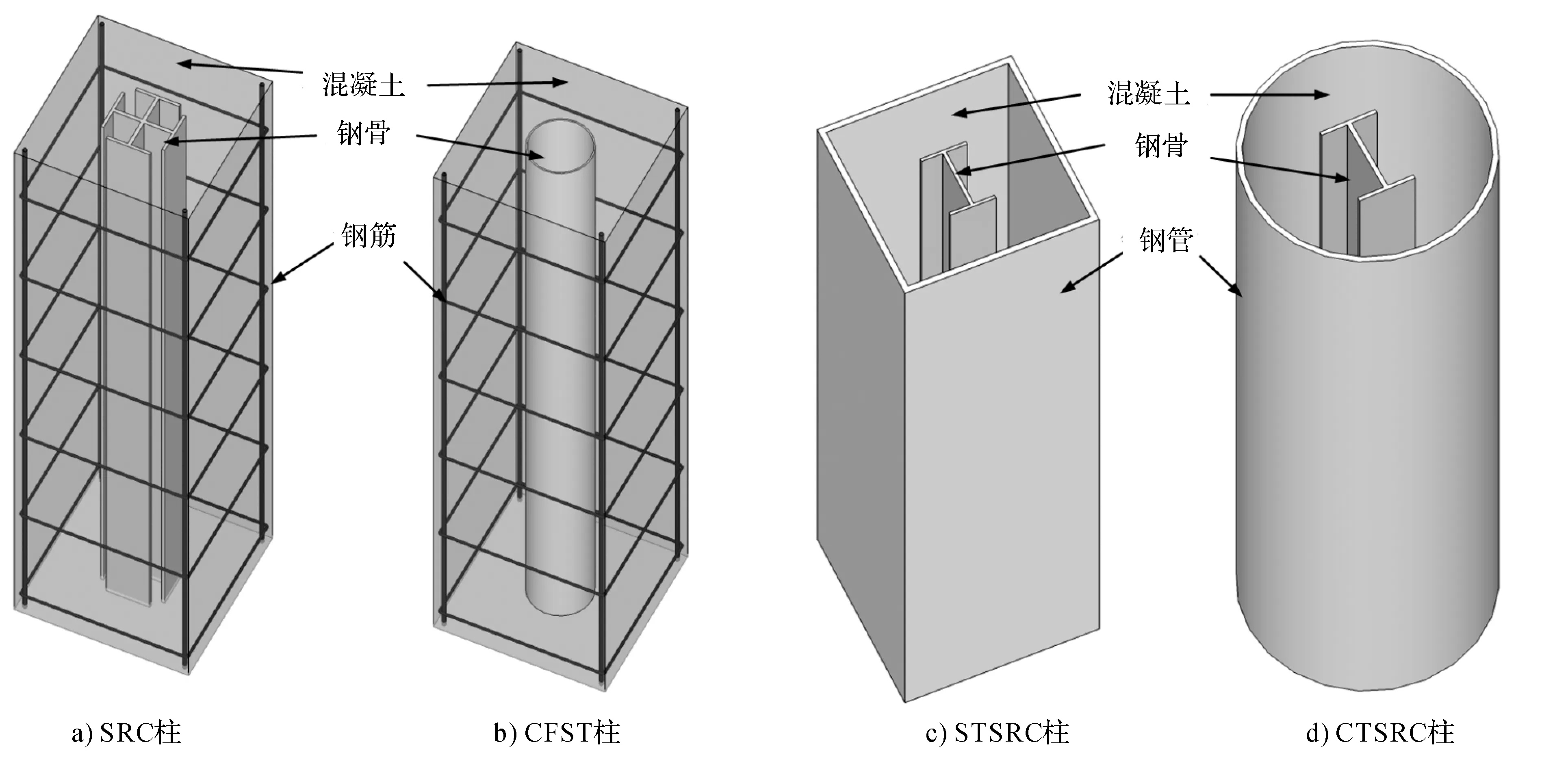
图1 钢-混凝土组合结构柱
本文利用有限元软件ABAQUS对比分析了在轴压作用下SRC、CFST、STSRC以及CTSRC柱的破坏状态、荷载-位移曲线、承载力以及延性性能,并同时探究了不同截面柱内置型钢的约束效应,旨在为不同截面组合柱在实际工程中的应用提供参考和借鉴。
1 试件设计
本文共设计4个试件进行数值计算模拟,SRC(S1)、CFST(S2)、STSRC(S3)以及CTSRC(S4)的基本尺寸及细节构造见图2。其中,S1和S3的型钢及钢管截面分别为工字型和矩形,S2和S4为圆环型。各试件的截面净高为3 600 mm,截面尺寸均为360 mm×360 mm,截面含钢率均为8.2%。对于SRC柱,型钢放置在截面中心(图2a),4根直径为12 mm的纵筋置于柱截面四角,并在其外围绑扎箍筋,箍筋直径为6 mm,间距为200 mm。CFST柱的钢筋布置与SRC柱相同,圆钢管被置于截面中心(图2b)。STSRC和CTSRC柱分别在外侧采用方钢管以及圆钢管,并在截面中心放置工字型钢(图2c、图2d)。S1~S4试件混凝土强度均为C60,型钢和钢管采用Q235钢材,钢筋采用HRB500级。
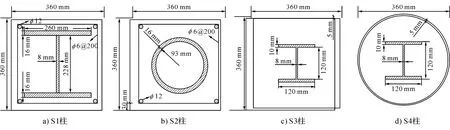
图2 截面的尺寸及细节构造
2 有限元模型
2.1 模型的建立
采用ABAQUS有限元软件对各试件柱进行模拟。混凝土、型钢以及钢管均采用8节点减缩积分格式的三维实体单元C3D8R,并采用结构化网格划分技术对其进行网格划分。采用三维桁架单元T3D2模拟纵筋及箍筋。有限元模型见图3。
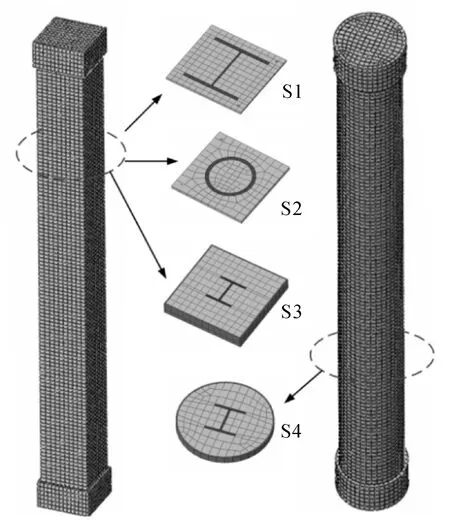
图3 有限元模型
2.2 材料模型
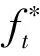
在所有试件模型中,型钢、钢管以及钢筋的应力应变关系均采用理想弹塑性模型,见图4b),其本构表达式如下:

图4 材料应力-应变关系曲线
(1)
其中,Es为钢材的弹性模量,fy为钢材的屈服强度,εy为钢材达到屈服强度所对应的应变,σ、ε分别为钢材的应力和应变。钢材的屈服强度、弹性模量取实测值,泊松比为0.3。
2.3 相互作用及加载方式
S1和S2试件模型均采用Embed约束,将钢筋固嵌到混凝土当中,并在嵌入单元与主单元之间建立节点关系;假定各模型中的型钢、钢管与混凝土之间均不产生滑移,采用tie约束将其两两绑定。
为防止柱端出现局部破坏,在柱顶和柱底设置钢帽,钢帽与试件模型进行绑定。在顶部钢帽表面建立耦合约束,并对参考点进行位移加载;对柱底钢帽的底面进行固接。
2.4 模型的验证
为了验证有限元模型的合理性,本文将SRC、CFST、CTSRC和STSRC柱轴压试验进行数值模拟,其对比结果见表1。由表1可知,有限元和试验轴压承载力计算结果吻合较好,两者比值在0.94~1.11之间。由此可知,本文采用的有限元模型及材料本构是可靠的。
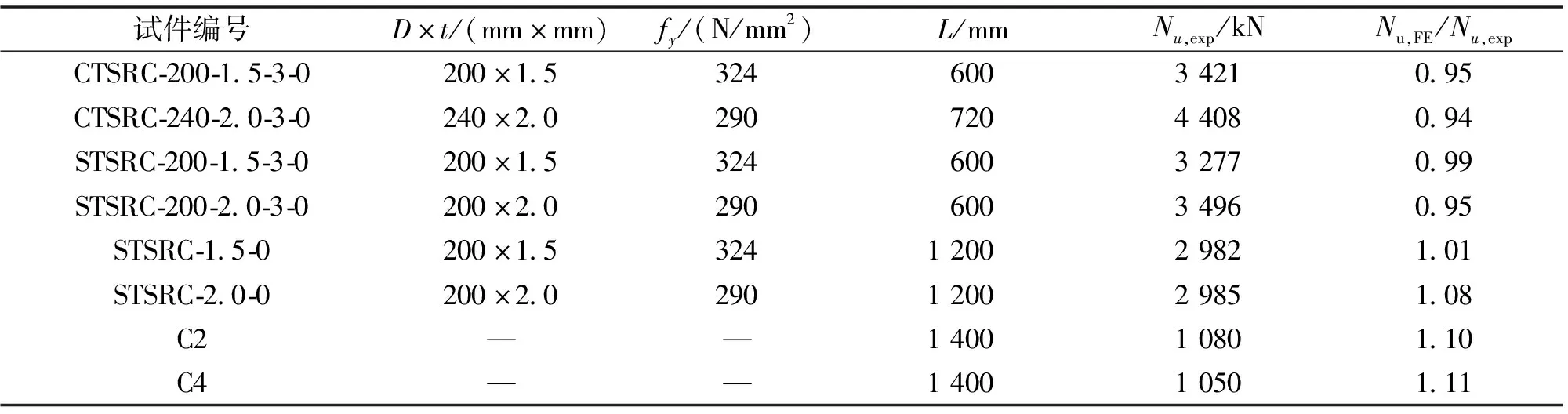
表1 试验和有限元极限承载力对比
3 有限元计算结果及分析
3.1 荷载-位移关系曲线
图5给出了各试件的荷载-位移关系对比曲线。从图中可以看出,4条曲线的变化趋势近乎一致,各试件模型在轴压下的受力特性可以分为:弹性阶段,弹塑性阶段以及破坏阶段。
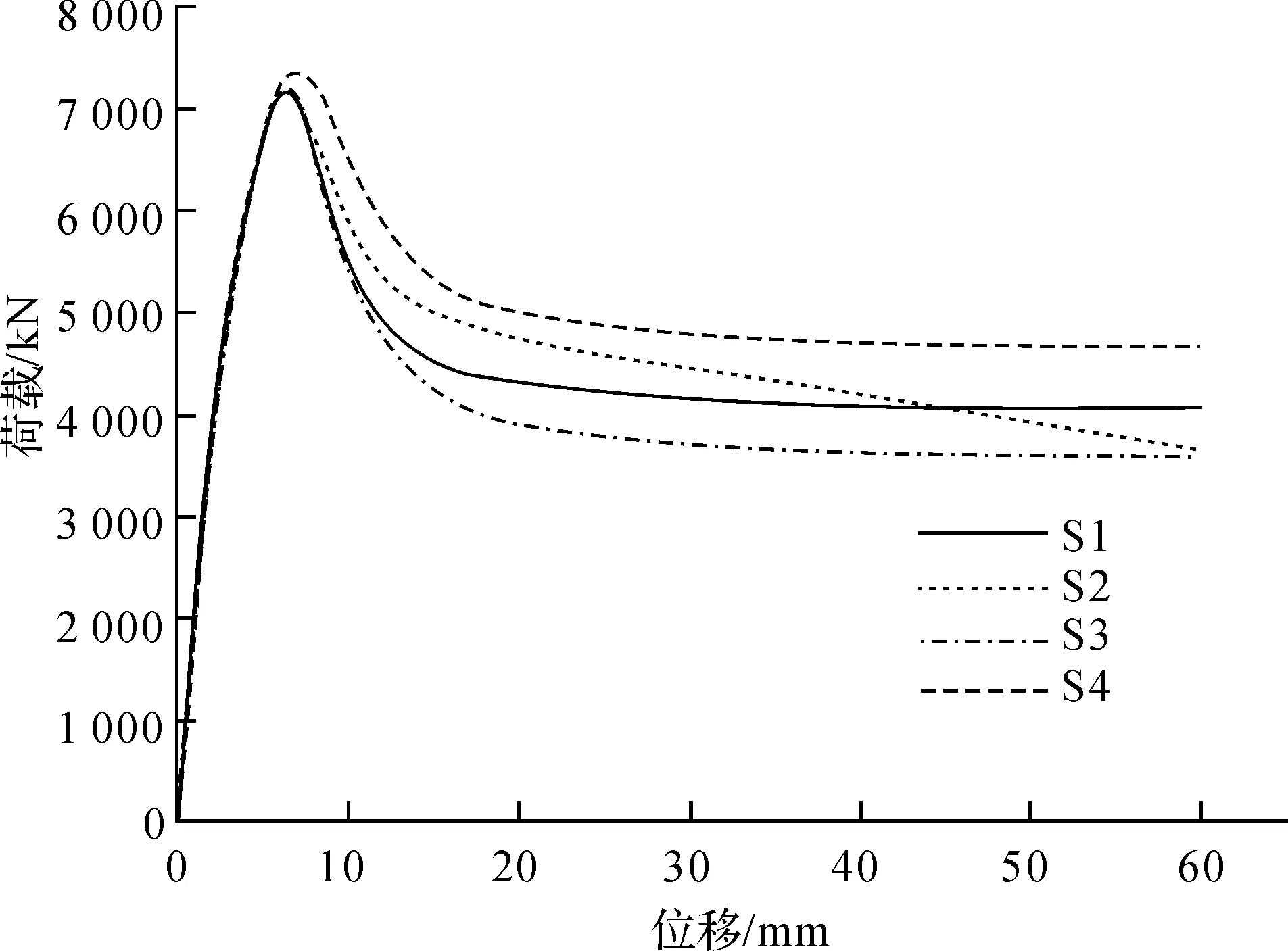
图5 S1~S4荷载-位移曲线
在弹性阶段,各试件模型均产生弹性变形,荷载-位移关系近乎是一条直线,S1~S4柱的初始刚度差别不大;随着位移的继续增大,试件模型进入弹塑性阶段,该阶段内型钢及钢管达到屈服强度,各试件的刚度均有所下降;当位移达到6.23 mm时,模型开始发生破坏,承载力下降,且内部构件含圆钢管的试件(S2、S4)在相同位移下承载力下降更为缓慢,延性更好。图6给出了各试件的最终破坏模态,由图6可知,内部型钢或外包钢管的截面为圆钢管的S2和S4柱对局部缺陷的敏感度更高,破坏时柱中向一侧屈曲;S1和S3柱最终发生传统轴压破坏形式,其破坏位置分别为柱中及柱两侧。
3.2 承载能力
图7给出了S1~S4试件柱的极限承载力对比曲线。从图7中可以看出,相比于S3柱,S2、S1以及S4柱的承载力分别增长了68.93、75.47 kN及185.99 kN,说明当含钢率相同时,CTSRC柱的轴压承载能力最强。这是由于外包圆钢管对内部混凝土的环向约束作用更强,从而增强了混凝土的抗压强度,提升了柱整体的承载力。
3.3 延性
延性系数作为判断结构性能的重要指标之一,是用于表征结构后期变形能力的重要参数。根据文献[6],用位移延性系数μ表示:
(2)
其中,Δu为承载力下降到峰值荷载85%对应的位移值,Δy为屈服荷载对应的位移。
由表2可以看出,相比于S4,S1~S3柱的延性系数分别降低了24.9%、20.8%以及26.3%,表明CTSRC柱在轴压作用下其塑性变形能力更强。此外,S2柱比S1柱的延性系数提升了5.1%,S4比S3柱的延性系数提升了22.4%,由此说明将型钢或外包钢做成圆钢管的形式可以改善构件的塑性变形,使其整体具有更好的延性。
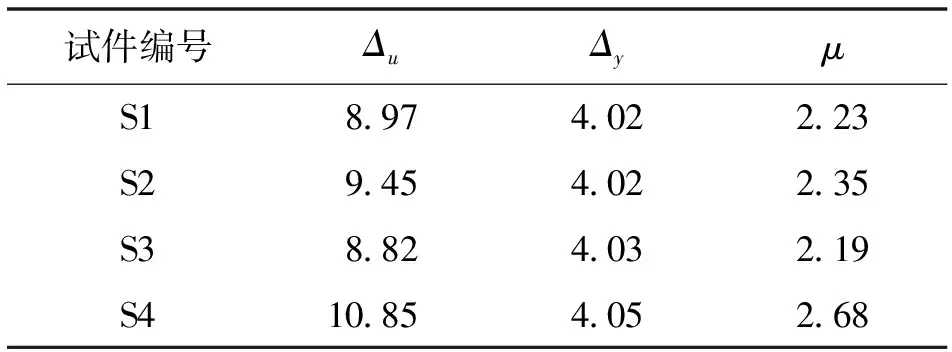
表2 各试件的屈服位移、极限位移以及延性系数
3.4 约束效应分析
图8给出了各试件轴向位移分别为3.45、6.23、9.01、12.7 mm时柱中部型钢对混凝土的约束效应对比图。图中横坐标为型钢跨中截面的应变率,由其横向应变与竖向应变的比值确定;纵坐标为沿跨中截面的应力分布位置。由图8可知,各试件型钢的约束效应随着位移的增大而提高,且在位移达到9.01 mm时提升最为明显。对于型钢为工字型的S1、S3及S4柱,翼缘和腹板连接处的约束效应强于腹板处,且随着位移加载,两者的约束效应逐渐趋于一致。此外,当位移为6.23 mm时,S1、S2中截面的平均应变率(0.563、0.559)大于S3和S4柱(0.465、0.497),表明SRC柱和CFST柱在极限承载力下内置型钢具有较强的约束作用。对比S1和S2柱可知,虽然SRC柱在6.23 mm时的约束效应略高,但CFST柱的约束作用分布更为均匀,更利于受力。极限荷载之后,S4柱的约束效应明显大于S3柱,这是由于圆钢管的约束区域大于方钢管,因而CTSRC柱中混凝土对型钢的挤压面积更大,型钢的约束效应更强。
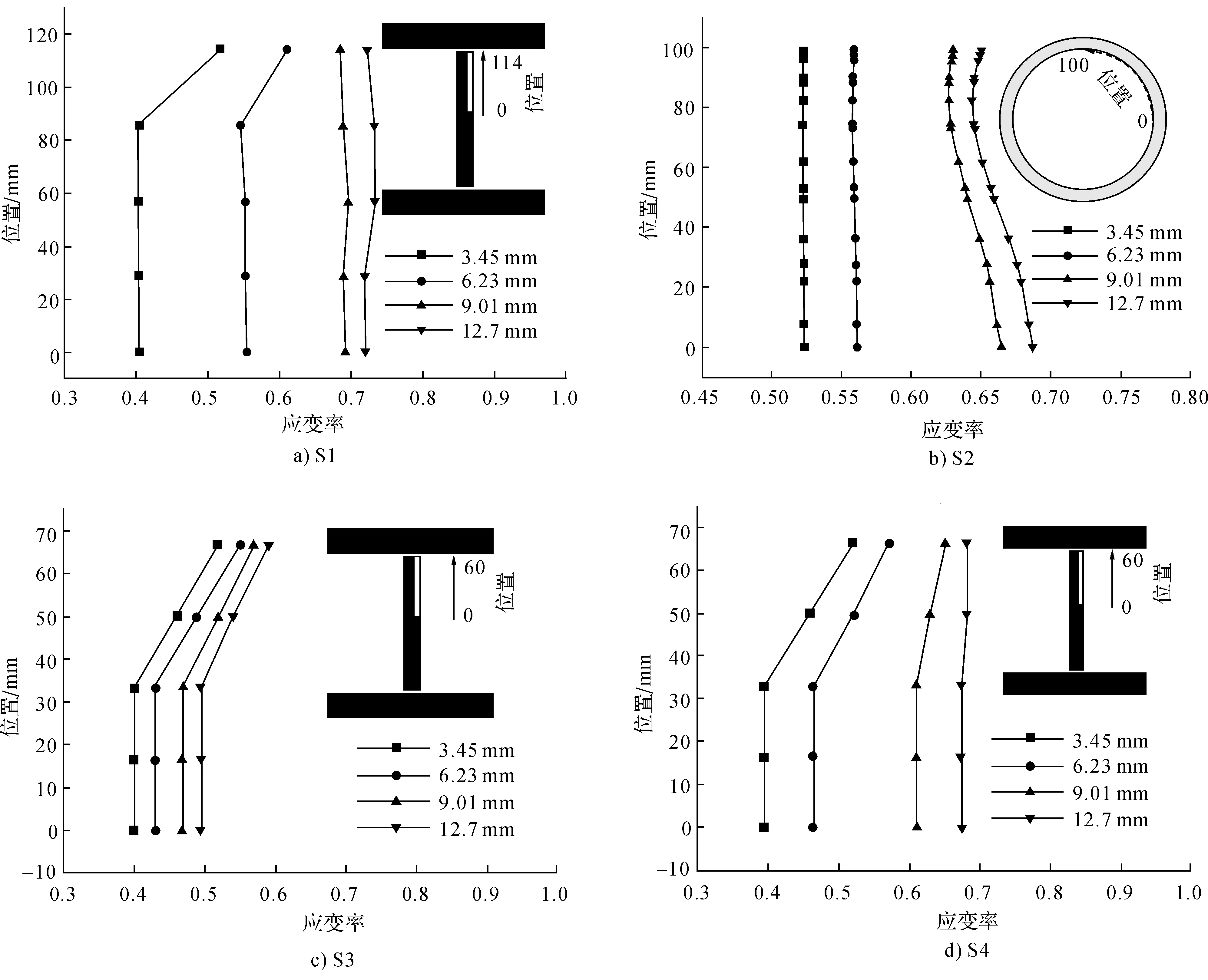
图8 S1~S4跨中位置的应变率分布
4 结 语
利用ABAQUS有限元软件对不同截面形式柱进行轴压力学性能分析,可以得到如下结论:
1)《混凝土结构设计规范(GB 50010—2010)》中推荐的混凝土本构关系可运用于ABAQUS有限元分析中,并且能较好地反映混凝土的受力特性。
2)各试件的荷载-位移曲线的变化趋势基本一致,且截面中包含圆钢管的CFST和CTSRC柱易于发生屈曲破坏。
3)在相同含钢率下,CTSRC柱的轴压承载力最强;对比四种截面柱,CTSRC柱的塑性变形能力最强,且在构件内嵌入圆钢管可有效提高其整体延性。
4)各试件内型钢约束效应随位移加载而增大,且从峰值位移至极限位移内增长最为显著。此外,在极限承载力下CFST柱内型钢的综合约束效应优于其余截面形式柱,并且峰值荷载后CTSRC柱的约束效应大于STSRC柱。

