定量相衬成像中自适应阈值翻转的相位解包裹算法

林盼明， 罗 都， 李 军， 黄佐华

(华南师范大学物理与电信工程学院， 广州 510006)

相衬法是常见的定量相位分布成像方法,在透明生物医学细胞显微成像、透明材料、微透镜检测、干涉计量、流场密度分布测量等领域有广泛应用[1]. 在全场的真实相位分布重构中，常常涉及相位的解包裹过程. 实际上，相位解包裹计算已被广泛应用于干涉合成孔径雷达、基于结构光的三维测量、光学干涉测量与成像等测量方法中[2-4]. 在从干涉图获取相位的过程中，一般要用反正切范数提取相位，致使连续的相位被截断，值域被限定在(-π,π]，形成包裹相位. 故需要对包裹相位进行解包裹，将截断相位重构，以求得真实的连续相位[5]. 但实际情况下，包裹相位由于欠采样、含有噪声、局部阴影等影响因素，常会出现残差点区域，影响解包裹的精度，给解包裹增加了难度[6]，也间接影响真实相位重构的精确度.

现有的相位解包裹算法众多[7-15]，主要有2种：路径跟踪算法和路径无关算法. 其中，路径跟踪算法主要有枝切法、质量图导向法和掩膜割线法等[16-18]；路径无关算法主要是寻求满足最小范数的解，如基于离散余弦变换的最小二乘法、基于快速傅里叶变换的最小二乘法等[19]. 严重欠采样和较强噪声对解包裹来说是两个难题，钱晓凡等[4]提出了横向剪切最小二乘法(LSBLS)，郭媛等[20]提出了四向横向剪切最小二乘法(FLSBLS). 这些算法可以恢复欠采样相位图，但仍然无法有效求解严重欠采样的包裹相位图.

近年来，自适应阈值在图像分割、去噪、去雾、相位转换等方面应用广泛. SERT等[21]基于结构光系统提出采用自适应阈值相位转换三级校准算法进行三维物体的测量. 在图像处理方面，有研究者提出基于自适应阈值移除背景的边缘投影轮廓测定法[22]，也有将自适应阈值用于细胞图像处理[23-24]及图像去噪声[25]等. 目前，自适应阈值在图像解包裹方面尚未被广泛应用.

针对常见解包裹方法存在的不足，本文提出一种基于自适应阈值翻转的相位解包裹算法(SATR). 对于包裹相位被截断的多峰模型，采用程序自动寻找最佳阈值，确定相位凹陷处的边界，得到一个只有凹陷处值的矩阵，再对该矩阵进行翻转操作，替换原矩阵中凹陷处的值，从而实现真实相位的还原. 通过程序自动寻找自适应阈值，能有效避免手动设置阈值，提供正确阈值选择，提高了相位还原的效率及准确性，有较强的抗干扰能力.

1 研究方法

1.1 相衬成像的基本原理

相衬成像的基本思想：在含有被测物体相位信息的物光波中，通过改变零频分量或高频分量的相位，将物光波的相位分布调制成可以观察的强度分布. 设样品为纯相位型物体，振幅为A的平行光正入射到物平面上，则物光场的复振幅可表示为：

f(x,y)=Aeiφ(x,y).

(1)

若忽略相干光学系统有限孔径的影响，其频谱为：

(2)

如果在频谱面上加泽尼克相板，其空间滤波函数为：

(3)

其中,t与φd分别为相板的振幅透过率与相移量. 加相板后，像面的光强分布数学表达式可写为[26]：

I=A2{t2+2[1-cosφ(x,y)-tcosφd+

tcos(φd-φ(x,y))]}.

(4)

要求解相位分布φ(x,y)，还需要知道不放置样品和相板时，像面本底光强度I0的大小. 考虑到对实际样品成像时，多次移动相板会增加许多无谓的工作量，因此在不移动相板的情况下，直接移开样品或让样品中不含物体信息的区域光场通过. 此时，像面本底光强度可表示为：

I0=A2t2.

(5)

由I(x,y)和I0可计算出被测样品的相位主值分布：

(6)

其中,B=(1+t2-2tcosφd)1/2，β=arctan(tsinφd/(tcosφd-1)). 根据式(6)可以确定0～π范围内的相位值，因此，当被测物体相位变化较小时，即其相位分布变化范围在0～π时，I(x,y)能直接反映物体的真实相位分布；如果物体相位超过π，拍摄2幅相衬图像(即本底光强图I0及相衬包裹干涉图I(x,y))，由于相位被包裹，不能直接求解，这就需要利用上述反余弦关系，通过解包裹才能重构被测相位物体的真实相位分布.

1.2 自适应阈值翻转相位解包裹算法

在自适应阈值翻转相位解包裹算法中，采用最佳阈值的方法确定包裹相位凹陷边界、找到凹陷范围并进行翻转操作. 基于翻转法的解包裹方法要求处理包裹相位分布中的包裹层叠部分，将其移到真实区间，因此，如何寻找凹陷、确定凹陷处的边界以及如何实现自动翻转是翻转算法解包裹的核心.

自适应阈值翻转算法的基本原理是通过寻找阈值(阈值设为W，0.9≤W≤1)作为获取凹陷边界的依据(此处共有11个阈值). 在提取包裹相位矩阵中，相位大于Wφmax像素并将该像素区域相位设置为1，其中φmax为输入相位矩阵的相位最大值，故标记为1的部分为凹陷部分，而其余像素设置为0；找到相位凹陷后，对包裹相位凹陷部分进行自动翻转替换；将翻转替换后的矩阵记为φ00，进行滤波平滑处理后将矩阵记为φ00T，保存并比较每一个阈值对应的φ00和φ00T的相对误差，找到最小误差对应的相位矩阵和阈值并输出，此时的阈值为最佳阈值，输出滤波平滑后的相位矩阵φ00T则为最佳解包裹相位分布. 自适应阈值翻转算法解包裹的程序框图如图1所示，其中，实现自动翻转替换算法的实现过程可用图2所示的程序框图来体现，其基本原理：对程序找到的只有凹陷处相位分布的矩阵进行判断. (1)若该矩阵为非零矩阵，则对该矩阵进行翻转，翻转后用得到的矩阵替代原相位矩阵φ00中凹陷处的位置，最后进行判断;(2)若该矩阵为零矩阵，则终止循环，输出所得到的经过翻转替代的矩阵φ00，否则将继续循环直到找不到凹陷为止. 另外，翻转的对称轴在第一次为π，第二次为2π，第三次为3π，以此类推.

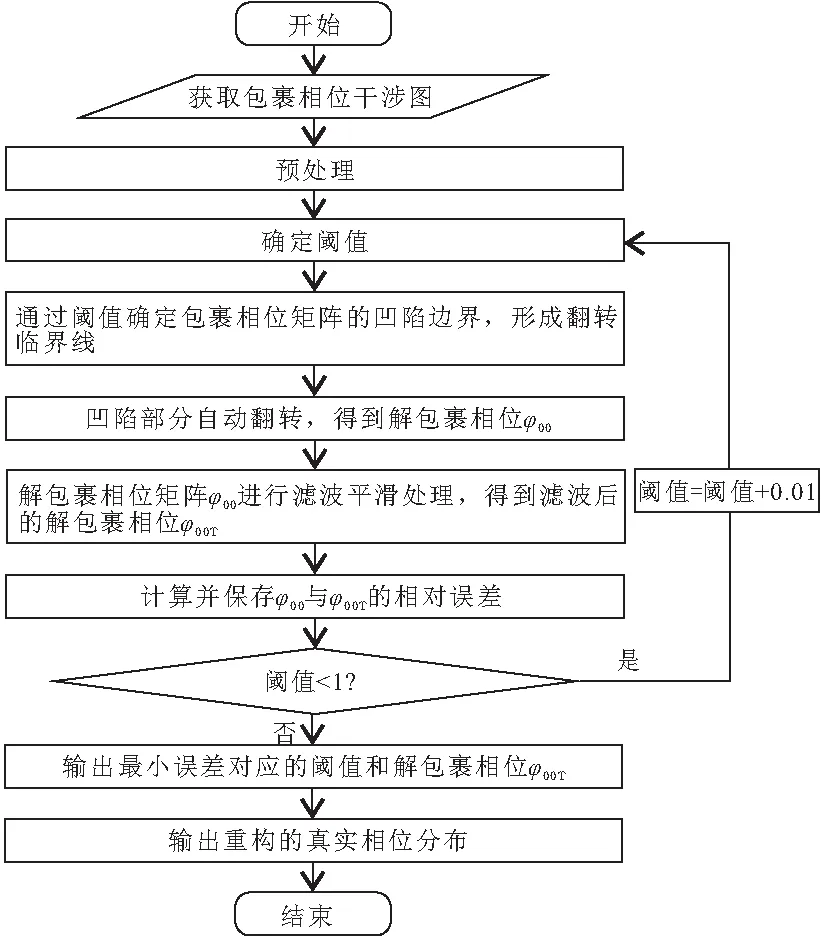
图1 自适应阈值翻转算法(SATR)解包裹的程序框图Figure 1 The block diagram of self-adaptive threshold reversal algorithm for phase unwrapping

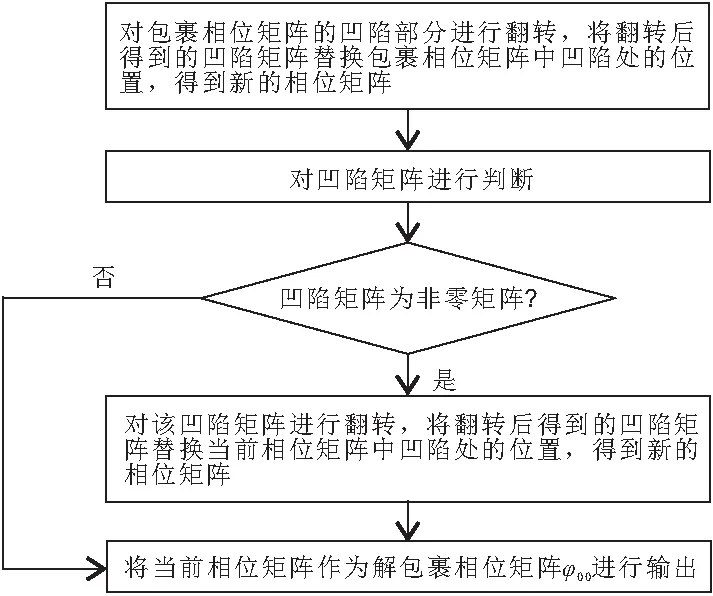
图2 自动翻转替换算法的程序框图Figure 2 The block diagram of automatic flip-to-replace algorithm

2 数值仿真结果

2.1 4种相位解包裹算法精度的比较

构建一个512 px×512 px且2倍峰值的原始相位分布，其最大相位为16.2 rad. 在不考虑噪声的条件下，分别采用LS、LSBLS以及FLSBLS与本文SATR算法对无噪声的二维包裹相位分布进行解包裹.

计算LS、LSBLS、FLSBLS和SATR算法的真实相位与解包裹得到相位的均方根误差(RMSE)分别为0.749 8、0.749 8、0.752 1和0.119 8 rad，本文SATR算法对相位恢复精确度明显高于其他3种算法，相对相位反演精度为99.26%. 算法使用凹陷相位翻转进行相位恢复，每次翻转替换得到的相位都由前一次翻转决定，而对下一次翻转无影响. 本算法通过设置程序寻找阈值W，将查找到的相位大于Wφmax像素作为凹陷部分，随后对相位凹陷部分进行自动翻转替换. 将翻转替换后的矩阵与经过滤波平滑处理后的矩阵作相对误差分析，找到最小误差对应的相位矩阵和阈值并输出，此时的阈值为最佳阈值，通过这种方法得到恢复相位的误差也较小.

2.2 抗噪性能比较

在实际应用中，图像都会存在一定的噪声. 在原始相位分布图像中加入不同程度的高斯噪声后，对512 px×512 px且2倍峰值的相位分布取绝对值，然后进行解包裹. 加入噪声后，先对原始相位进行滤波预处理. 解包裹后，要对恢复相位进行均值滤波处理，得到最终的重构相位分布. 表1为基于离散余弦变换的(DCT)最小二乘法与SATR算法解包裹的相位误差的性能比较. 图3是加入信噪比为3%的高斯噪声后得到上述2种方法解包裹的实验结果及比较.

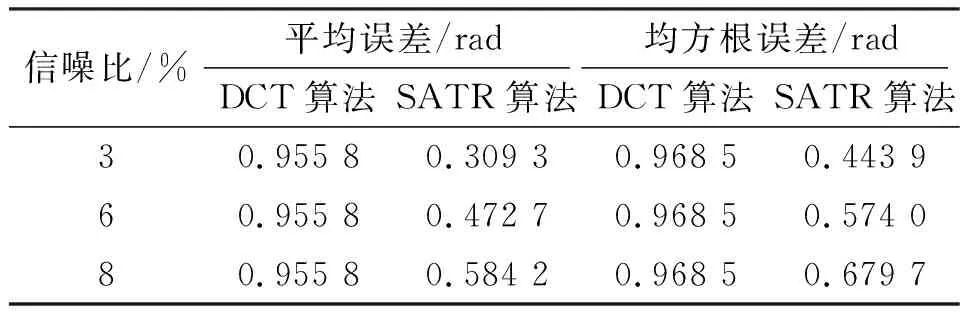
表1 2种相位解包裹算法的抗噪性能比较Table 1 The comparison of the anti-noise performance of two phase unwrapping algorithms

由表1和图3可以看出：对相位加噪声后，DCT解包裹的平均误差和均方根误差比SATR算法的都要大，SATR算法的解包裹精度优于DCT，相对相位反演精度为96.40%～98.10%；SATR算法的解包裹误差会随着噪声的增大而增大，但SATR算法的相位误差始终小于DCT的解包裹误差. 但总体上，大的噪声越大一定程度上会影响解包裹的结果. 通过以上对比可知，SATR算法可以在一定程度上减小噪声对相位解包裹的影响，提高了解包裹精度.

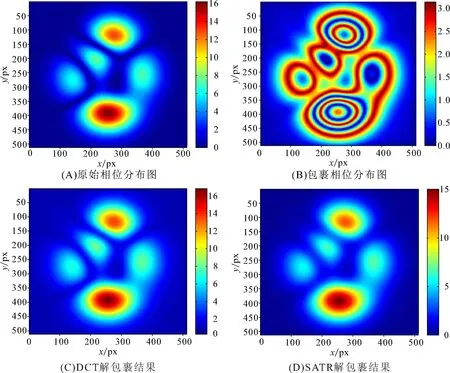
图3 含噪声包裹图的2种相位解包裹方法的结果比较Figure 3 The comparison of the results of two phase unwrapping methods for enveloping diagrams with noise

此外，实验还表明：经典的相位解包裹算法[27]由于迭代速度较慢而不适合网格大于64 px×64 px的相位解包裹运算，而提出的阈值翻转算法能够适合计算量较大、网格大小为1 501 px×1 501 px的相位解包裹运算，且解包裹精度可达96%.

3 实验验证

3.1 系统设置

为了验证SATR算法的实际应用效果，搭建基于相板调制的定量相衬成像实验光路(图4). 从半导体激光器(波长635 nm)发出的光束经可调衰减器NF、扩束镜、准直透镜形成平行光波照明样品，透镜L2和L3(焦距均为180 mm)组成4f系统对样品进行成像，在透镜L3的后焦面上产生相衬干涉图样. 在透镜L3的成像面上放置CCD数字摄像机(型号Guppy PRO F-125B，像元尺寸为3.75 μm)，对相衬干涉图像图样进行采集. 实验采用振幅透过率t为0.3、相移量为1.1π的自制相板.

图4 相衬成像实验光路Figure 4 The experimental optical path of phase contrast imaging

3.2 实验分析

选用微透镜阵列作为待测相位物体，其中单元微透镜球面的厚度约3.52 μm，用波长为635 nm的激光平行照射该微透镜阵列时，其球面顶部到底部的相位差约15.88 rad(5.055π).

实验系统像面上加相板后的光强分布如图5所示，图像噪声比较严重. 由图5A、B可分别得到微透镜的背景光强矩阵I0和相衬光强矩阵I，从而计算得到一个微透镜的包裹相位分布.

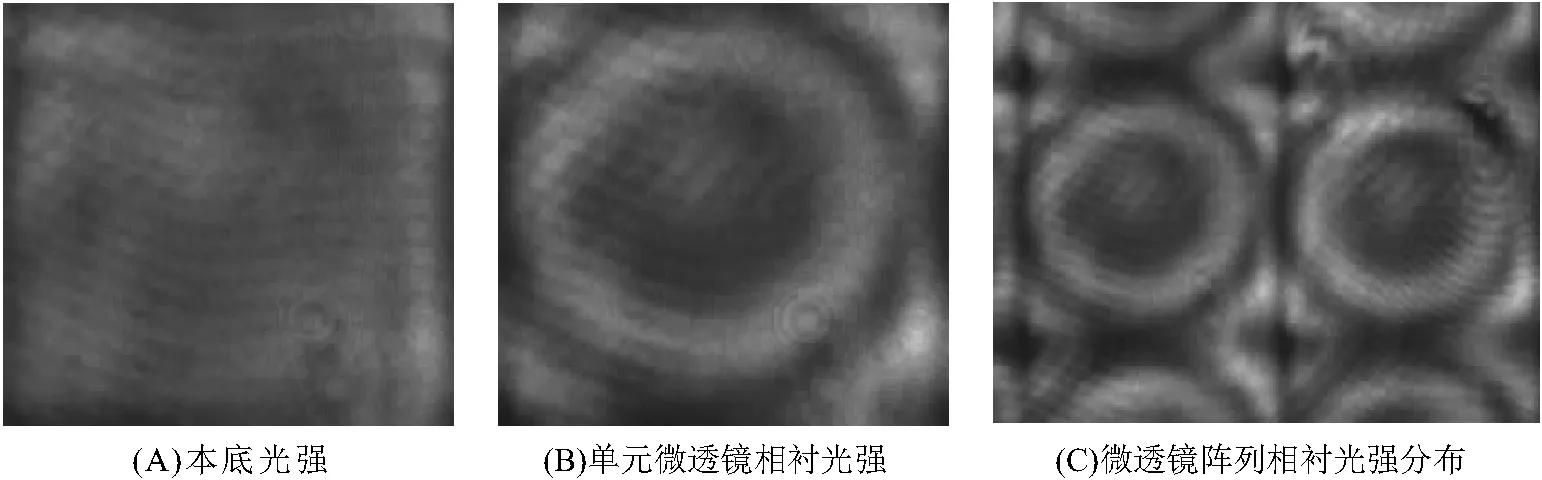
图5 微透镜阵列光强分布图Figure 5 The profile of micro lens array intensity

将微透镜的背景光强矩阵I0和相衬光强矩阵I代入反演公式(6)，得到二维包裹相位图(图6A)和三维包裹图(图6B)，在解包裹之前先将反余弦包裹转化为反正切包裹分布，再采用自适应阈值翻转解包裹算法对其进行处理，经过滤波后得到还原相位(图6C). 另采用横向剪切最小二乘法对其进行解包裹，经滤波处理后得到图6D. 通过对比图6C和D可知，这2种算法均可恢复被测物的基本相位分布，但SATR算法解包裹得到的重构相位分布更完整，LSBLS算法虽可以再现微透镜相位的大体轮廓，但由于误差传递的影响比较大，在峰顶出现了缺陷.

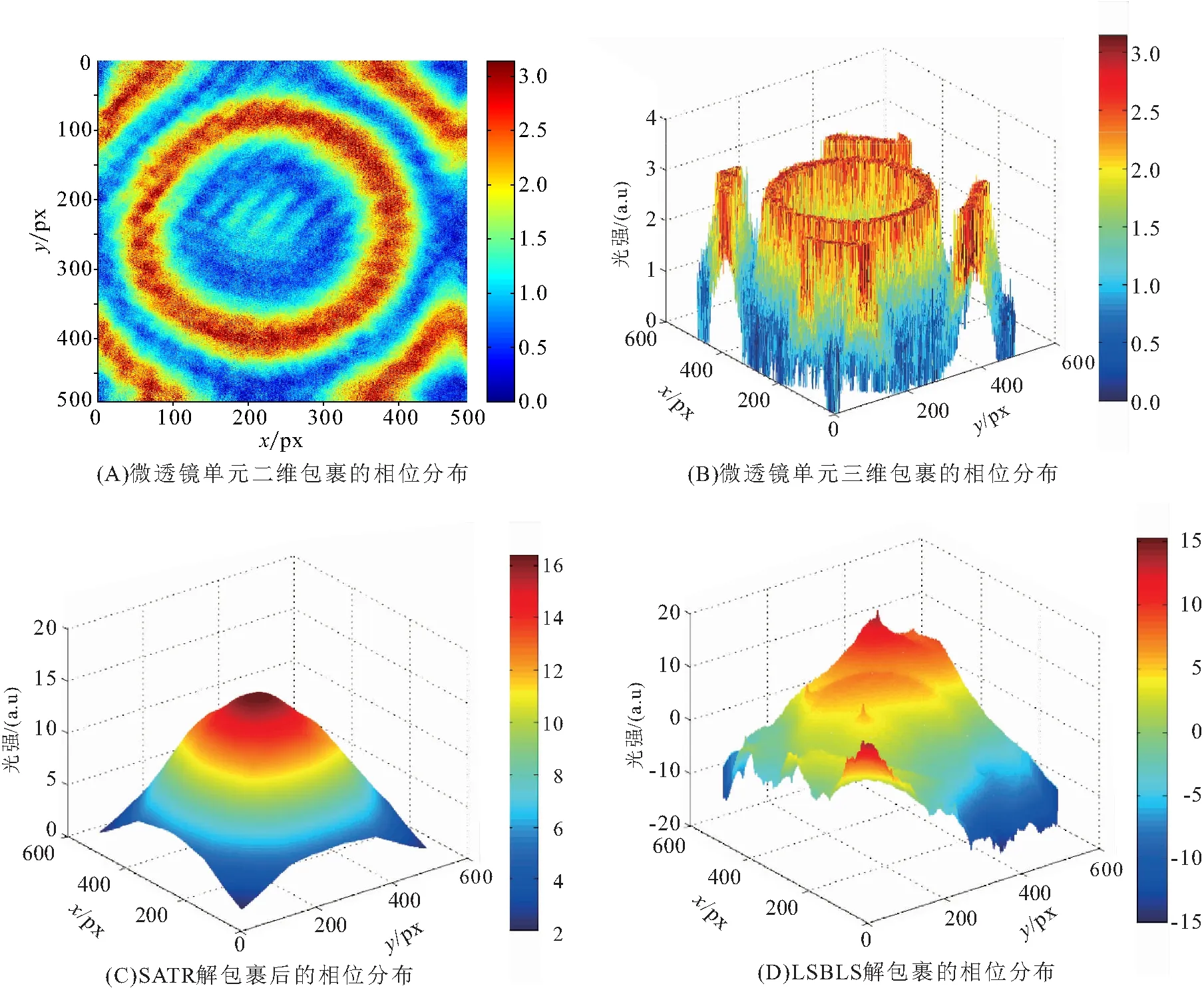
图6 SATR算法与LSBLS算法还原微透镜单元的结果对比Figure 6 The comparison of the results of reducting elements of micro lens between SATR and LSBLS

SATR反演得到单元微透镜的相位，其最大值约16.35 rad，厚度约3.62 μm，与微透镜阵列参数对比，存在约0.10 μm的绝对误差，相对误差为2.84%；LSBLS反演得到的单个微透镜的相位最大值约15.22 rad，厚度约3.37 μm，与微透镜阵列参数对比，存在约0.15 μm的绝对误差，相对误差为4.16%. 可见，SATR算法应用于微透镜单元解包裹得到的结果误差较小，能更好地还原包裹相位，其解包裹相位与原始相位基本保持一致，是一种可行且精确度高的实用算法.

4 结论

在相位解包裹中，自适应阈值相位翻转恢复相位方法最大的优点是利用自适应阈值确定相位翻转边界，能够以最小的相对误差求解出完整的真实相位，从而提高了相位解包裹的精确度. 通过与几种常见解包裹算法进行模拟计算和实验验证效果的对比，结果表明：该算法不仅可靠、抗干扰性强，而且适合于大计算量及任意相位周期的解包裹，具有应用价值.