编组站有中断服务的驼峰解体作业过程研究

林 枫，马 昆

LIN Feng1，MA Kun2

（1.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081；2.中国铁路北京局集团有限公司 衡水车务段，河北 衡水 053000)

(1.Transportation & Economics Research Institute， China Academy of Railway Sciences Corporation Limited， Beijing 100081， China； 2.Hengshui Car Depot， China Railway Beijing Group Co.， Ltd.， Hengshui 053000， Hebei， Beijing)

0 引言

编组站是铁路枢纽的核心，其主要任务是解体到达车列和按照出发去向编组新的出发车列，担负着有调和无调中转车的中转作业，素有“列车工厂”之称，是铁路运输系统中的重要组成部分。据统计，车列在技术站(主要是编组站)的作业与停留时间约占运输总时间的30%以上[1]，而车列解体需要的时间是在编组站内总停留时间的重要组成部分，因而研究驼峰解体车列的作业流程和特点，准确计算车列停留时间等作业指标值，对于优化车列在编组站作业效率至关重要[2-3]。

既有研究主要将解体系统模拟为M/M/1 排队系统，即到达流、服务时间等参数服从指数分布。毛保华[1]在模拟解体排队系统时，应用有中断M/M/1 与一般M/M/1 模型对比模拟编组站到解系统；针对单一服务员的排队系统，很多研究在求解时将随机变量设定为指数分布或一般分布，但是将其设定为爱尔朗分布的却很少。Wang，Huang 等[4-5]在考虑机器维修问题时应用M/En/1 排队系统，将维修机器的维修时间和服务员的中断时间假定为爱尔朗分布，服务员依据系统内停留顾客数来进行服务的中断或开始；Jain 等[6]研究单一服务员且服务时间服从爱尔朗分布的排队系统，当系统空闲时驼峰休息，当系统繁忙时驼峰有可能发生故障中断服务；林枫等[7]计算编组站分别采用定时、定编集结相关指标值，并对经济效益进行分析；Dorda 等[8]探讨有中断服务的单一有限服务排队系统，应用CNP tools 进行仿真模拟。

既有研究中，将驼峰解体时间设定为负指数分布与实际情况不相符，并且未考虑由于工作人员交接班、驼峰设备检修等作业导致驼峰作业中断的情况。根据陶德高等[9]对我国8 个主要编组站相关数据拟合可知，解体系统输入流服从指数分布，驼峰解体时间服从爱尔朗分布。考虑驼峰解体作业有中断的情况，基于排队论理论，将驼峰解体作业过程构建为到达流服从泊松分布、服务时间服从n阶爱尔朗分布且有服务中断情况的排队模型(以下简称“M/En/1”)，并采用仿真软件对求得的车列作业指标值进行验证。

1 编组站有中断服务的驼峰解体作业过程模型构建

1.1 解体作业过程排队

编组站解体系统的到达流是车列，出发流是车组，因而以车组为研究对象。车列进入到达场后即摘下牵引机车并进行技术检查作业，在到达线列检完毕的车列将作为输入流进入解体系统，考虑单溜放的驼峰作业方式，车列将形成解体系统中等待驼峰服务的队列，其中驼峰服务规则为先到先服务。

从排队论的角度，单一驼峰可以看作一个服务员，进入解体系统的车列可以看作按照去向需要驼峰解体服务的顾客。但是在驼峰服务期间，驼峰工作人员交接班、驼峰设备检修等作业将导致驼峰服务的中断。据统计，在正常情况下，驼峰至少要中断2 次/d，总时间在1 h 左右[9]。这种情况对车列占用驼峰的时间产生不良影响，延长车列的占线时间，应在计算时予以考虑。

1.2 有中断服务的 M/En/1 排队模型

1.2.1 驼峰作业过程状态转移关系描述

当采用有中断服务的M/En/1 排队模型描述驼峰对车列的作业过程时，将系统的工作状态用变量组合进行描述。根据驼峰3 个不同作业状态，将驼峰作业过程分成3 个工作状态集合，分别定义为子集Ω1，Ω2，Ω3，总集合Ω=Ω1∪Ω2∪Ω3。其中Ω1表示驼峰处于工作时的状态集合，Ω2表示驼峰即将中断作业时的状态集合，Ω3表示驼峰完成车列解体后系统中断作业，分别可以表示为

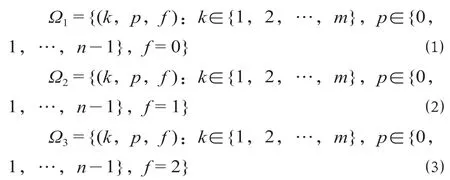
式中：k为系统内车列数；m为系统内股道数，因而系统内到达车列数不能超过m列，由于车列进行解体作业时需要占用一条股道，因而系统内等待解体的车列最多占用m- 1 条到达线；p为驼峰解体时已完成的解体步骤；n表示驼峰解体作业时间服从n阶爱尔朗分布(n≥ 2)，可以认为驼峰解体过程为n个串联服务窗，且每个服务窗的服务时间服从参数为nμ的n阶爱尔朗分布；μ为单阶爱尔朗分布参数，因而驼峰平均服务时间为n/nμ= 1/μ；f为驼峰解体状态参数，f= 0 表示驼峰处于工作状态，f= 1 表示驼峰正在解体车列，需要等待作业结束后中断服务，f= 2 表示驼峰完成车列解体后，中断作业。

在解体系统内，根据驼峰的3 个不同作业状态，构建驼峰作业状态转移关系图如图1 所示。根据图1 建立有中断服务的M/En/1 排队模型。图1中椭圆形表示驼峰的作业状态；P(k，p，f)表示作业状态(k，p，f)的发生概率；连接线表示状态转移方向。

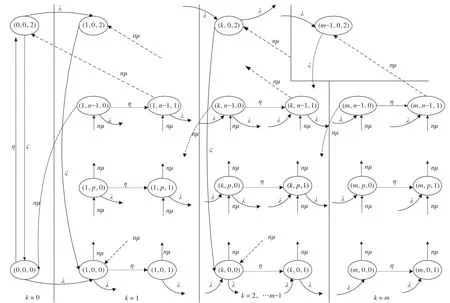
图1 驼峰作业状态转移关系图Fig.1 Hump operation state transition diagram

1.2.2 “有中断服务的M/En/1”排队模型

由图1 可知，当排队系统达到状态平衡时，每个状态概率都与其他状态存在关联关系，因而需对每个状态建立状态关系转移方程式。根据驼峰作业状态及系统内车列数的不同，分别从驼峰处于解体作业状态且未作业时(p= 0，f= 0)，驼峰即将中断作业且未作业时(p= 0，f= 1)，驼峰处于作业状态且已完成p作业步骤时(p= {1，2，…，n- 1}，f= 0)，驼峰即将中断作业且已完成p作业步骤时(p= {1，2，…，n- 1}，f= 1)，驼峰中断作业且未作业时(p= 0，f= 2) 5 个方面建立方程式。在上述5 种驼峰作业状态下，不同驼峰作业状态下k的分组是根据车列在解体系统内的状态转移关系是否相同来划定。当状态转移关系相同时则划为一组，否则分为不同组，从而得到驼峰作业状态转移方程式如表1 所示。

驼峰作业过程内所有状态概率之和为1，可以表示为

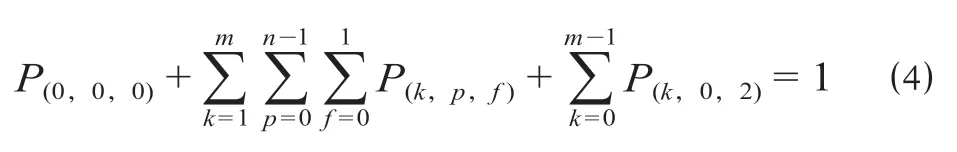
1.3 模型求解

采用 矩阵关系式进行求解。由于状态概率为三维数组，首先将三维数组转化为一维数组，然后应用求解所有的状态概率值，然后计算驼峰解体车列数、等待解体的车列数、车列总数、每列车在解体系统内的停留时间、每列车在解体系统内的等待时间5 个作业参数值。

表1 驼峰作业状态转移方程式Tab.1 Hump operation state transition diagram

（1）解体车列数。解体车列数计算公式为

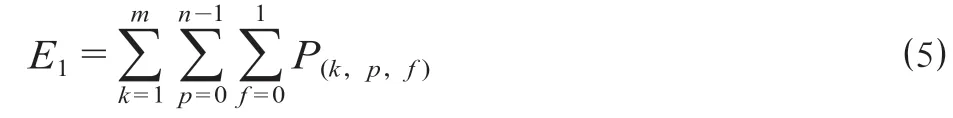
式中：E1表示解体系统内正在解体的车列数，列/min。

（2）等待解体的车列数。等待解体车列数计算公式为

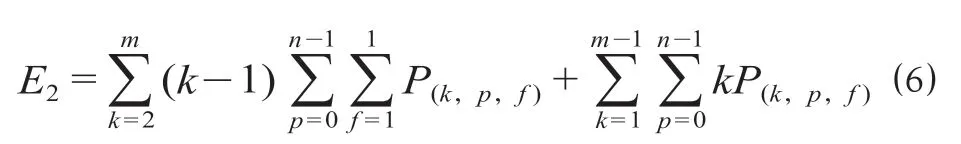
式中：E2表示解体系统内等待解体的车列数，列/min。

（3）车列总数。车列总数计算公式为

式中：E3表示解体系统内车列总数，列/min。

（4）每列车的停留时间。每列车的停留时间计算公式为

式中：T1表示每列车在解体系统内的停留时间，min，λ效表示有效到达流，即实际进入解体系统的平均车列数，列/min。

（5）每列车的等待时间。每列车的等待时间计算公式为

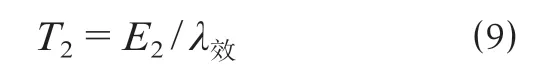
式中：T2表示每列车在解体系统内的等待时间，min。

2 算例分析

以编组站R作为实例来验证编组站驼峰解体系统模型。根据该编组站内驼峰作业特点，分别计算驼峰作业时间、中断时间、中断间隔时间，以及到达流的分布参数，然后将参数带入有中断服务的M/En/1 排队论模型内，计算车列在系统内的作业指标值；然后应用基于有色Petri 网的仿真软件对结果进行仿真，对排队论方法和仿真方法求得的2 组结果进行对比，验证排队论方法所得结果是否落在仿真方法所得结果的置信区间内。

2.1 参数计算

编组站R驼峰解体系统采用单溜放的驼峰解体方式，到达场有6 条到达线，车列等待空间为5 条股道。应用概率统计法得出到达流服从参数λ的指数分布、驼峰作业时间服从参数为nμ的n阶爱尔朗分布，计算得到单位时间内，实际进入解体系统的平均车列数参数λ效为0.035 2 列/min；单阶爱尔朗分布参数μ为0.049 6 列/min；驼峰中断间隔时间分布参数η为0.002 84 列/min；驼峰中断时间分布参数ς为0.03 列/min；到达股道数为6 条；驼峰作业时间服从8 阶爱尔朗分布。

（1）驼峰中断间隔时间分布参数。由于驼峰作业每昼夜中断4 次，中断总时间在2 h，因而驼峰中断间隔时间分布参数计算公式为式中：N中表示一昼夜驼峰中断次数；t中表示驼峰中断间隔时间，min。

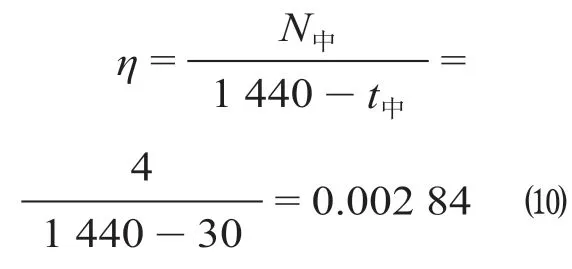
（2）驼峰中断时间分布参数。驼峰每次中断时间服从一般分布，中断时间分布参数计算公式为

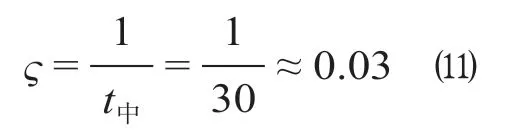
（3）车列有效到达强度。由于研究的是有限排队系统，即到达股道为m条，若到达场满员时，则不允许接车，此时车列到达强度为零，因而需要求出车列有效到达强度λ效，计算公式为

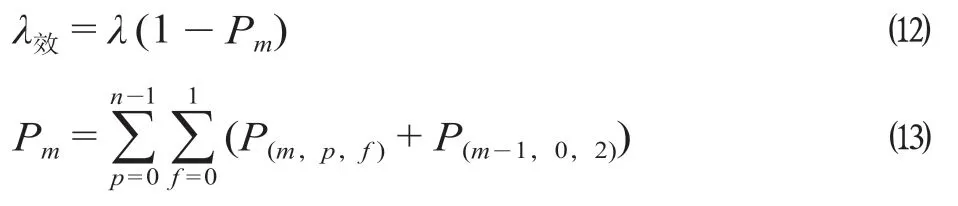
式中：λ效表示单位时间内，实际进入解体系统的平均车列数，列/min；Pm表示到达系统损失车列的概率。

2.2 仿真模型验证

应用仿真软件建立基于有色Petri 网的排队系统仿真模型，设置仿真次数为30 次，每次仿真时间为10 min，对车列在解体系统排队过程进行仿真，采用“有中断服务的M/En/1”排队论方法验证车列作业过程的可行性。基于有色Petri 网的排队系统仿真模型如图2 所示。图2 中椭圆形表示状态，矩形表示状态改变。

驼峰解体车列仿真过程主要分为车列进入解体系统和驼峰作业状态判断2 个环节，具体流程如下。

（1）车列进入解体系统。①系统初始化后，当且仅当排队系统内有空余的股道，车列可以进入解体系统排队等待，当系统内无车列作业，需要转入步骤（2）来判断驼峰是否可以进行解体作业；当系统内有车列进行作业，需要排队等待解体作业；②若系统内无空余股道，车列将不容许进入。

（2）驼峰作业状态判断。①当车列进入解体系统后，驼峰处于可解体状态时，等待车列进行解体作业，驼峰作业时间服从爱尔朗分布。②当车列进入解体系统后，驼峰处于即将中断作业时，若系统内有车列正在进行解体作业，需等待作业结束后驼峰中断作业；若无车列作业，则驼峰立刻进入作业中断状态，其中驼峰中断作业时间服从指数分布。

2.3 计算结果比较分析

当采用 矩阵关系式进行排队论模型时，由于状态概率为三维数组，首先将三维数组转化为一维数组，然后应用矩阵关系式求解，得到驼峰作业状态概率值如表2 所示。

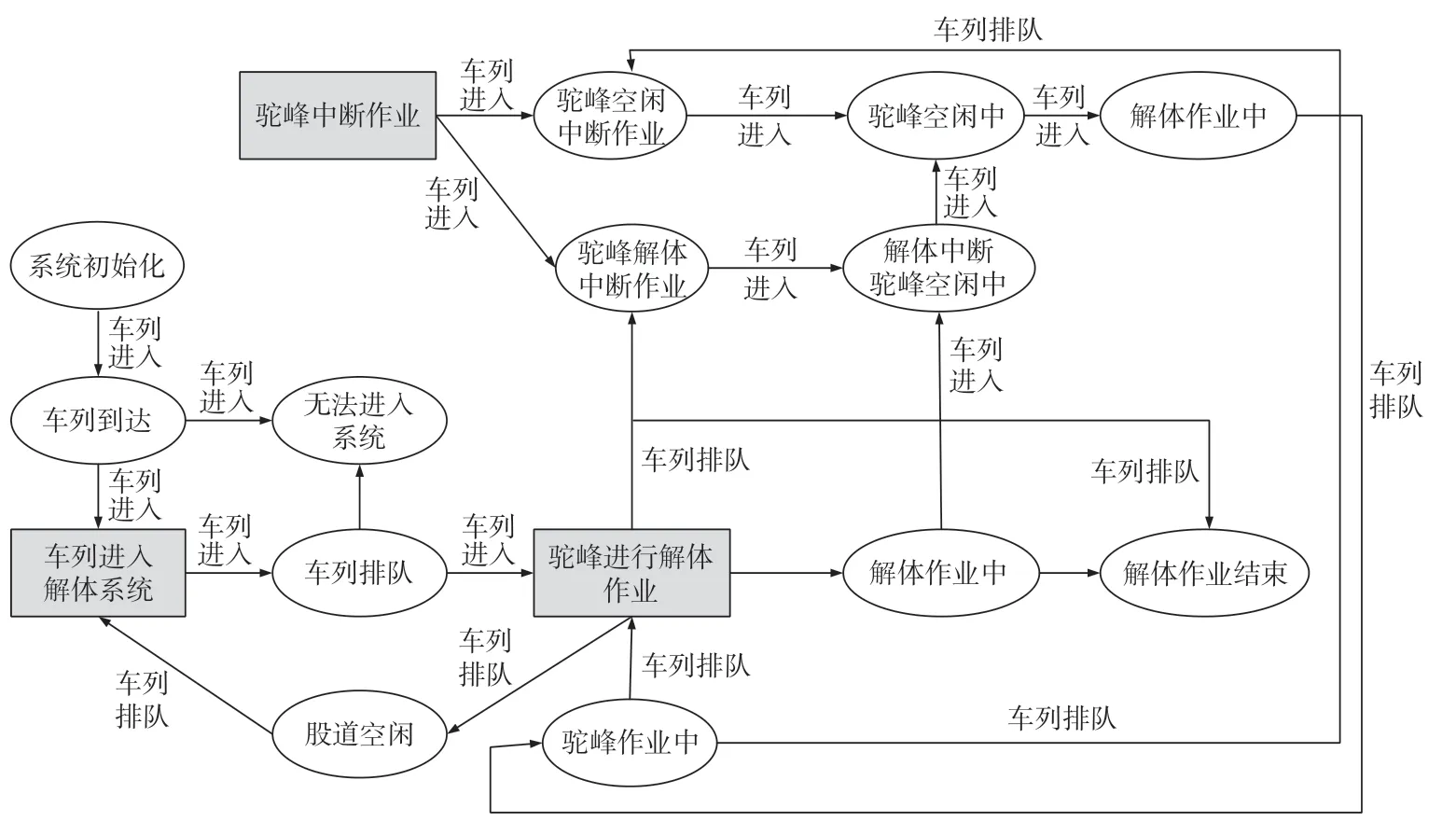
图2 基于有色Petri 网的排队系统仿真模型Fig.2 Simulation model of queuing system based on colored Petri nets

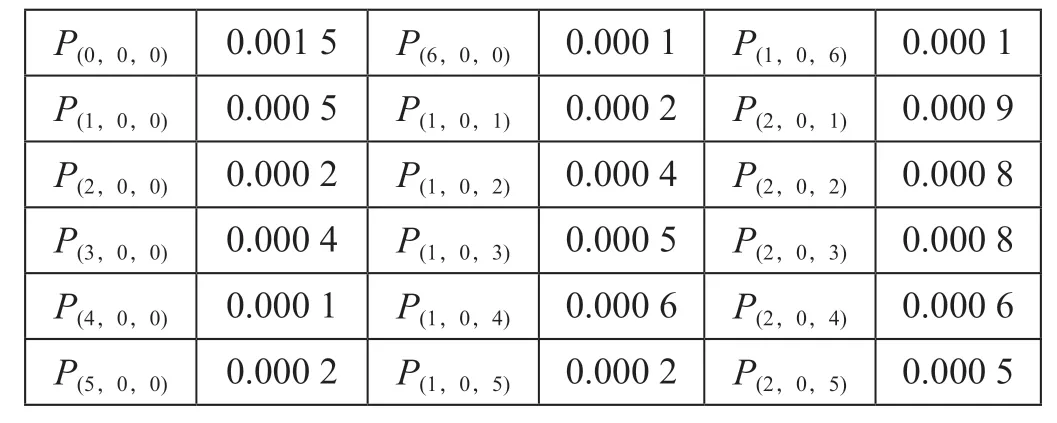
表2 驼峰作业状态概率值Tab.2 Hump operation state probability value

根据表2 中状态概率值，采用有中断服务的M/En/1 排队论模型和基于有色Petri 网的排队系统仿真模型，计算得到车列在解体系统内作业参数值如表3 所示。

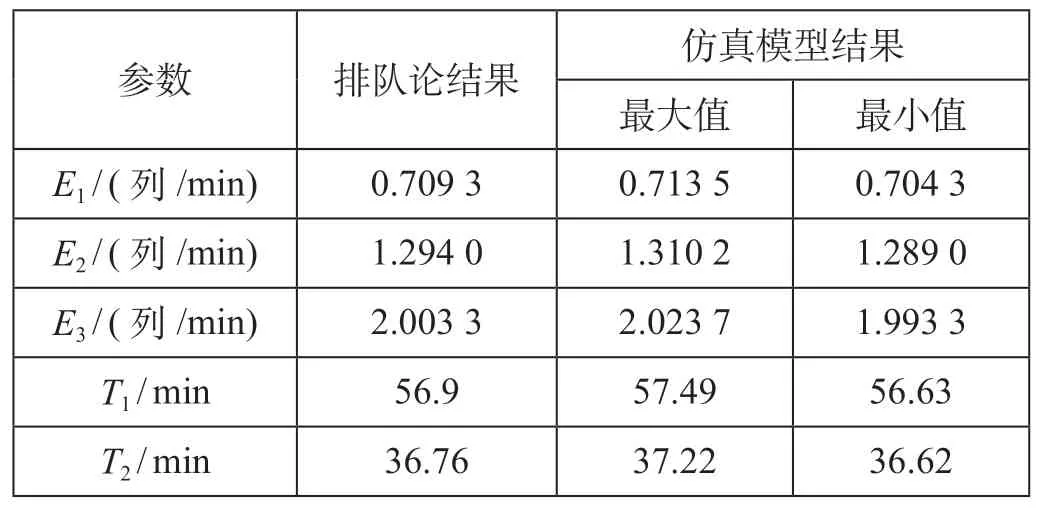
表3 车列在解体系统内作业参数值Tab.3 Operating index values of trains in the break-up system

由表3 可以看出，排队论得出的结果正好落在仿真结果的范围内，且与仿真结果的最大、最小值的差值在95%的置信区间内，说明应用M/En/1排队模型描述驼峰有中断服务的解体作业过程能够得到较为正确的结果，其中车列在解体系统内平均停留时间为56.9 min 与实际情况基本符合。

3 结束语

编组站作为铁路枢纽的核心，研究驼峰解体作业规律对提高车列在编组站作业效率，提升铁路在运输市场的竞争力至关重要。通过采用2 种方法对车列在驼峰解体过程中的作业指标值进行求解，得出应用“有中断服务的M/En/1”排队论方法构建驼峰有中断服务的解体作业过程具有一定的创新性，为研究车列的作业规律、分析不同因素对驼峰作业效率的影响奠定了理论基础；以作业指标值计算公式直接计算不同编组站内车列在驼峰解体过程中的指标值，从而为提高车列在编组站作业效率、促进铁路服务水平提升、满足客户对运输时效性的要求提供了理论支撑。