基于MATLAB 的二级倒立摆的稳摆控制研究

马 杰 张景钰

（陕西工业职业技术学院 机械工程学院，陕西 咸阳712000）

1 概述

倒立摆系统在控制学科是一个非线性、不易控制、阶次高、变量较多、变量之间关联性较强且稳定性较差的系统，从19 世纪中期开始, 倒立摆系统就常被用于控制领域的研究[1-3]。在控制学科中，一些不易理解的概念，都可以通过倒立摆摆杆的控制展现出来[4,5]。除了在理论上的应用，对倒立摆摆杆控制算法研究还可迁移到对行走机器人平衡性的控制、发射火箭时其竖直度的掌控以及其他的常见的工业控制领域都可通过对倒立摆的控制进行研究[4,5]。因此从理论和实际来看，对倒立摆的研究有着重要意义[6,7]。国内外对于直线一级倒立摆或环形一级倒立摆的研究较多，相对而言，对于二级倒立摆的研究就相对冷淡，同一级摆的控制相比，二级摆的控制更加复杂多变。与一级摆相同，环形二级倒立摆的控制研究也分为两部分：将摆杆甩起的控制及在竖直向上位置的稳定控制。作为欠驱动系统，二级摆的稳摆控制是通过电机直接驱动与之连接的水平连杆，带动与之相连的垂直面内的中间连杆，从而控制连在中间连杆末端的摆杆垂直稳定在竖直向上的位置[8]。本文主要是针对环形二级倒立摆的摆杆稳定控制问题进行研究，通过对二级倒立摆建立数学模型后，借助MATLAB 平台加入LQR 控制器进行仿真，通过固高环形二级倒立摆实时控制台进行实验验证，分析LQR 控制器应用于环形二级倒立摆的控制效果。

2 系统建模

针对实验室现有倒立摆试验系统，抓住建模主要影响因素，在假设的情况下，把环形二级倒立摆简化成由一个水平杆、两个竖直方向的摆杆以及连接各独立部件的两个质量块组成的系统。不同于以往二级摆简化建模，此处考虑到编码器及连接质量块的重心问题，使所建模型更贴近实物，其对应各具体参数如表1。

将实验室具体的倒立摆实物进行数学建模分析，对其系统建立图1 的所示的简化建模分析图，以便对研究对象进行模型的搭建。

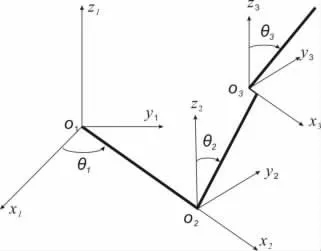
图1 环形二级倒立摆建模分析图

表1 数学建模物理参数

此处通过常用的拉格朗日方程对研究对象进行数学模型的搭建分析。在此研究对象中，系统的广义坐标为：

2.1 研究对象系统动能

在环形二级摆系统当中，系统动能主要涉及五部分：水平及竖直方向上的连杆（共3 个杆件）、用于测量竖直中间杆角度的编码器及用于测量上摆杆角度的编码器2 这五个部分的能量，其计算公式如下：

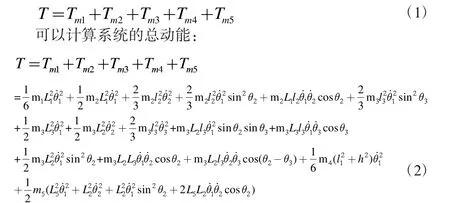
2.2 研究对象系统势能

计算中选择水平杆中心所在面为研究系统参照的基准势能面，那么系统的总势能主要有：编码器1、竖直中间杆、编码器2及竖直上摆杆这四部分的能量，表达式如下：

则系统总势能：

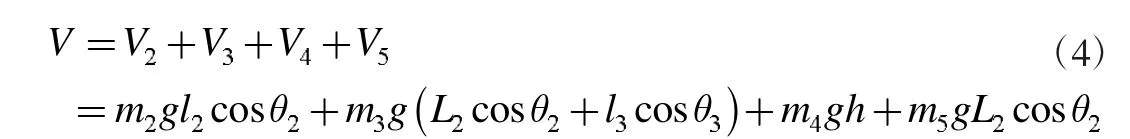
2.3 系统动力学方程

根据拉格朗日方程有：

3 控制器设计

本文选取LQR 进行二级摆的控制仿真实验。LQR 算法是现代控制理论里一种最优调节控制器，其发展较早现在也较为成熟。LQR 控制通过一个线性控制算法，表达如下：

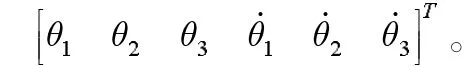
图2 MATLAB 中仿真曲线图

4 实验验证及结论

从图3 实验曲线可以看到，控制刚启动时外在初始条件对杆件角度影响较大，但不影响实验结果，可以看到中间杆和上摆杆都在2s 内稳定于平衡位置附近，整体与仿真结果一致。从仿真和实验结果验证了LQR 控制算法可以较好地用于环形二级倒立摆的控制。

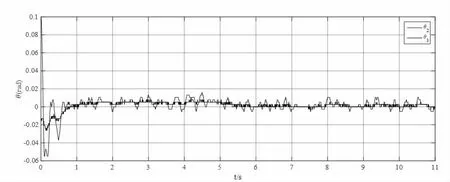
图3 二级摆LQR 实验结果