GAMS 在复杂系统中的应用研究

马书艳

（华北电力大学，北京102206）

GAMS（General Algebraic Modeling System）是一款建模系统，是20 世纪开发出来旨在解决复杂模型、复杂数学规划问题的软件。

1 GAMS 的介绍

1.1 GAMS 的模型结构和分类

GAMS 程序结构主要由5 部分组成，包括集合、数据、模型、求解和报告[1]。其中集合主要作用是声明变量，通俗的说就是给变量起名字，表示相关量之间的逻辑关系，在使用中需要用到几个变量就用set 引导进行声明，一般用i,j 表示，是最基本的部分。数据包含参数、变量、标量和表格。未知的数用变量表示，已知的值用参数或者标量表示，标量一般指系数。接下来就是模型的建立，在GAMS 中，建立模型首先要声明方程，然后对模型进行声明，包括是线性模型或非线性模型等。之后就是求解语句，求解语句应solve 引导，是对上述建立好的模型进行结果的求解，用display 引导结果的输出，即形成报告。以上就是GAMS一个完整的模型建立和求解的过程，为了更直观的表示，如图1。

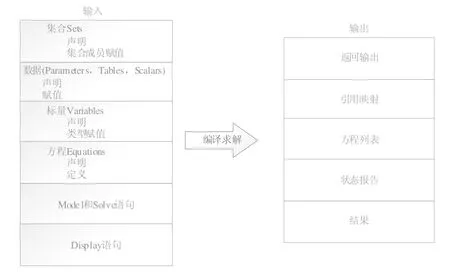
图1 GAMS 的模型构成

常见模型类型有:LP, NLP, QLP, DNLP, RMIP, MIP,RMINLP, RMIQCP, MIQCP, MINLP, MPEC, MCP, CNS[2]，对应的含义如图2。

1.2 GAMS 的求解器介绍

GAMS 有多种求解器可以调用，每种求解器的使用场景以及可使用的模型各有不同。下面介绍几种常用的求解器。（1）Branch-And-Reduce Optimization Navigator（分枝减小最优化导航，简称BARON），主要用于求解NLP 和MINLP 规划模型。使用加强分枝定界类型的算法，得到结果的最优。（2）MINOS 求解器：主要用于求解NLP 模型以及与NLP 模型相关的模型，并且所求模型的非线性函数必须是光滑的，即具有一阶导数，并且MINOS 求解器在解决上述相关类型函数时容易陷入局部最优，结果得到局部最优解而非全局最优解，这种情况下，选择一个合适的初始点，可以增加找到全局最优解的机会。（3）Cplex 求解器：特点是会针对特定的问题能够自动计算，为选项设置最优值。主要应用求解线性规划、二次约束规划和混合整数规划。（4）CONOPT 求解器：多方法求解器，和其他求解器使用方法类似[3]。

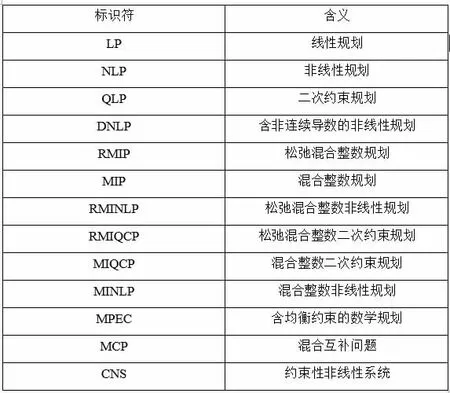
图2 模型类型标识符及对应的含义

2 GAMS 环境下的算例仿真

2.1 算例1：求下列复杂函数的最大值

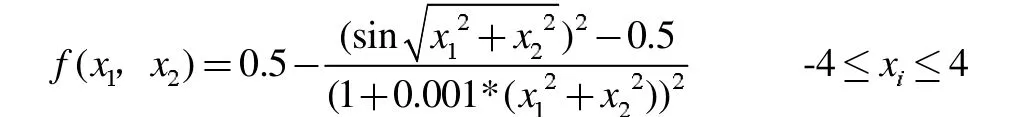
首先利用MATLAB 软件绘制测试函数图形，图形如图3：

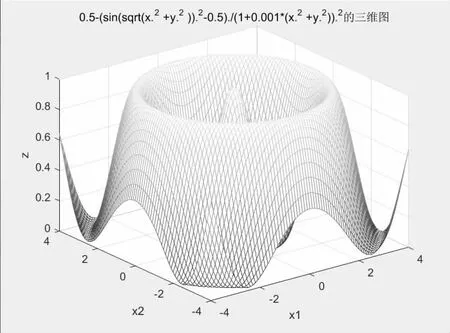
图3 测试函数1 图像

在GAMS 环境下对函数进行寻优，求出最大值。程序如下：variables

s 变量1

t 变量2

f 函数值；

equation fangcheng1 测试方程；

fangcheng1..f=e=0.5- {（sin （sqrt （s**2+t**2））**2-0.5）/（1+0.001*（s**2+t**2））**2}；

mode1 xunyou /all/；s.up=-4；s.10=4；t.up=-4；t.1o=4；s.l=0.1;t.l=0.1;

option nlp=baron; solve xunyou using nlp maxmizing f；display f.l；

仿真结果得出最大值为1。

2.2 算例2：求下列复杂函数的最值

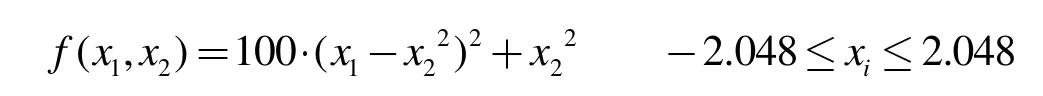
图4 测试函数2 图像

函数图像如图4。在GAMS 环境下进行最值的求解，程序如下：

variables

m 变量1

t 变量2

f min 最小值

fmax 最大值；

equation

fangcheng1 测试方程

fangcheng2；

fangcheng1..f_max=e=100*（t-m**2）**2+m**2；

fangcheng2..f_min=e=100*（t-m**2）**2+m**2；

mode1 xunyou1/fangcheng1/；

m.up=2.048；m.1o=-2.048；t.up=2.048；t.1o=-2.048；t.1=0.1；m.1=0.1；

option nlp=baron; solve xunyoul using nlp maxmizing f max;

mode1xunyou2/fangcheng2/;

m. up=2.048;m.1o=-2.048;t. up=2.048;t. lo=-2.048; t.1=0.1;m.1=0.1;

option nlp=baron; solve xunyou2 using nlp minmizing f min;

display f_min.1,f_max.1;

仿真结果得出最小值为0，最大值为3900.83。

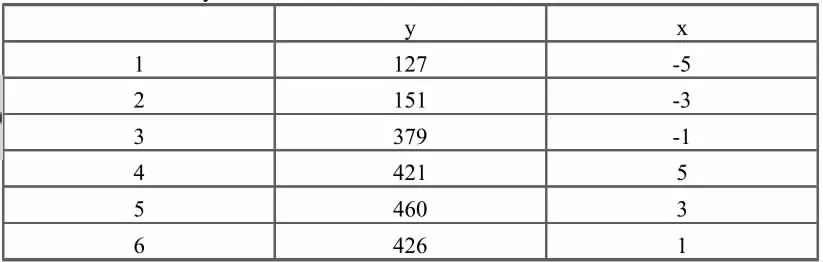
2.3 算例3：已知有关变量x 与y 的6 个样本观察点：

假设这六个样本点的曲线方程为：

Y=b1+b2*exp(b3*x)

求应用最小二乘法估计参数b1、b2 和b3 的值，使得曲线拟合误差最小。

?

GAMS 程序如下：

图5 算例3 程序

输 出 b1,b2,b3 和 Y 的 值 是：516.651，-149.352，-0.207,14085.14。

3 结论

GAMS 语言更适合解决大规模的、比较复杂的数学规划问题，这是和其他语言的区别。GAMS 有很强的灵活性和通用性，通过以上几个算例也发现，GAMS 在运行效率方面也优先于其他软件，节省了开发者的时间，并且由算例（3）可知，GAMS 可对实际问题进行建模，并且能够很好的解决复杂的实际问题，做出合理的决策。GAMS 在编译方面也有优势，编译结束会生成详细的报告，适用范围较广，可以在各个行业发挥很大的作用。