系有绳索的水下浮体上浮性能仿真及实验研究∗
林舟曦 何世平
(1.海军工程大学动力工程学院 武汉 430033)(2.湖北工业大学机械工程学院 武汉 430068)
1 引言
关于浮体水中上浮的相关动力学模型国内外已经做了大量研究,也产生了很多设计应用,例如黄祥兵、黄兴玲、董云飞[1]对水下航行器集体逃生舱上浮过程进行了分析,建立逃生舱上浮模型并用数学方法和仿真软件验证了模型的可靠性。孙石、宋兆丽[2]分析了水球在水中的受力情况和能量变化,引入浮力势能概念,给出了水球上浮的理论模型。李志伟、崔维成[3]分析了深海载人潜水器的下潜上浮过程,推算出深海潜水器运动阻力估算公式。潘彬彬等[4]引入收缩率概念改进潜水器上浮与下潜的理论模型,并开发出了无动力潜浮过程的分析系统。徐萌萌[5]等对一种浮体自由上浮运动过程进行测量与研究,建立了浮体自由上浮的速度,位移与时间的理论模型与仿真结果并通过实验验证。Nur Afande AliHussain[6]等对水下航行器上浮下潜过程进行分析,建立了水下航行器平衡浮力数学模型。Michael Woolwright[7]设计了一种水下释放装置,用于救生筏的水下释放。Wainman[8]采用类似的滚筒、绳索以及浮体的机械结构,设计了一种应急浮标的水下释放装置等。
而对于携带绳子和滚筒的浮体上浮模型,在许多领域也可以见到。比如水雷的海底布置过程[9],水下航行器应急通信浮标释放,以及水下航行器上救生筏释放的上浮过程等物理过程。这些物理过程基本上在目前已经实现或是仍在研究中,但是适用于这些物理过程的理论模型以及相关的研究较少,虽然文献[5]对浮体上浮同样给出速度位移与时间的数学模型,但模型不考虑绳子和滚筒。因此,本文进行了进一步的研究,即对存在绳子和固定滚筒的浮体上浮过程进行研究,建立其理论模型,通过仿真,绘制出携带绳子和固定滚筒的浮体上浮过程速度,位移与时间的函数关系曲线图。最后根据实际救生筏水下释放实验,验证所建立的理论模型以及仿真结果具有一定的准确性,为这具有一定普遍性、多领域应用性的物理过程提供一个理论参考。
2 带绳子滚筒的浮体上浮过程动力学分析
因为实际实验的浮体近似球形,为了接近实验的实际情况,浮体简化为球体,建立模型后如图1所示。

图1 浮体、绳子、滚筒模型
对浮体模型作受力分析,如图2所示。
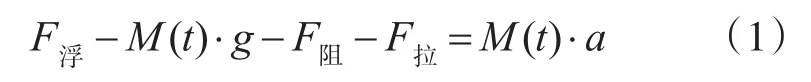
有些情况绳子的重量可以忽略不计,例如救生筏绳索系统,绳子轻。而有些情况绳子的重量不可忽略不计,例如水雷的水下释放,因为锚链的重量比较大,锚雷在上浮过程中,锚链的重量就不能忽略,但是这里本文统一考虑绳子重量,并用m(t)表示,读者可根据实际绳索情况确定绳子模型的线密度,从而确定绳子质量。

图2 受力分析
所以浮体上升的总质量为浮体质量与绳子质量之和:

环境是海水,因此浮体在海水中受到海水的流体阻力,因此:

而增加的质量与绳子的线密度以及从滚筒输送出来的长度有关,得:

式中:F浮为浮体受到的浮力,单位为N;M(t)为t时刻,浮体和绳子的总质量,单位为kg;M浮体为球形的浮体、救生筏以及相关设备的质量,单位为kg;F阻为海水阻力,单位为N;F拉为绳子拉力,单位为N;ps为海水密度,单位为kg/m3;pl为绳子线密度单位为kg/m;L(t)为t时刻绳子的长度,单位为m;c为水中阻力系数;A为垂直于来流方向的物体横截面积,单位为m2;vt为t时刻浮体上升的速度,单位为m/s。
对球形浮体上浮过程中的滚筒作受力分析,因为本次实验存在滚筒的制动装置,因此存在制动力矩,另外还需考虑滚筒中间的轴零件与其他零件相对运动产生的摩擦,因此还存在轴的摩擦力矩,但是制动装置制动也是采用摩擦力制动原理,并且两者都是常数,因此这里进行简化(制动装置忽略不画),统一用摩擦力矩表示,符号M摩,如图3所示。

图3 受力分析

因为绳子物理模型的拉伸量可忽略不计,所以浮体位移距离和滚筒外边缘释放的绳子长度,即滚筒外边缘的总线位移相同,即:

另外:

所以可得到:

式中:s总为浮体上浮位移,单位为m;α总为浮体上浮过程中,滚筒转过的总弧度,单位为rad;r为滚筒半径,单位为m;a为浮体上浮加速度,单位为m/s2;α为浮体上浮过程中,滚筒转动的角加速度,单位为rad/s2;M摩为滚筒滚动时受到的摩擦力矩,单位为N·m。J为转动惯量,单位为kg·m2。
联立式(1)~式(9),得到:

3 上浮过程仿真模拟及分析
3.1 仿真模拟图像
为了绘制浮体上浮的速度、加速度、位移以及绳子拉力和时间的关系曲线,使用实际测量的数据:M浮体=200kg,F浮=320N,g=9.8N/kg,J=0.6kg·m2,r=0.045m,ps=1025kg/m3,pl=0.1kg/m(钢丝绳),c=0.5,A=0.6,M摩=3N·m。并带入式(10),通过仿真计算,绘制曲线图如下。

图4 速度与时间的关系

图5 上升位移与时间的关系
3.2 仿真模拟结果分析
从位移图来看,浮体上浮过程总体比较接近直线,说明浮体上浮状态接近匀速运动。但从速度图像来看,速度先从零上升到最大速度,再渐渐下降,而文献[5]仿真的速度不会有明显下降,初步说明绳子的存在对浮体上浮有一定影响。
4 浮体上浮过程实验与分析
4.1 上浮实验数据采集
以救生筏水下释放为实验背景,气胀式救生筏一般用于水面船只上,并从水面释放,但是为了能够让其应用在水下航行器上,释放到水面后为遭遇事故后的水下航行器落水人员提供庇护所[10~12],本课题组制作出工程样机进行水下释放实验。本次实验中,救生筏安装在球形的浮体中,实验时,在滚筒上每250mm的钢丝绳处,绑上红色的防水胶,钢丝绳与浮体用尼龙绳绑定,白色尼龙绳上用蓝色油性笔每隔150mm做上记号。实验过程中用水下摄像机对准滚筒处进行录像(图6)。

图6 水下摄像机画面
本次总共进行了水下10m和水下25m的实验,释放实验结束后,对滚筒录像视频进行数据采集,计算出浮体上浮速度、位移与时间的关系,绘制曲线图(图7和图8)。实验时,浮体上浮到水面,因此,速度最终降至零点。

图7 速度与时间的关系

图8 位移与时间的关系
4.2 实验结果与理论的比较分析
将实验曲线与理论曲线进行比较(图9与图10)。

图9 速度比较

图10 位移比较
对比结果后总结如下:
采样的精度产生误差,本次实验中因为摄像机角度的原因,虽然同样是25m的长度,但是离摄像机越远,同样的长度在画面上所显现的距离就会越短,会给测量估计造成困难,因此在数据采样时会产生测量误差。
浮体离开释放装置后所达到的最大速度比较接近,都在2.5m/s~2.8m/s范围内。因此最大速度方面仿真模拟结果接近实际。
从速度趋势上来说,通过25m的实验曲线和仿真曲线的比较,可以发现,浮体的速度在到达最大速度后,都开始逐渐下降(文献5中实验结果速度没有明显下降)。说明浮体上浮过程中绳子的存在确实对浮体上浮产生了影响。因此速度趋势方面,所建立的模型与实际情况接近。
速度降低形式上,从25m释放的实验曲线结果可以看出,与文献[5]类似,速度产生了波动,可能原因是所建立的模型与本次实际实验有所差别。如图11和图12,在所建立的模型中,浮体从开始的释放到上浮整个过程中,绳子与球形浮体的连接点始终被认为处于浮体的正下方,然而实际在进行水下实验时,尼龙绳的一端是绑在浮体侧面上的,也就是说,实际实验时,浮体开始释放瞬间,会产生绕绳子与浮体连接点的翻转并很可能在之后的过程中形成周期性的摆动现象(图13),而且这种翻转或者摆动幅度现象可能在浮体上浮过程中,因为受到旋转周围的海水阻力而逐渐减小(类似机械阻尼结构的效果)。因此呈现出绳子与浮体的连接点产生速度起伏并且幅度降低的现象。此现象需要在今后试验中改进所建立的模型并继续研究。

图11 想象的安装情况

图12 实际安装情况

图13 浮体翻转
5 结语
1)实验结果浮体上浮过程所达到的最大速度与理论最大速度接近。
2)绳子的存在对浮体的上浮速度产生影响。
3)实验结果中,浮体上浮过程速度总体上逐渐降低的趋势特点与仿真结果相符合。
4)实验模型具有一定的准确性,但存在误差,并且所建立的模型需要改进。
5)仿真以及实验结果可以为本领域或是其他领域的同类物理过程的工程问题提供参考。

