弟6讲 “统计与概率”复习精讲
敖勇 程菊红
6.1 统计
考点、易混易错点解读
考点主要有总体与样本、“三数”(众数、中位数、平均数)的概念,平均数(或加权平均数)、极差、方差的计算,统计图(表)的分析.
样本容量指的是样本中个体数目,不要带上单位.
求中位数时应注意三点:(1)这组数据一定是按从小到大(或从大到小)排列好的数据.(2)搞清数据的个数.(3)弄清所解决问题中的数据是哪方面的数据.
高频考点例题点拨
一、抽样调查
例1 (2019.贺州)调查我市一批药品的质量是否符合国家标准,采用____(填“全面调查”或“抽样调查”)方式更合适.
解析;采用抽样调查方式更合适,
点拨:一般当调查个体数量不大时可用全面调查的方式,当数量较大且具有破坏性时用抽样调查的方式,
二、直方图、频率
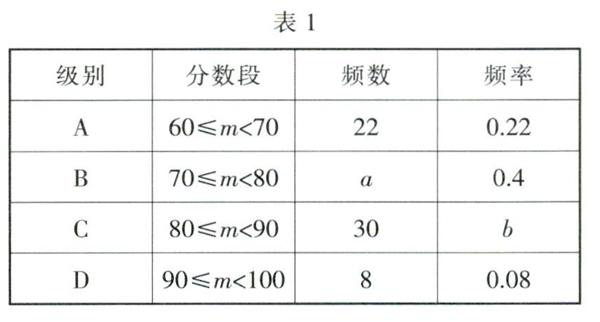
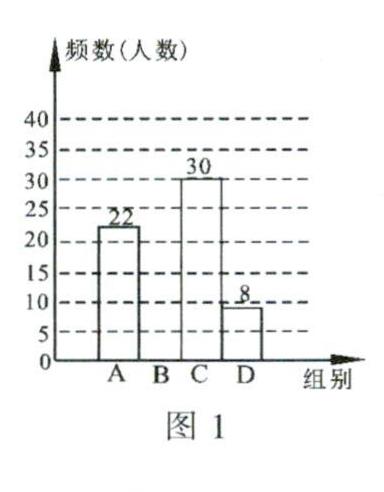
例2第十一届全国少数民族传统体育运动会于2019年9月在郑州市举行.全国各地少数民族运动员进行为期14天的民族式摔跤、少数民族武术、马术等17个项目的竞技和表演切磋.某校面向全体中学生举行了一次以“民族平等团结互助和谐”为主题的征文比赛(每位同学限1篇),每篇参赛作品成绩记为m(60≤m≤100)分,学校从中随机抽取了部分学生的参赛作品进行成绩统计,并将统计结果绘制成尚不完整的频数分布表和频数分布直方图(如表1、图1).
根据统计图表,解答下列问题.
(1)本次共抽取了
名学生的参赛作品进行成绩统计.
(2)频数分布表中a=____,b= ____.
(3)请补全频数分布直方图.
(4)若本校参赛选手共有1 200名,请估计其中成绩在80分以上(包含80分)的学生人数.
解析:(1)∵抽取的A组有22人,占抽取学生总数的22%,
∴本次共抽取22÷0.22=100(名)学生的参赛作品.
(2)a=0.4x100=40,b= 30 /100=0.3.
(3)补全频数分布直方图略.
(4)1 200x(0.3+0.08)=456(人),所以估计其中成绩在80分以上(包含80分)的学生人数为456.
点拨:由各组频率之和等于1,即可求出6的值.解答本题还要用到两个数量关系:数据总数×某组的频率=相应组的频数,各组数据之和等于抽样数据总数(样本容量).
三、扇形统计图、频率
例3 (2019.东营)为庆祝建国70周年,东营市某中学决定举办校园艺术节,学生从“书法”“绘画”“声乐”“器乐”“舞蹈”五个类别中选择一类报名参加,为了了解报名情况,组委会在全校随机抽取了若干名学生进行问卷调查,现将报名情况绘制成如图2所示的不完整的统计图.请你根据统计图中所提供的信息解答下列问题.
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求“声乐”类对应扇形圆心角的度数.
解析( 1)∵被抽到的学生中,报名“书法”类的人数是20,占被抽取学生总数的10%,
∴在这次调查中,一共抽取的学生人数为20÷10%=200.
(2)被抽到的学生中,报名“绘画”类的人数为200x17.5%=35,报名“舞蹈”类的人数为200x25%=50.
补全条形统计图略.
(3)被抽到的学生中,报名“声乐”类的人数为70.
∴扇形统计图中,“声乐”类对应扇形圆心角的度数为70/200×360°=126°.
点拨:解答本题用到的数量关系为:各组数据之和等于抽样数据总数(样本容量);在扇形统计图中各部分百分比之和等于1,某组所在扇形圆心角的度数=该组所占百分比x360°.
中考命题预测
1.下列说法中正确的是( ).
A.“打开电视,正在播放《新闻联播》”是必然事件
B.“x2<0(X是实数)”是随机事件
C.掷一枚质地均匀的硬币10次,可能有5次正面向上
D.为了了解夏季冷饮市场上冰淇淋的质量情况,宜采用普查方式调查
2.如表2记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( ).
A.甲
B.乙
C.丙
D.丁
3.某校为了解本校学生对2019年国庆活动的了解情况(分为“十分了解”“基本了解”“了解较少”“不了解”四种情况),随机抽取了九年级部分学生进行调查,绘制成如图3、图4所示的不完整的统计图,请根据图中信息,回答下列问题.
(1)本次接受调查的学生有____名,图3中的a=__b=____.
(2)“了解较少”对应的圆心角的度数为
(3)请补全条形统计图.
(4)若该校九年级共有1500名学生,请估计对2019年国庆活动“基本了解”的学生有多少名.
4.为响应传统文化进校园的号召,某校七年级、八年级举行了“诵读经典”读书比赛活动,現从该校七、八年级中各随机抽取15名学生的比赛成绩(百分制)进行整理、描述和分析,x(单位:分)表示成绩得分,共分成四组:A. 80≤x<85,B.85≤x<90,C.90≤x<95.D.95 ≤x≤ 100.下面给出了部分信息.
七年级15名学生的诵读经典的成绩如表3.
八年级15名学生的竞赛成绩在C组中的数据是:92,91,94,90,94.八年级抽取的学生竞赛成绩的统计图如图5.
七、八年级抽取的学生诵读经典的成绩统计结果如表4.
根据以上信息,解答下列问题:
(1)直接写出上述表中a=____,b=____________________.
(2)该校七、八年级各1 000人参加了诵读经典的读书活动,参加此次竞赛活动成绩在94分以上的(含94分)为优秀,成绩优秀的学生都会获得一本经典名著的獎励,那么七、八年级共约有多少人会获得该奖品?
6.2 概率
考点、易混易错点解读主要考点有不可能事件、必然事件与随机事件的判断、概率的计算(列表法、画树状图法).常见的问题背景有“摸球”“抽卡片”“转转盘”.概率与统计的综合问题是近几年中考的考查重点.
当一次试验涉及三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用画树状图法求概率.
易混易错点是:涉及两步试验的概率问题中有“放回”与“不放回”两种情形,容易混淆,应注意区分.
高频考点例题点拨
一、用列表或画树状图法求概率
例1在一个不透明的袋子中装有3个除了颜色其他完全相同的小球,其中有1个白球、1个黄球、1个红球,摸出一个球记下颜色后放回,再摸出一个球,请用列表法或画树状图法求两次都摸到红球的概率,
解析:画树状图如图1.共有9种可能情况,两次都摸到红球的有1种可能情况,故概率为1/9.
点拨:解答此题需要注意“放回”两个字,“放回”和“不放回”的情形结果不一样.
例2(2019.河南)现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除了颜色其他完全相同.从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是.
解析:一个袋子中的两个红球记为红1、红2,另一个袋子中的两个红球记为红3、红4列表如表1.
由表知,共有9种可能结果,其中摸出的两个球颜色相同的有4种结果,所以摸出的两个球颜色相同的概率为4/9.
点拨:当一次试验涉及两个因素且出现的结果数目较多时,为了不重不漏地列出所有可能的结果,通常采用列表法,易错点是不能正确判断试验涉及几个因素或者几步随机事件.
二。统计与概率的综合问题
例3(2019.包头)某校为了解九年级学生的体育达标情况,随机抽取50名九年级学生进行体育达标项目测试,测试成绩如表2,请根据表中的信息,解答下列问题.
(1)该校九年级有450名学生,请估计体育测试成绩为25分的学生人数.
(2)该校体育老师要对本次抽测成绩为23分的甲、乙、丙、丁4名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.
解析:(1)∵样本中成绩为25分的学生人数所占比例为18/50×100%=36%,
∴估计总体中成绩为25分的学生人数所占比例也为36%.
∴450名学生中,成绩为25分的学生估计有450x36%=162(人).
(2)列表如表3.
共有12种可能的结果,其中甲、乙恰好分在同一组的结果有(甲,乙)、(乙,甲)、(丙,丁)和(丁,丙)四种结果.
∴P(甲、乙恰好分在同一组)=4/12=1/3,
点拨:本题综合考查统计与概率的知识,根据概率的求法,关键要找准两点:①全部情况的总数,②符合条件的情况数目.易错点是不能不重不漏地列出所有可能的情况,
中考命题预测
1.一个不透明的袋中共有4个球,它们除了颜色不同,其余均相同,其中有1个白球、2个黄球、1个绿球.随机摸出一个小球后放回,再随机摸出一个小球,则两次摸出的小球是一个白球、一个黄球的概率为( ).
A.2/3.
B.1/3
C.1/4
D 1/2
2.小强同学从-1,0,1,2.3,4这六个数中任选一个数,满足不等式x+1<2的概率是( ).
A.1/5 B.2/4 C.1/3 D.1/2
3.有一枚质地均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6.若任意抛掷一次骰子,朝上的面的点数记为x,计算x-5,则其结果为非负数的概率是( ).
A.1/6 B.1/4 C.1/3 D.1/2
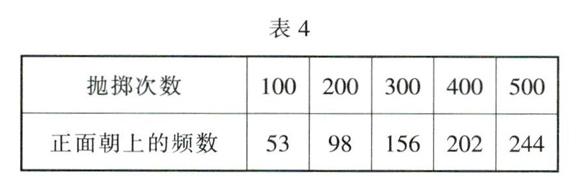
4.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表4.
若抛掷硬币的次数为1 000.则“正面朝上”的频数最接近( ).
A.20 B.300 C.500 D.800
5.在一个不透明的盒子里,装有三个分别标有数字1,2,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y
(1)写出(x,y)的所有可能出现的结果.
(2)小明、小华各取一次,由取出小球所确定的数字作为点的坐标,这样的点(x,y)中落在反比例函数y=4/x的图象上的点的概率是多少?
作者简介
敖勇,河南省学术技术带头人,河南省级骨干教师,河南省教师培训师.在《中学数学教学参考》《中学生数理化》等刊物上发表论文30多篇,《中考专家》《试题研究》等图书的编委和作者之一,《中学数学教学参考》特约编辑。
———《扇形的认识》教学廖
- 中学生数理化·中考版的其它文章
- 第4讲 “图形的性质”复习精讲
- 第5讲 “图形的变化”复习精讲
- “中考命题预测”参考答案

