尾矿连续沉积过程中超孔隙水压力演化的温度-渗流-力学-化学耦合模型*

李西龙 张发源 丁培培 张 露 周家文 鲁功达

(①四川大学水力学与山区河流开发保护国家重点实验室，成都 610065，中国)(②四川大学水利水电学院，成都 610065，中国)

0 引 言

地下采矿是为社会经济发展提供物质资源的必要途径，但在其实施过程中不可避免地产生了大量的尾矿废弃物和地下采空区，严重威胁着矿山安全生产和自然生态环境(徐文彬等，2015；吴爱祥等，2016；林海等，2019)。尾矿的常规地表处置方法具有尾矿坝溃决和酸性废水排放导致水源污染等风险，而地下采空区的存在则可能造成井下岩石冒落以及地表塌陷等一系列的工程和环境问题。尾矿胶结充填技术通过将水、胶结剂(如水泥等)和尾矿形成的混合物回填至矿柱开采后残留的采空区，不仅能够避免尾矿等固体废弃物在地表的曝露堆积，还能改善井下采场围岩稳定性并提高矿石回采率。该尾矿-采空区协同处置技术已成为突破现有资源、能源、环境制约瓶颈的重要技术途径之一(马凤山等，2015，2018；Witteman et al.，2017；刘锋等，2018；吴爱祥等，2018)。

回填至地下采空区后，尾矿充填体的力学特性将在温度-渗流-力学-化学场的耦合作用下产生复杂的时空演化(Ghirian et al.，2013，2014)。充填系统的稳定性取决于充填体作用在挡墙上的压力。一般地，沉积速率越慢，尾矿中的孔隙水压力越低，有效应力越高，作用在挡墙上的压力越小，充填体稳定性越好，但充填作业效率较低。因此，揭示尾矿连续充填过程中的多场耦合作用对孔隙水压的影响机理，对优化不同开采环境条件下的充填技术、进而实现矿山安全高效开采具有重要意义。

前人针对多场耦合作用下的充填体行为特性开展了大量的试验工作(Klein et al.，2006；Fall et al.，2010；Ghirian et al.，2013，2014)，但这些研究均以充填完成后的尾矿为研究对象，因此无法揭示连续沉积过程中充填体孔隙水压的演化规律。Helinski et al.(2011)、Doherty(2015)、Muir Wood et al.(2016)、以及Lu(2017); Lu et al.(2020)开发了尾矿充填体的化学固结模型，但上述研究均未考虑温度对充填体行为特性的影响。Cui et al.(2018)建立了尾矿充填体的温度-渗流-力学-化学耦合模型，但忽略了固体颗粒和孔隙流体的可压缩性以及水的热膨胀效应，因此难以准确描述复杂赋存环境中充填体的孔隙水压力。

本研究基于经典Biot孔隙弹性理论建立尾矿的温度-渗流-力学-化学(THMC)耦合模型框架，进而推导连续沉积过程中尾矿热-化学固结的一维超孔隙水压力模型，通过分析不同沉积速率、不同初始和边界温度条件下的充填过程，揭示多场耦合作用对尾矿超孔隙水压力的影响机理。

1 饱和尾矿充填体的温度-渗流-力学-化学耦合模型框架

1.1 建模方法

本研究利用质量、动量和能量守恒定律建立温度-渗流-力学-化学耦合条件下饱和尾矿充填体的理论模型框架。模型中不考虑机械能和热能的相互转换，假设固液两相满足局部热平衡条件且两者均具有可压缩性，模型中的化学反应速率、水的动力黏度以及热膨胀系数与温度直接相关。根据连续介质力学惯例，固相压为负，液相压为正。模型中所考虑的化学-物理过程如图1所示。在水泥水化反应造成水的相变过程中，孔隙水体积减小而固体颗粒体积增加，尾矿孔隙度减小。

图1 模型中考虑的化学-物理过程

1.2 化学反应

随着水泥水化放热反应的进行，尾矿中的孔隙流体逐渐被消耗。同时，水泥的化学反应还将造成尾矿孔隙度、刚度和渗透性的变化。为考虑化学反应速率的温度敏感性，本研究采用Arrhenius定律将绝对温度T下的化学反应时间t转换为参考温度Tr下的等效化学反应时间te(Schindler，2004)：

(1)

式中：Ea为化学反应需要的活化能；Ra为通用气体常数(8.314iJ·mol-1·K-1)。

1.3 能量守恒

同时考虑化学反应放热以及热传导和热对流的尾矿能量守恒方程可以表示为：

(2)

1.4 质量守恒

饱和尾矿中固体和液体的质量守恒方程可以表示为：

(3)

(4)

(5)

式中：α=1-[Kd(te)/Ks]为Biot系数；Kd(te)、Ks和Kw分别为尾矿固体骨架、固体颗粒和液态水的体积模量；βs和βw为固体和流体组分的热膨胀系数；εv为体积应变。

1.5 动量守恒

饱和条件下尾矿的力学平衡方程可表达为：

·σ+[(1-n)ρs+nρw]g=0

(6)

式中：总应力张量σ与有效应力张量σ′和孔隙水压力的关系为：

σ=σ′-αpwδij

(7)

非等温条件下尾矿的增量型应力-应变关系可表达为：

dσ′=Ddε-Kd(te)βsdTδi

(8)

式中：D为弹性张量；ε为应变张量。

1.6 孔隙度演化

联立式(3)和固相的状态方程可得到仅由温度-渗流-力学耦合作用引起的孔隙度变化速率：

(9)

在水泥水化过程中液态水转变为固态水，则化学反应造成单位体积尾矿的孔隙度变化可以表达为n=n′+εd(te)，其中相变产生的固态水体积εd(te)=4.26εsh(te)(Lu，2017)。因此，尾矿的孔隙度变化速率可由下式描述：

(10)

2 连续沉积过程中尾矿热-化学固结的一维超压模型

为厘清尾矿在多物理场耦合作用下的行为特性演化规律，本研究将基于前文建立的THMC耦合模型推导尾矿连续沉积过程的一维热-化学固结模型。对于基底以上高度为z的单元，其化学反应将在该点被上覆尾矿掩埋后开始(即t≥z/m，其中，m为沉积速率)。

一维条件下的能量守恒方程(式(2))可改写为：

(11)

类似地，质量守恒方程(式(5))的一维形式可表达为：

(12)

式中：K(te)为尾矿的导水系数。

由于一维条件下总应力的变化仅由新沉积尾矿的自重引起，则有效应力方程(式(7))可改写为：

-γ(mt-z)=σ′-αpw

(13)

由式(6)可得γ=[(1-n)ρs+nρw]g=(1-n)γs+nγw。

同时，孔隙水压力可以分解为超孔隙水压力(u)和静水压力两个部分：

pw=u+γw(mt-z)

(14)

将式(14)代入式(13)可得：

σ′=αu+(α-1)γw(mt-z)-γ′(mt-z)

(15)

式中：γ′=γ-γw。

一维条件下的骨架本构关系(式(8))可表达为：

(16)

式中：E0(te)为约束模量；v为泊松比。

将式(15)代入式(16)可得到沉积过程中的尾矿沉降速率：

(17)

再将式(14)和式(17)代入式(12)，最终得到沉积过程中的超压控制方程为：

(18)

式中：沉积速率、热膨胀、渗流(排水)以及水化耗水作用对尾矿超压的影响不言自明。

类似地，由式(10)可得到一维条件下的孔隙度变化率为：

(19)

将式(14)和式(17)代入式(19)可得：

(20)

以上非线性偏微分方程组(式(1)、式(11)、式(18)和式(20))构成了连续沉积过程中尾矿热-化学固结作用的动边界问题。本研究利用COMSOL Multiphysics软件对该控制方程组进行数值求解。

3 模型验证

本研究利用Helinski et al.(2011)开展的尾矿现场充填试验验证所建立的尾矿连续沉积过程的一维热-化学固结模型。计算中使用的尾矿物理-化学参数如表1所示，沉积过程中尾矿充填体的深度变化如图2所示。

表1 尾矿的物理-化学性质

图2 模拟计算与现场监测的孔隙水压力对比

尾矿的导水系数可表达为K(te)=k(te)γw/μw，其中，k(te)是固体骨架的固有渗透系数，而由于水的动力黏度μw是温度的函数(表1)，因此尾矿的渗透性将随温度的变化而变化。假设尾矿的初始温度(T0)与围岩边界温度(Tb)相同，本研究在该矿区(澳大利亚，Kalgoorlie)5～35i℃年温变化范围内求解完整的控制方程组。计算所得采空区底部的孔隙水压力与现场测量结果的对比如图2所示。结果表明，在所考虑的区域温度范围内，模型计算结果与实验数据吻合较好。

4 温度-渗流-力学-化学耦合作用对尾矿超压的影响机理

为揭示温度-渗流-力学-化学耦合作用对尾矿超孔隙水压力的影响机理，本研究利用尾矿连续沉积过程的一维热-化学固结模型分析不同沉积速率、不同初始和边界温度条件下的充填过程，计算中使用的尾矿物理-化学参数如表1所示。

4.1 温度-渗流-力学耦合作用对尾矿超压的影响机理

假设未经水泥处理(te=0)的尾矿以不同的初始温度沉积到温度为50i℃的不透水边界上，尾矿的沉积速率m=0.1im·h-1，采空区的高度为10im。尾矿的初始温度T0为10～50i℃。沉积结束时尾矿中的超孔隙水压力分布计算结果如图3所示。

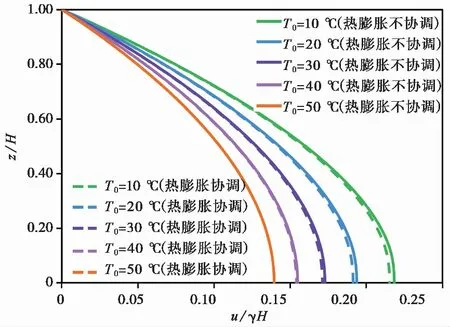
图3 初始温度对尾矿超压的影响

从图3可知，尾矿的初始温度越高，水的动力黏度越小，尾矿的导水系数越大，排水越快，因此相同深度处的超孔隙水压力越小。由图中还可看出，尾矿的初始温度和边界温度差异越大，沉积边界处尾矿的热膨胀变形也越大，因此固液两相热膨胀不协调时的超压与两者热膨胀协调时的差异也越大。

4.2 温度-渗流-力学耦合作用对水化升压的影响机理

假设长为0.1im的反压饱和尾矿试样(m=0)被置于不排水的绝热环境中。该试样在不同初始温度条件下的孔压和温度演化计算结果如图4和图5所示。

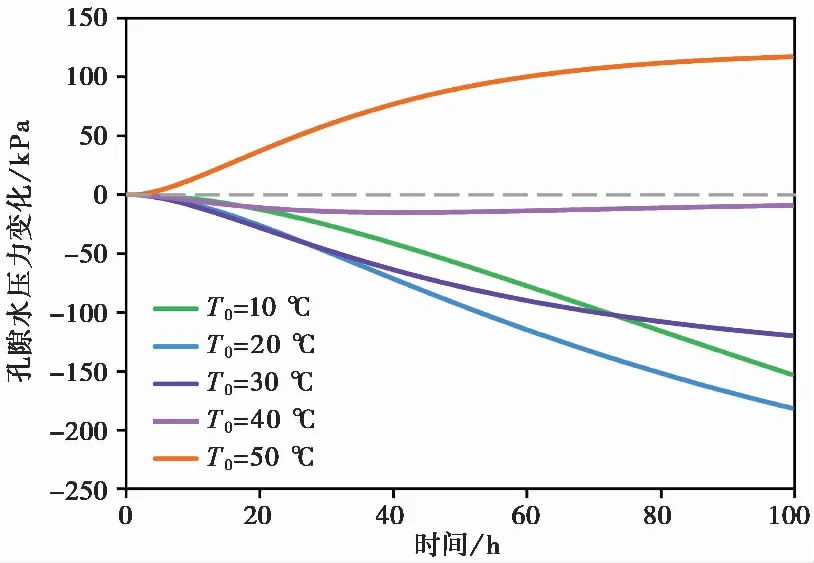
图4 不同初始温度下水化反应造成的孔压变化

图5 不同初始温度下水化反应造成的温度变化

由图4和图5可见，虽然水泥水化过程消耗孔隙水进而降低了孔压，但水化放热反应造成的温升同样可通过流固两相不协调的热膨胀造成孔压上升。从图4中还可以看出，这两种竞争机制在不同温度区间对孔压的影响程度具有显著差异。

初始温度在10～20i℃时的化学反应较慢，水化放热引起的温升小，因此水化耗水对孔压的降低作用占主导地位；随着温度升高，水化反应耗水加快，因此20i℃比i10℃时的孔压更低。当初始温度超过20i℃时，随着初始温度升高，水化放热造成的温升增加(图5)，进而使得流固不协调热膨胀造成的孔压上升增大、并在一定程度上抵消了水化耗水对孔压的降低作用。因此，在40i℃时，化学反应初期的水化耗水起控制作用，此时孔压小幅下降；随着化学反应进行，试样温度上升至临界温度，此时水化放热造成的热膨胀起控制作用，孔压随着化学反应的进行而增加。而当初始温度为50i℃时，水化放热造成的热膨胀完全抵消了水化耗水对孔压的降低作用，此时孔压随着化学反应的进行单调上升。

为推导化学反应造成水压升降的临界温度，现忽略尾矿试样(m=0)中的水力梯度(无渗流作用)，则超压的控制方程式(18)可简化为：

(21)

若不考虑试样中的热传导和热对流，则能量守恒方程式(11)可简化为：

(22)

将式(22)带入式(21)，同时考虑水化耗水与放热的同步性，可得到：

(23)

由于式(23)中的第1和第3项恒为正，因此化学反应造成水压上升或下降仅取决于其第2项：

(24)

式(24)中除水的热膨胀系数βw以外的参数均为常数或变化较小，因此可利用尾矿的初始参数获得如图6所示的f(T)随温度的变化规律。图6表明，当尾矿温度在45i℃以下时，水化耗水起控制作用，化学反应将造成水压降低；而当尾矿温度超过45i℃时，水化放热造成的热膨胀起控制作用，化学反应将造成水压上升。因此，化学反应造成该尾矿水压升降的临界温度为45i℃。该结论与图4所示的水压变化规律一致，且与Thompson et al.(2012)在现场监测中发现的尾矿水压异常上升时的温度较为吻合。

图6 f(T)随温度的变化规律

4.3 温度-渗流-力学-化学耦合作用对尾矿超压的影响机理

假设初始和边界温度为10i℃或50i℃的尾矿以不同的沉积速率填充至高度为10im的采空区中，充填结束时尾矿中的温度与超压分布计算结果如图7所示。

图7 充填结束时尾矿中的温度与超压分布

当沉积速率为m=0.75im·h-1时，由图7a1中较小的温度分布范围可知，此时充填体的化学反应尚不充分。根据4.1节的结论，沉积速率较快时尾矿中的超压将由初始温度对导水系数的影响控制、并同时受热膨胀作用的影响。因此，初始温度更高的充填体超压更低；此外，当低温充填体沉积到高温采空区时(T0=10i℃，Tb=50i℃)，边界处的热膨胀作用将造成超压的显著上升，而当高温充填体沉积到低温采空区时(T0=50i℃，Tb=10i℃)，边界处的充填体受冷收缩，进而造成了超压降低(图7b1)。

当沉积速率降低至m=0.05im·h-1时，图7a2表明此时化学反应造成的充填体温度上升明显，水化反应对超压的影响增大。当初始温度与边界温度相同时(T0=Tb)，高温(50i℃)充填体在高于临界温度(45i℃)的条件下水化，而低温(10i℃)充填体在低于临界温度的条件下水化，因此前者超压更大。同时由于沉积速率较慢，充填体与边界围岩将产生更充分的热交换。当高温充填体沉积到低温采空区时，虽然上部充填体在高于临界温度的条件下水化，但其下部在低温边界作用下将产生冷却收缩并发生低于临界温度的水化反应，因此超压随深度的增加而降低；相反地，当低温充填体沉积到高温采空区时，其上部发生低于临界温度的水化反应，而充填体下部在高温边界作用下产生热膨胀并产生高于临界温度的水化反应，因此超压随深度的增加先减小后增大(图7b2)。

5 结 论

本研究提出了连续沉积过程中尾矿热-化学固结的一维超压模型，分析了初始温度、边界温度、填充速率等因素对尾矿超孔隙水压力的影响机理，获得的主要结论如下：

(1)当沉积速率较快或化学反应不充分时，充填体的初始温度越高，水的动力黏度越小，充填体导水系数越大，排水越快，因此超孔隙水压力越小。当沉积速率降低时，水化反应对充填体超压的影响增大。

(2)虽然水泥水化过程消耗孔隙水进而降低了超压，但水化放热反应造成的温升同样可通过热膨胀造成水压上升。在不排水的绝热环境中，这两种竞争机制在不同温度区间的不同贡献共同决定了尾矿超压的变化规律。当尾矿温度在45i℃以下时，水化耗水起控制作用，化学反应造成水压降低；而当尾矿温度超过45i℃时，水化放热导致的热膨胀起控制作用，化学反应造成水压上升。

(3)低温边界可导致充填体受冷收缩并降低水化反应温度，进而造成水压降低；而高温边界可导致充填体受热膨胀并提高水化反应温度，最终造成水压上升。