水平岩土层实体拦砂坝基底水压力研究*

刘 茂 袁 磊 张 鹏

(四川省地质工程勘察院集团有限公司，成都 610072，中国)

0 引 言

泥石流是地质灾害中危害较大的一种自然灾害类型，地震过后，泥石流灾害将成为震后的主要地质灾害，且震后效应将持续较长一段时间(何朝阳等，2018)。目前，由于其结构简单、经济、施工方便和耐久性等特点，拦砂坝在泥石流灾害治理中得到了极其广泛的应用，文家沟、兴坪沟等泥石流沟都采用了实体拦砂坝或者将其作为治理措施的一个重要部分(冯文凯，2017；许强，2017)。然而其稳定性和坝基渗透变形成为了该类坝体设计的关键，且影响坝基稳定性的扬压力和坝基渗透破坏的研究是一个棘手的问题，这些都与实体拦砂坝和坝基岩土体组成的渗流系统有关；渗流引起的渗透破坏是造成堤防、基坑和地下工程破坏的主要原因，因此，开展土的渗透稳定性研究非常重要(齐俊修等，2017)。

影响拦砂坝坝基扬压力和地基土的水力条件的因素很多，诸多学者采用室内试验的方式对拦砂坝的基底扬压力进行了研究。研究表明，坝前堆积物的渗透性对坝底扬压力影响显著，渗透性越好，作用于坝底的扬压力越大，反之则越小，当坝底为均质土时，自坝踵至坝趾沿程的水头不断降低，扬压力也呈线性降低；沟床坡度对坝底扬压力的影响显著，沟床坡度越大，作用于坝底扬压力越小，当坝前有堆积物时，以上两种影响扬压力的变化规律更加明显(关辉等，2017；陈兴长等，2018)；通过研究实体坝坝基土颗粒级配和泥石流坝前沉积特征对坝基扬压力的影响和变化规律，得到了坝基扬压力折减系数与坝基土渗透系数、颗粒级配有很大关系(张莉等，2018a，2018b)。还有学者借鉴水工坝坝底扬压力的计算方法，根据扬压力沿坝基轴线呈线性分布的特点，考虑基于坝前泥石流浆体细颗粒浓度，研究了一种计算拦砂坝坝基扬压力折减系数的方法(游勇等，2018)。

现阶段，关于实体拦砂坝的稳定性和坝基渗透变形主要还是采用水工方面的计算公式进行设计验算，在很大程度上还是依靠经验来估算重力实体坝的一些参数，很多还是基于室内试验或者野外实验得到的基本规律和特定条件下的研究结论。本文借助Ridder(1994)针对河流渗入半封闭含水层模型的计算思想，试图尝试采用流体连续性原理、达西定律和伯努利表达式，在合理的假设条件下，结合实体拦砂坝的基本特点，推导了关于实体拦砂坝基底关键部位的测管水头解析表达式，利用该解析表达式可以方便地确定实体拦砂坝坝基下的水压力，也可以方便地确定建构筑物(实体坝坝体(包括护坦))下游x处的水力梯度(水力坡降)，进而结合土体类型划分可能发生渗透变形的范围，间接地为护坦设计提供依据，也可以评估已有实体拦砂坝的渗透稳定性，以及需要处理的范围和处理的方案设计。

1 模型及公式推导

1.1 模 型

假设条件：

(1)各含水层均质、各向同性；

(2)渗流为二维流且服从达西定律；

(3)含水层为水平渗流，半渗透性层为竖直渗流；

(4)水为不可压缩流体；

(5)水位上升为瞬时上升。

依据以上假设条件，具体模型见图1。

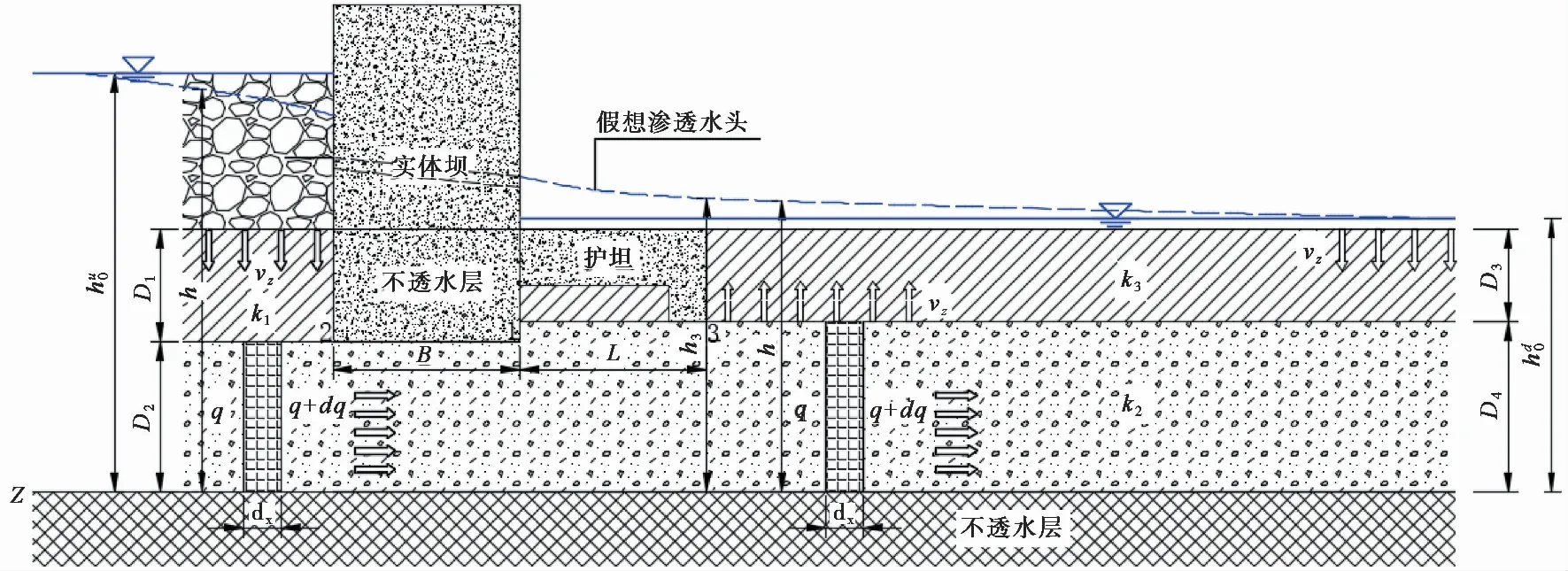
图1 水平岩土层实体拦砂坝稳定渗流模型

(1)

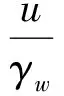
由于土体中渗流阻力大，渗流流速v一般很小，流速水头可忽略不计，因此，总水头可用测管水头(位置水头+压力水头)来代替(莫乃榕，2002；倬云芳，2003；Brutsaert，2005；王晓东，2006)。

(2)

依据达西定律(Darcy，1856；Hubbert，1956；Brutsaert，2005)：

(3)

(4)

式中：q为单位面积单位时间水通过的体积(m3)；Q为单位时间通过系统的水量(m3·s-1)；A为水流通过的横截面面积(m2)；v为通过土体横截面的平均名义流速(m·s-1)；k为关于渗透性的相关系数(m·s-1)；h1，h2为两端的测压管水头(m)(注意区别于压力水头)；L为渗流路径长度(m)。

1.2 公式推导

把渗流模型分为3部分，构筑物上游为第1部分，建构筑物(实体坝及下游护坦)为第2部分，构筑物下游为第3部分，分别单独进行渗流验算。

第1部分：实体坝及附属构筑物以上区域。

设实体坝的坝踵为坐标零点，水平轴为x轴，且向上游为正，竖直轴为y轴，且向上为正。

(5)

(6)

(7)

(8)

(9)

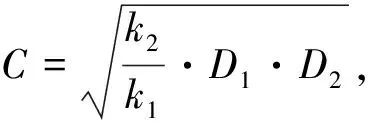
(10)

(11)

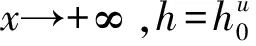
x=0，h=h2(未知)

因此，

(12)

实体坝坝踵处的含水层通过的流量：

(13)

当x=0时，

(14)

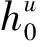
第2部分：实体坝及附属构筑物范围区域。

建构筑物(实体坝)基础下含水层横截面的流量：

(15)

建构筑物(下游护坦)基础下含水层横截面的流量：

(16)

式中：Qx，12为实体坝基础下地基的单宽流量(m3·m-1)；Qx，23为护坦下地基的单宽流量(m3·m-1)；D4为护坦下土体的厚度(m)；h1为实体坝坝趾处的测管水头(m)；h3为护坦尾部处的测管水头(m)；其余同上。

第3部分：实体坝及附属构筑物以下区域。

设护坦尾为坐标零点，水平轴为x轴，且向下游为正，竖直轴为y轴，且向上为正。

(17)

(18)

(19)

(20)

(21)

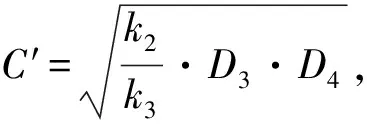
(22)

(23)

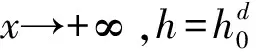
x=0，h=h3(未知)

因此，

(24)

构筑物(护坦)下游处的含水层通过的流量：

(25)

当x=0时，

(26)

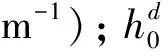
依据连续性原则，在构筑物下方通过的流量相等，可得：

(27)

(28)

(29)

(30)

(31)

(32)

2 解析解与数值模拟对比

假设实体拦砂坝基础底宽10im，护坦长15im，实体拦砂坝上游上层土体厚度(D1)为3im，渗透系数为k1，下层土体厚度(D2)为5im，渗透系数为k2，实体坝下游上层土体厚度(D3)为2im，渗透系数为k3，下层土体厚度(D4)为6im，渗透系数为k2，上游测压管水头为13im，下游测压管水头为9im。有限元模型见图2，有限元模型尺寸长120im，网格采用四边形网格，网格单元尺寸为0.5im，实体拦砂坝迎水面采用固定水位边界，水位为13.0im，背水面也采用固定水位边界，水位为9.0im，采用此模型的解析解与有限元数值模拟(Autobank有限元程序)的结果进行比较，验证其可靠性和稳定性。

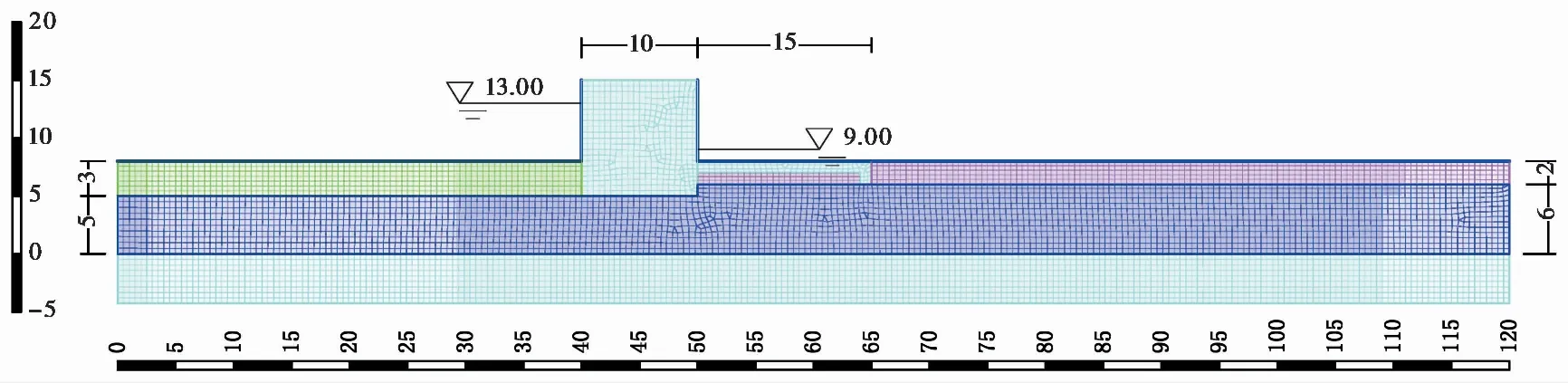
图2 水平岩土层实体拦砂坝稳定渗流有限元模型(单位：m)

由表1 和表2 计算结果可知：本文的解析式计算结果与数值分析结果误差非常小，基本上都小于1%，上游上层渗透系数较小时，h2的解析解大于数值解，误差基本上小于0.1%，上游上层渗透系数较大时，h2的解析解小于数值解，误差随着上游上层渗透系数增大，误差变大；h1和h3的解析解较数值解大，且h1比h3的误差大，h2介于h1和h3之间。利用该解析方法得到的测管水头与数值解基本一致。

表1 解析解和数值分析计算成果差异(k1≠k3)

表2 解析解和数值分析计算成果差异(k1=k3)

3 应用与讨论

3.1 应 用

依据上述计算公式得到关键点处的位置水头，可得到如下几点应用：

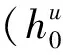
(2)为实体坝稳定性评价中涉及的坝基底部扬压力提供基本理论依据。

(3)依据坝基土体结构，确定护坦的合理设计长度和细部结构尺寸。

3.2 讨 论

在透水地基上的堤坝浸润线位置问题上，存在一个“地基的有效深度”概念，《渗流计算分析与控制》一文中描述：“当地基深度加大时，地基深度变化引起浸润线位置的变化，仅在一定深度范围内显著，当地基更深时，浸润线位置实际上已不再改变，地基的有效深度可取为he=0.5～1.0(L+m1H1)。”(毛昶熙，2003)。

依据以上经验，当实体坝坝基底部土体厚度大于“地基有效厚度”时，实体坝底部水压力解析式是否也可考虑“地基的有效深度”的影响，有待进一步的研究验证。

实际上，大部分拦砂坝是修建于具有一定坡度的沟道内，且坝体下游附属构筑物也具有一定的坡度，还有岩土层也并非水平分布，本文是针对水平分布岩土层的实体坝坝基底部关键点的位置水头解析式进行研究，很多学者已有研究证明沟床坡度对坝基底部水头具有一定的影响，这种修建于具有一定坡度的沟床上的实体坝坝基水压力解析式有待进一步分析研究。

4 结 论

(1)依据连续性方程和达西定律以及伯努利表达式，基于一定的假设条件下，推导了修建于水平岩土层的实体拦砂坝基底处关键点的水压力解析式。通过与数值模拟结果比较可知，本文的解析式计算结果与数值分析结果误差非常小，基本上都小于1%，上游上层渗透系数较小时，h2的解析解大于数值解，误差基本上小于0.1%，上游上层渗透系数较大时，h2的解析解小于数值解，误差随着上游上层渗透系数增大，误差变大；h1和h3的解析结果较数值解大，且h1比h3的误差大，h2介于h1和h3之间，利用该解析方法得到的测管水头与数值解基本一致，该解析方法是可靠稳定的。

(2)进一步讨论了该方法的应用价值，依据计算得出的h3后，可依据第3部分水头方程计算构筑物下游x处的水力坡降，判断护坦下游土体的渗透变形类型，也可估算需要处理的范围；另一方面可以对护坦的长度进行设计。

(3)当实体坝坝基底部土体厚度大于“地基有效厚度”时，实体坝底部水压力解析式是否也可考虑“地基的有效深度”的影响，有待进一步的研究验证。本文在水平分布的岩土层的基础上进行研究，但修建于具有一定坡度的沟床上的实体坝坝基水压力解析式有待进一步分析研究。依据相关文献，构筑物基底处的扬压力随着沟床坡度增大，扬压力有整体减小的趋势，运用该解析式对修建于有坡度的沟床的拦砂坝基底扬压力偏于安全。