数学问题解答
2020年8月号问题解答
(解答由问题提供人给出)

图1
2556如图1,已知Rt△MNT,∠MTN=90°,点O是MN中点,点I、J是TM、TN上的点,满足OI⊥IJ,点X是IJ中点,点Y是MN上的点,满足∠NIY=∠TMN,证明:XY⊥MN.
(安徽省滁州中学 李伟健 239000)

图2
证明如图2,延长IO至点Q,使得OQ=IO,
连接QM、QN、QJ,
则四边形IMQN是平行四边形,
则∠TNQ=90°,
所以点I、J、N、Q共圆,
得∠IQJ=∠INJ.
连接OX,那么OX∥QJ,
所以∠IOX=∠IQJ,
得∠IOX=∠INJ,则∠IXO=∠TIN,
又∠NIY=∠TMN,
所以∠IYM=∠TIN,则∠IXO=∠IYM,
得点I、Y、O、X共圆,
所以∠XYO=90°,即XY⊥MN.
2557已知正数a,b,c满足a+b+c=3,求证:
(河南省南阳师范学院软件学院2017级9班 李居之 孙文雪 473061)
证明不妨令x=ab+bc+ca,

由舒尔不等式及其变形得
(a+b+c)3-4(a+b+c)(ab+bc+ca)+9abc≥0,
所以3abc≥4x-9,
则所证不等式等价于
abc(x+3)+48≥9(x+3),
所以只需证明
(x+3)(4x-9)+144≥27(x+3)
⟺4x2-24x+36≥0
⟺(x-3)2≥0显然成立,
从而原不等式成立,
当且仅当a=b=c=1时等号成立.
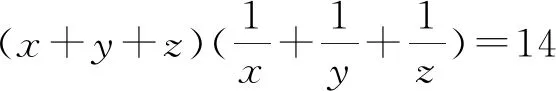
(浙江省慈溪市慈溪实验中学 华漫天 315300)
解不妨令m=x+y+z,
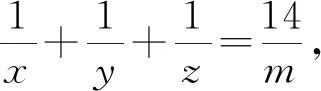
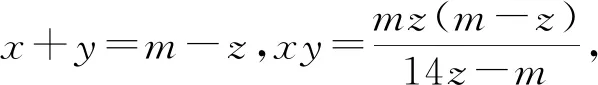
所以x、y是方程
的两根

显然m-z>0,

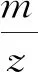
则m2-11zm+14z2≤0,


yzm+zxm+xym=14xyz,
而(x,z)=1,(y,z)=1,所以z|m;

代入原方程逐一检验知,
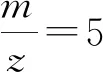

代入得
则5x2-26xy+5y2=0,得x=5y或y=5x,
解得原方程的解为(10,2,3)或(2,10,3).

(河南质量工程职业学院 李永利 467001)
证明设△ABC的半周长为p,
由上式可知,(1)式等价于
(2)
由于(b+c)2-a2=(b+c-a)(b+c+a)>0,
于是(2)式等价于
(b+c)2(2b2+2c2-a2)
≥2(b2+c2)[(b+c)2-a2]
⟺-a2(b+c)2≥-2a2(b2+c2)
⟺(b+c)2≤2(b2+c2)⟺2bc≤b2+c2.
由二元均值不等式b2+c2≥2bc可知上式显然成立,故(2)式成立,从而(1)式成立.
2560⊙O的半径等于等边△ABC的高,且⊙O在BC边上滚动时与AB、AC两边将于E、F,求证:无论⊙O滚到什么位置,△OEF总是等边三角形.

(安徽省淮南三中 王秉春 232007)
证明设⊙O滚到如下图所示的位置,它与BC相切于D点,连结OD、OA,因为OD等于△ABC的高,那么OA∥BC,此时∠OAE=180°-∠ABC=120°,∠OAF=60°.
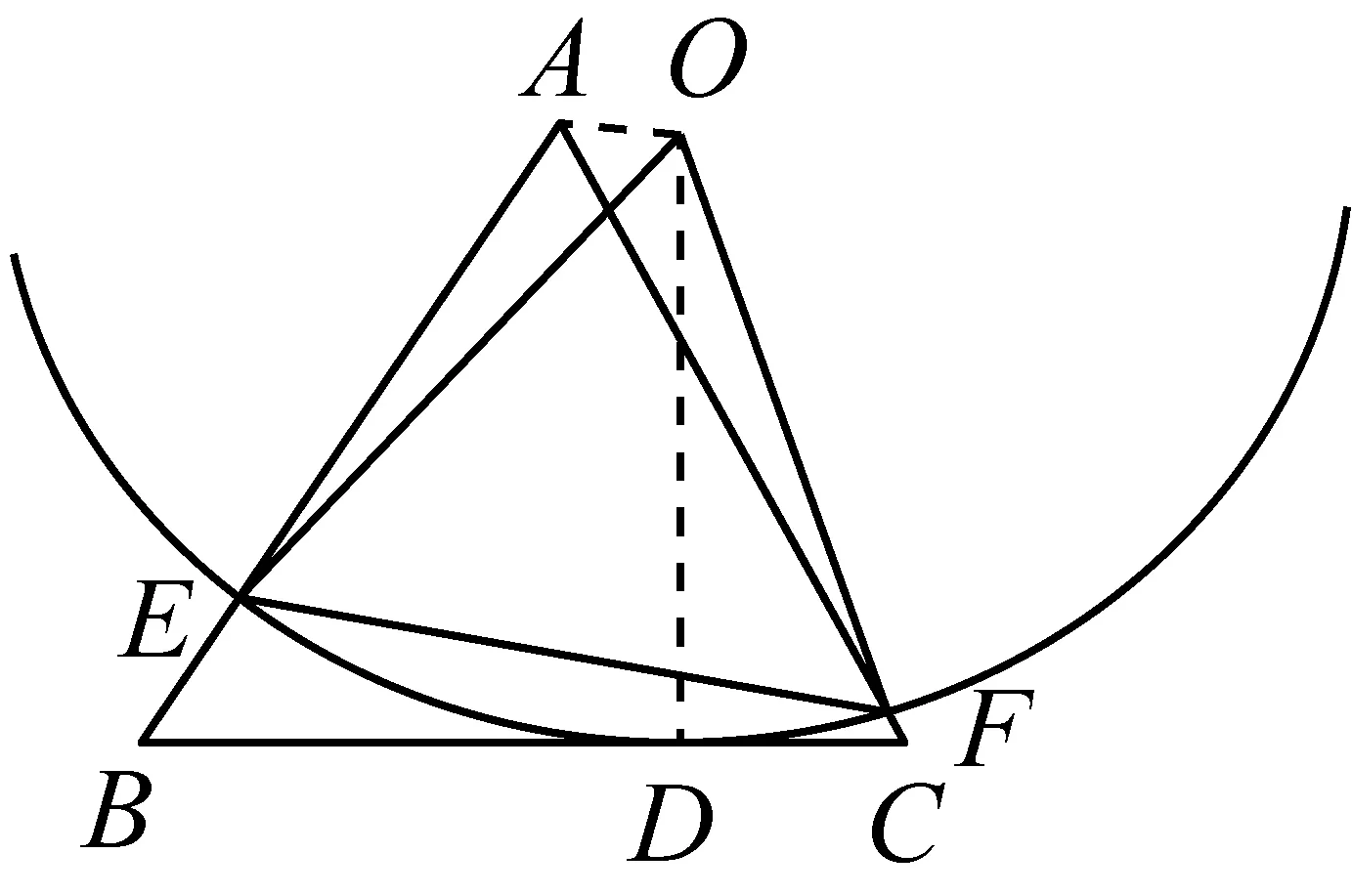
在△OEA中,由正弦定理,得

在△OAF中,由正弦定理,得
因为OE=OF,则sin∠AEO=sin∠AFO.
显然∠AEO、∠AFO都是锐角,∠AEO=∠AFO.那么E、F在线段OA同侧,对OA弦等角,于是A、E、F、O四点共圆.∠EOF=∠EAF=60°,又OE=OF,故△OEF为等边三角形.
2020年9月号问题
(来稿请注明出处——编者)
2561已知(如图),在△ABC中,点D1、D2在BC上,且∠BAD1=∠CAD2.过点D1、D2分别作AC的平行线D1E1、D2E2,与AB分别交于点E1、E2.

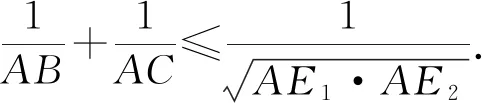
(北京市朝阳区教育研究中心 蒋晓东 100028;北京市朝阳区芳草地国际学校富力分校
郭文征 100121)
2562设a,b,c> 0,且a+b+c=3,证明:
(河南辉县一中 贺基军 453600)
2563△ABC,E、F分别在AB、AC上且EF∥BC交△ABF的外接圆于D,EG∥AC交CD于G,求证:∠ABF=∠CBG
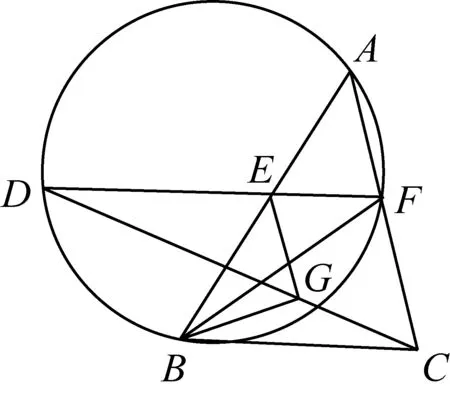
(江西师范高等专科学校 王建荣 335000)
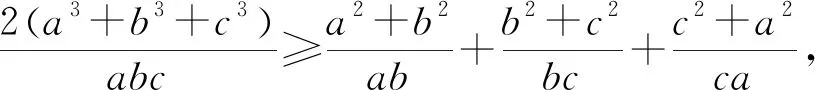
(安徽省太和县第二小学 任迪慧 236630 )
2565如图1,圆上依次有A1、A2、A3、A4、A5五个点,连结A1A3、A3A5、A5A2、A2A4、A4A1,得一五角星,A1A2、A3A4交于A,A1A4、A3A5交于B,若过点A1的圆的切线和A2A5的延长线交于C,则A、B、C三点共线.

图1
(成都市金牛区蜀江路369号2-2-35 张殿书 610036)

